
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лабораторна робота № 5.
|
|
Вивчення конструкції і основних метрологічних характеристик осьових систем теодолітів.
Мета роботи: вивчити конструктивні особливості осьових систем технічних і точних теодолітів, визначити ексцентриситет алідади горизонтального круга теодоліта 3Т2КП.
5.1. Осьові системи теодолітів.
Осьові системи є визначальними для взаємного розташування оптико – механічних вузлів теодоліта. Вони забезпечують збереження необхідних спряжень геометричних осей приладу під час виконання вимірювань, при збереженні і транспортуванні.
За формою осьові системи можуть бути конічними і циліндричними, а за призначенням і розташуванням – вертикальні і горизонтальні.
Деталі вертикальної і горизонтальної осьових систем геодезичних приладів є дуже відповідальними і виготовляють їх з найвищою точністю. Від зазору в осьових парах (вісь - втулка), матеріалу виготовлення, якості механічної та термічної обробки значною мірою залежить точність і довговічність приладу.
Радіальний зазор між спряженими деталями вісь – втулка вертикальної осьової системи становить 0, 0005 – 0, 001 мм, незбіжність осей обертання алідади і горизонтального круга не перевищує 0, 002 мм.
Граничні відхилення від правильної форми мають бути не більшими, ніж 0, 0005 мм. Зазор в осьовій системі є мінімальним, але таким, щоб можливо втримувати шар мастила завтовшки 0, 0005 мм.
Щоб забезпечити легкість ходу та стабільність системи, осі мають бути достатньої довжини. Довжина осі 𝓁, зазвичай у 3 – 4 рази більше її діаметра d, а загалом 𝓁 = 2r, де r – радіус горизонтального круга.
В сучасних геодезичних теодолітах застосовують повторювальні вертикальні системи з поворотним кругом.
На рис.5.1, а подано схему повторювальної системи осей з рухомою втулкою алідади
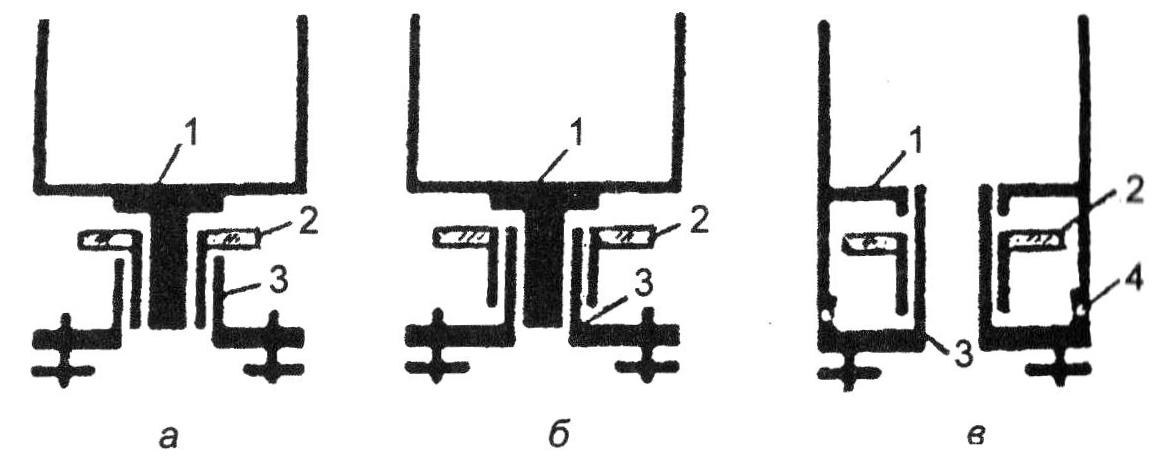
Рис. 5.1, а, б, в. Схеми вертикальних осьових систем: а – повторювальна система осей з рухомою втулкою алідади (система осей Рейхенбаха), б – осьова система з нерухомою втулкою алідади (система осей Борда), в – осьова система, в якої круг і алідада обертаються довкола однієї і тієї самої поверхні нерухомої втулки (система осей Репсольда); 1 – алідада, 2 – круг, 3 – втулка, 4 - розвантажувальні кульки.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Вісь круга 2 обертається у втулці 3 підставки і одночасно є втулкою осі алідади 1. Недоліком цієї системи є ймовірність захоплення та ведення круга алідадою під час її обертання. Таку систему осей використовують звичайно у технічних теодолітах типу Т30, 2Т30, 4Т30. Її називають системою осей Рейхенбаха.
На рис.5.1, б зображено схему вертикальної осьової системи з нерухомою втулкою алідади – система осей Борда. У створі нерухомої втулки 3 обертається вісь алідади 1. Круг 2 обертається довкола зовнішньої поверхні втулки 3. Внутрішня і зовнішня поверхні втулки концентричні. Круг та алідада не дотикаються один до одної, що виключає ймовірність захоплення круга алідадою. Проте система осей з нерухомою втулкою алідади потребує досконалої технології виготовлення, щоб досягти точної концентричної внутрішньої і зовнішньої поверхонь втулки і виключати ексцентриситет алідади і круга. Така система може бути повторювальною з поворотним кругом і застосовується в точних теодолітах типу Т5, 2Т5, Т2, 2Т2 (УОМЗ РФ), Theo 010 (Carl Zeiss Iena) тощо.
Схема вертикальної осьової системи, що має спрощене центрування осей лімба і алідади, наведена на рис.5.1, в і називається системою осей Репсольда. Алідада 1 і круг 2 обертаються довкола однієї і тієї поверхні втулки 3. Тиск від алідадної частини передається периферійно через розвантажувальні кульки 4, тому стабільність осьової системи підвищується. Зазвичай, цю систему з поворотним кругом застосовують у високоточних теодолітах.
Застосування тієї чи іншої осьової системи зумовлено способом вимірювання кута. Наприклад, коли значення вимірюваного кута обчислюють як різницю відліку круга, у такого приладу треба досить нерухомо закріпляти круг на втулці осьової системи.
Під час вимірювання кутів способом повторень кут, що вимірюють, багаторазово послідовно відкладають на крузі. Для цього використовують осьову систему, що дає змогу обертати алідаду як самостійно, так і разом з кругом. Для цього осьова система містить спеціальний, так званий, повторювальний пристрій, який дає змогу легко скрипить круг з алідадою. Теодоліти, в яких передбачена можливість переставляти круг, обладнані пристроєм у вигляді системи зубчастих коліщаток, за допомогою якої можна повертати круг незалежно від інших частин приладу. Це дає змогу виконувати вимірювання способом прийомів, кругових прийомів, в усіх комбінаціях, використовувати щоразу різні ділянки шкали круга, наприклад в точних теодолітах 3Т2КП і 3Т5КП.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Окрім описаного конструктивного поділу, вертикальні осьові системи поділяють за ознаками видів тертя в парах на ти, що мають тертя ковзання, кочення та комбіновані.
Звичайно, досконалішими є два останні типи систем.
В сучасних оптичних теодолітах використовуються циліндричні осі (раніше використовували конусні осі), які сьогодні стали найпоширенішими.
Перед конусними вони мають істотні переваги, а саме: відсутнє навантаження на бічні поверхні осей, не потрібне трудомістке регулювання ходу і часте змащення, осі стабільно працюють впродовж тривалого часу без спеціального догляду.
В циліндричних осях бічна поверхня втулки слугує лише напрямною, а навантаження алідадної частини приладу сприймають упори, підп`ятники, підшипники кочення тощо.
Схеми деяких різновидів конструкції циліндричних осей подано на рис.5.2, зокрема у конструктивної розробці
(рис.5.2, а) навантаження сприймають заплічики,
(рис5.2, б) - сферичний торцевий упор,
(рис5.2, в) – підшипник кочення.
Схеми конкретних конструктивних розробок вертикальних осьових систем теодолітів наведені на рис.5.3.
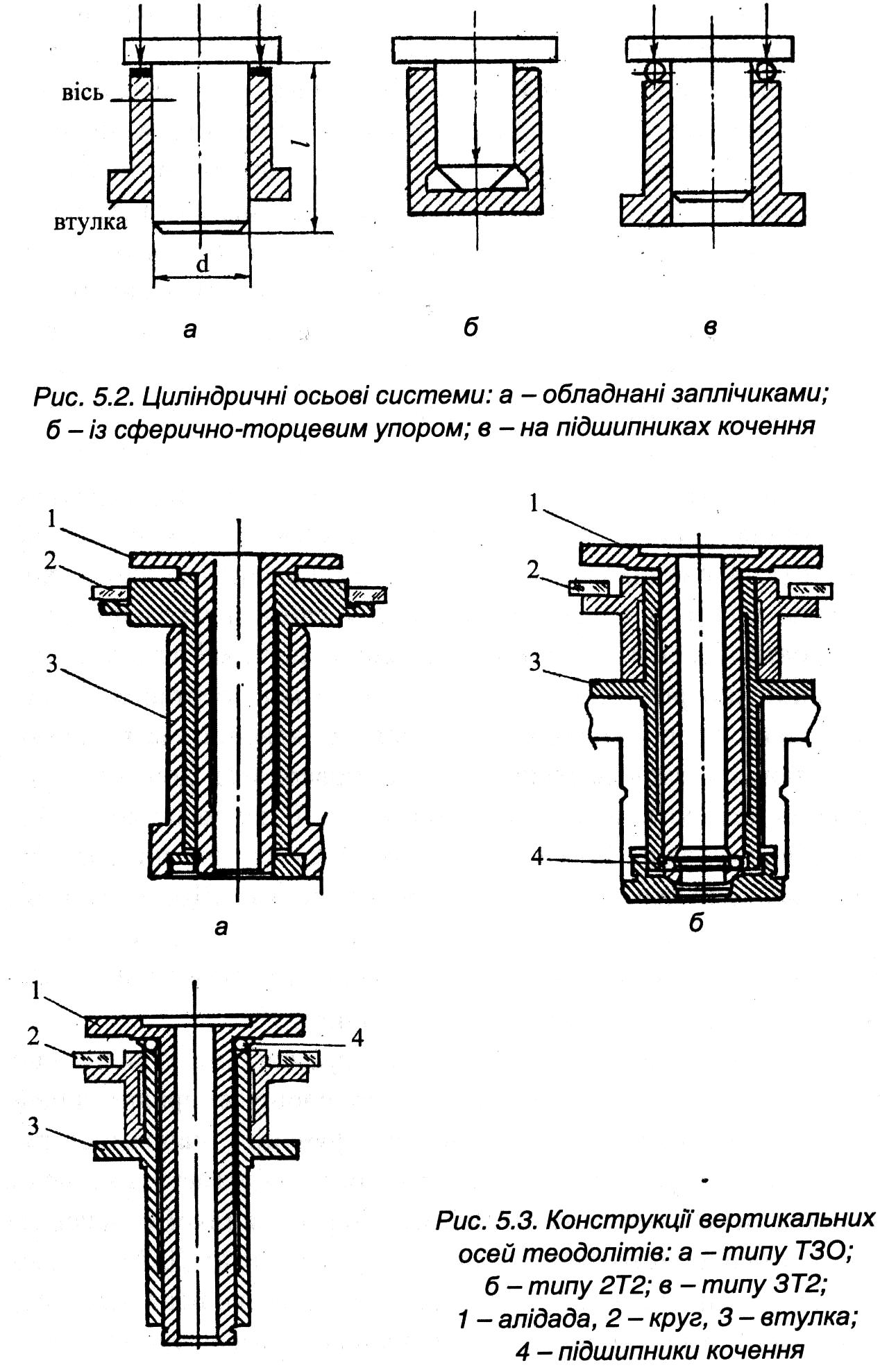
На рис. 5.3, а подано схему вертикальної осьової системи теодолітів типу Т30, 2Т30, 4Т30. Це повторювальна система осей з рухомою втулкою алідади. На рис.5.3, б зображено схему вертикальної осьової системи з нерухомою втулкою алідади теодолітів 2Т2, 2Т5К. Алідадна частина спирається торцем осі алідади на високоточний шарикопідшипник. На помість у теодолітах 3Т2КП, 3Т5КП (рис.5.3, в) у такій самій системі осей застосовано схему розвантаження через кульки у верхній частині осі алідади. Тому схему вважають досить досконалою. Її називають саморегульованою.
Рівномірність і плавність обертового руху вертикальних осьових систем є необхідною умовою точності вимірювань. Конструкція вертикальних осей сучасних приладів та застосування відповідного змащування достатньою мірою забезпечують цю умову. Разом з тим, щоб зменшити площу контакту пари вісь – втулка, зазвичай вдаються до проточування внутрішньої поверхні втулки завглибшки 0, 3 – 0, 5 мм. У результаті вісь та втулка дотикаються одна до одної тільки вузькими поясками.
Наявність необхідного радіального зазору між спряженими деталями вісь – втулка в осьових системах навіть якісного виготовлення спричиняє коливання осей до 2 - 4″ від середнього положення. Застосування осьової системи саморегульованої конструкції викликано необхідністю підвищення точності вимірювань. Опорою алідадної частини у саморегульованій (само центрованій) осьовій системі є сталеві кульки, які встановлені на поверхні, що розташована під кутом до осі обертання алідади. Під дією ваги алідадної частини і власної ваги кульки, намагаючись скочуватися з похилої поверхні донизу, з усіх боків охоплюють вісь, перешкоджаючи її коливанням під час обертання алідади. Внизу вісь дотикається втулки лише вузьким пояском, який керує її рухом у нижній частині. Щоб забезпечити належну стійкість осі під час обертання алідади, різниця діаметрів кульків не повинна перевищувати 0, 0005 мм. У такій осьовій системі коливання не перевищує 1″. Зменшенню коливання осей слугує система з віднесеною опорою на кульки, в якій роз поширено площу спирання алідади. Власне, на вісь поліпшені функції напрямної руху алідади і центрування приладу, проте різниця діаметрів кульків не повинна перебільшувати 0, 0002 мм. Необхідно відзначити, що вертикальні осьові системи теодолітів є найскладнішими за конструкцією відносно інших геодезичних приладів (нівелірів тощо).
Дослідження вертикальних осьових систем дають змогу визначити коливання осі обертання, нахил осі і зазор між спряженими елементами осьової системи. Вимірювання виконують за допомогою рівня, який має ціну поділки не більше від 5″. Рівень закріплюють на алідаді, встановлюють вертикальну вісь приладу прямовисно, а перпендикулярність осі рівня до осі обертання алідади не повинна перебільшувати 0, 5 поділки рівня.
Алідаду переставляють через 30° і фіксують відліки кінців бульбашки рівня у межах двох обертів алідади за напрямком руху годинникової стрілки, а двох у зворотному напрямку. Обчислюють зміну нахилу осі рівня, будують графік відхилень, а за ним визначають величину коливань осі.
Горизонтальна осьова система не тільки за назвою і призначенням, а й за конструкцією відрізняється від вертикальної. Вона слугує для обертання зорової труби. У теодолітах горизонтальна осьова система (рис.5.4, а)
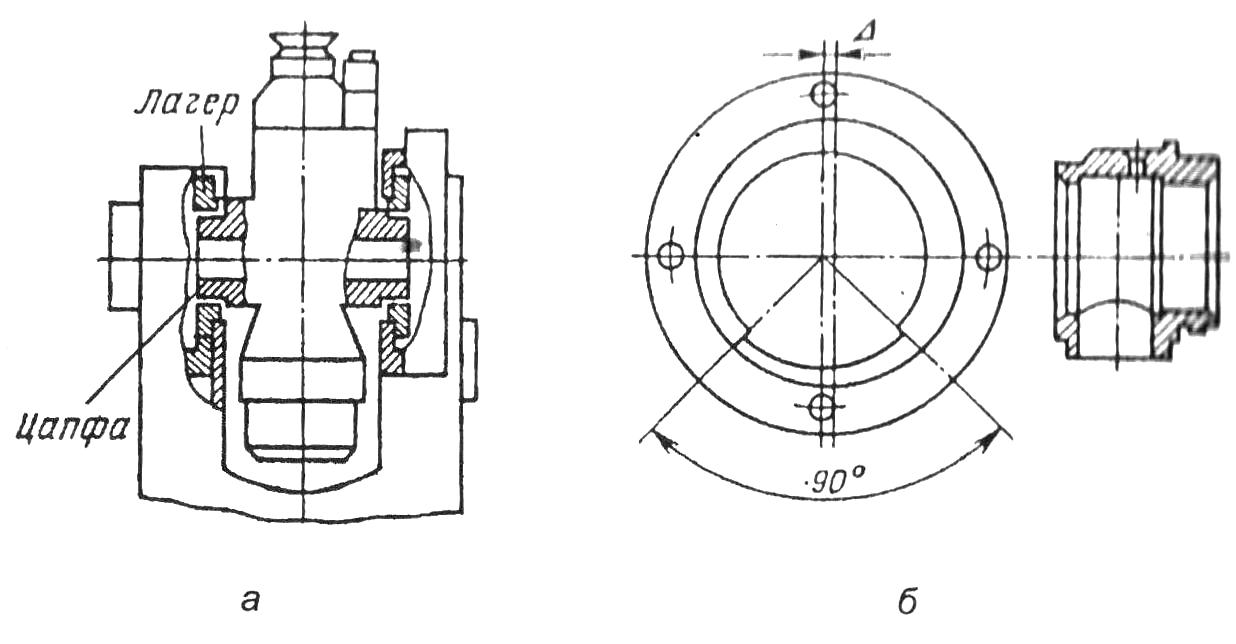
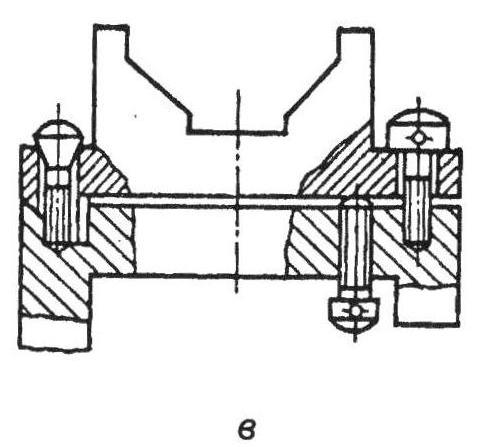
Рис.5.4. Горизонтальна осьова система зорової труби: а – взаємне розташування лагерів та цапф; б – циліндричний лаг ер; в – V– подібний лагер.
складається звичайно з двох циліндричних півосей – цапф, що обертаються у лагерах, які встановлені на вертикальних колонках приладу. Із цапфами жорстко скріплені зорова труба і вертикальний круг. У сучасних теодолітів стійкість горизонтальної осі досягають за рахунок особливостей конструкції лагерів і навідного пристрою. Лагери виконують циліндричними (рис.5.4, а), або V – подібними (рис.5.4, б), конструкція яких містить виправні гвинти. Віддаль між центрами лагерів приблизно дорівнює діаметру вертикального круга. Конструкція циліндричного лаг ера дає можливість робити доволі великим зазор (0.01 – 0, 03) мм між цапфою і лагером. Для того, щоб положення осі було стійким, у нинішній частині лагерів роблять заглиблення 0, 1 – 0, 15 мм, яке обмежене центральним кутом 90° (рис.5.4, б). Вісь отвору лагера зміщена щодо зовнішнього діаметра на величину ∆. Це дає змогу, повертаючи лагери, встановлювати вісь обертання зорової труби перпендикулярно до вертикальної осі приладу.
Конструкція V – подібного лагера (рис.5.4, б) дає змогу змінювати висоту поверхонь спирання цапф за допомогою виправних гвинтів. Навідний пристрій зорової труби конструюють так щоб вплив на вісь сил, які можуть змінювати її азимутальне або висотне положення, був мінімальним. До стабільності горизонтальних осьових систем ставлять такі самі жорсткі вимоги, які до вертикальних. Наприклад, для високоточних теодолітів зміна положення осі обертання зорової труби не повинна перебільшувати 0, 5 - 1″. У зв`язку з цим, відхилення форми цапф осі обертання зорової труби, зокрема, овальність не повинна бути більшою, ніж 0, 001 – 0, 002 мм.
Дослідження горизонтальних осьових систем слугує для визначення відхилення форми цапф від колової циліндричної та нерівності їхніх діаметрів.
Якщо вимірювання на рівній поверхні, на якій невеликі кути нахилу, то досліджувати форму цапф недоцільно, якщо вимірюються кути сторони яких значно відрізняються кутами нахилу, то досліджувати форму цапф доцільно контактним або безконтактним способами.
5.2. Суть визначення ексцентриситету алідади горизонтального круга.
Вісь обертання алідади, центр поділок круга і вісь обертання горизонтального круга в теодоліті мають збігатися.
Проте у зв’язку з неминучою технічною недосконалістю виготовлення і складання деталей та вузлів виникає незбіг осей, який називається ексцентриситетом.
У сучасних точних і високоточних теодолітах лінійна величина ексцентриситету дорівнює декілька мкм.
Ексцентриситетом алідади називають незбіг центра обертання алідади з центром поділок круга.
Ексцентриситетом круга називають незбіг центра обертання круга з центром поділок круга.
Ексцентриситетом осей називають незбіг центрів обертання алідади і круга.
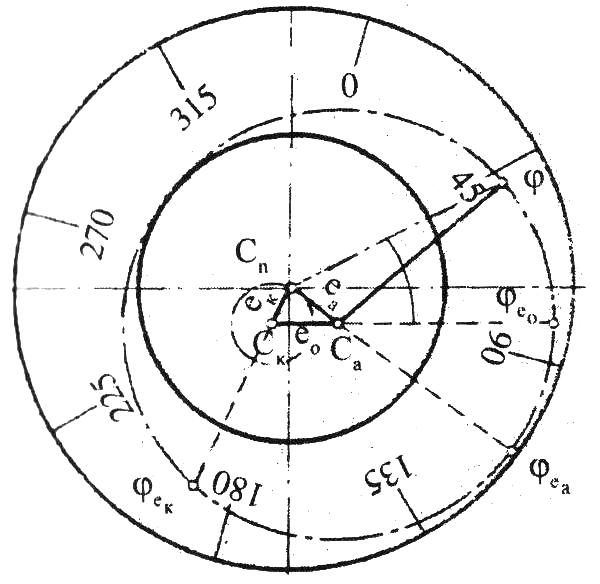
Рис.5.5. Ексцентриситет алідади і горизонтального круга.
На рис.5.5: 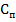 - центр поділок круга,
- центр поділок круга, 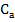 - центр обертання алідади,
- центр обертання алідади, 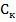 - центр обертання круга.
- центр обертання круга.
Відрізок 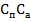 =
= 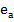 - лінійний ексцентриситет алідади,
- лінійний ексцентриситет алідади,  =
= 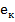 - лінійний ексцентриситет круга,
- лінійний ексцентриситет круга, 
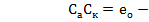 лінійний ексцентриситет осей. Напрямок ексцентриситету характеризують радіуси
лінійний ексцентриситет осей. Напрямок ексцентриситету характеризують радіуси 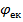 – виражає ексцентриситет круга,
– виражає ексцентриситет круга, 
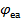 - виражає ексцентриситет алідади,
- виражає ексцентриситет алідади, 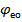 - виражає ексцентриситет осей.
- виражає ексцентриситет осей.
У приладах з одностороннім відлічуванням відлік завжди спотворений впливом усіх ексцентриситетів. У приладів з двостороннім відлічуванням вплив ексцентриситету на відлік виключається, але значний ексцентриситет викликає зміну Рену на різних ділянках круга.
Якщо в теодоліті із двостороннім відлічуванням центр обертання алідади 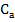 збігається з центром поділок
збігається з центром поділок 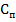 , різниця відліків на діаметрально протилежних ділянках круга буде дорівнювати нулю, тобто
, різниця відліків на діаметрально протилежних ділянках круга буде дорівнювати нулю, тобто
V = 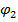 - (
- (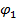 + 180°) = 0. (5.1) Якщо
+ 180°) = 0. (5.1) Якщо 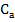 і
і 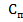 не збігаються, а початки відліків мікроскопу розташовані під кутом
не збігаються, а початки відліків мікроскопу розташовані під кутом 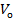 один до одного, різниця від ліків буде дорівнювати
один до одного, різниця від ліків буде дорівнювати
V = 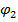 - (
- (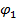 ± 180°) – 2x +
± 180°) – 2x + 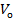 . (5.2) Змінюючи положення алідади на
. (5.2) Змінюючи положення алідади на
σ = 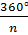 , де
, де 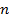 - кількість установлень, одержують
- кількість установлень, одержують 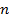 різниць відліку з двох мікроскопів. В теодолітах з двосторонніми відліковими пристроями для визначення V потрібно почергово сумістити зображення двох штрихів з одним і тим самим індексом, відлічуючи шкалу мікрометра.
різниць відліку з двох мікроскопів. В теодолітах з двосторонніми відліковими пристроями для визначення V потрібно почергово сумістити зображення двох штрихів з одним і тим самим індексом, відлічуючи шкалу мікрометра.
Конструкція таких приладів не передбачає наявність у полі зору мікроскопу такого індексу. Тому суміщають зображення одного із цих штрихів зі штрихом вертикального круга. Різниця відліку має величину 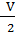 . Кут
. Кут 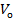 дорівнює куту, під яким індекс розташований до діаметра тих штрихів, які суміщають.
дорівнює куту, під яким індекс розташований до діаметра тих штрихів, які суміщають. 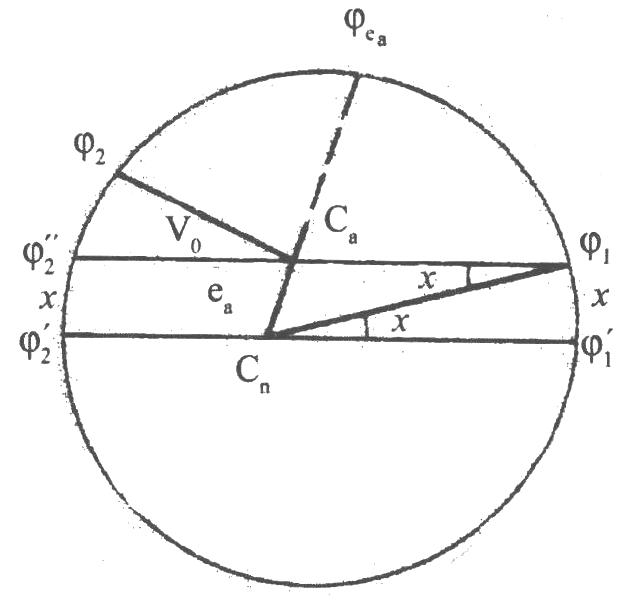
Рис.5.6. До визначення ексцентриситету.
З трикутника 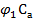
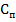 (рис. 5.6.) маємо
(рис. 5.6.) маємо
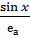 =
= 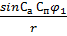 , (5.3) вважаючи, що
, (5.3) вважаючи, що 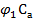 =
= 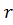 - радіус кругу через малу величину
- радіус кругу через малу величину 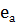 . Якщо кут
. Якщо кут
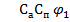 =
= 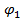 -
- 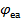 ,
,
де 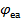 - відлік круга, коли вплив ексцентриситету дорівнює нулю, тобто
- відлік круга, коли вплив ексцентриситету дорівнює нулю, тобто 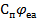 збігається з напрямком лінійного ексцентриситету, то можна записати
збігається з напрямком лінійного ексцентриситету, то можна записати
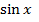 =
= 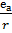
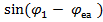 , (5.4) а оскільки
, (5.4) а оскільки 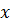 - мала величина, то х =
- мала величина, то х = 
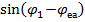 =
=
= 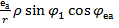 -
- 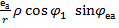 . (5.5) Підставляючи одержане в (5.5) значення x та з рахунком (5.2) маємо
. (5.5) Підставляючи одержане в (5.5) значення x та з рахунком (5.2) маємо
V = 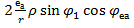 -
- 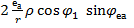 +
+ 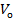 . (5.6) Введемо позначення
. (5.6) Введемо позначення
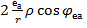 = Х і
= Х і 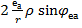 = Y (5.7)
= Y (5.7)
і тоді маємо 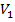 = Х
= Х 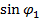 – Y
– Y 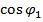 +
+ 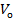 . (5.8)
. (5.8)
Під час дослідження на різних ділянках кругу можна скласти 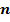 рівнянь виду (5.8), що мають три невідомі Х, Y і
рівнянь виду (5.8), що мають три невідомі Х, Y і 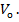 У складі величин V є випадкові похибки вимірювань, тому можна записати умовні рівняння поправок виду
У складі величин V є випадкові похибки вимірювань, тому можна записати умовні рівняння поправок виду
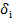 = Х
= Х 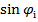 - Y
- Y 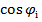 +
+ 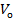 -
- 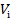 , (5.9)
, (5.9)
де 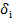 – поправка за похибку різниці відліку V з протилежним знаком.
– поправка за похибку різниці відліку V з протилежним знаком.
Згідно способу найменших квадратів від 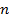 рівнянь поправок (5.9) переходимо до трьох нормальних рівнянь (за кількістю невідомих). Розв’язання цих рівнянь дозволяє отримати
рівнянь поправок (5.9) переходимо до трьох нормальних рівнянь (за кількістю невідомих). Розв’язання цих рівнянь дозволяє отримати
Х = 
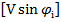 , Y =
, Y = 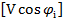 ,
, 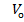 =
= 
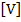 . (5.10)
. (5.10)
Із позначень Х та Y (5.7)
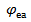 = arc tg
= arc tg  ,
,  =
= 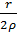
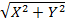 . (5.11) Максимальний вплив ексцентриситету алідади на односторонній відлік круга
. (5.11) Максимальний вплив ексцентриситету алідади на односторонній відлік круга
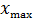 =
= 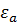 , (5.12)
, (5.12)
а коли 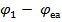 = 90°, тоді згідно із залежністю (5.5)
= 90°, тоді згідно із залежністю (5.5)
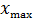 =
= 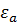 -
- 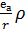 . (5.13) Величину
. (5.13) Величину 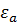 називають кутовим ексцентриситетом алідади, його можна визначити за формулою
називають кутовим ексцентриситетом алідади, його можна визначити за формулою
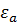 =
= 
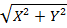 , (5, 14)
, (5, 14) 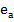 =
= 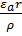 . (5.15) Підставляючи Х, Y,
. (5.15) Підставляючи Х, Y, 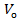 у залежність (5.9) можна визначити значення поправок
у залежність (5.9) можна визначити значення поправок 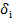 .
.
5.3. Послідовність визначення ексцентриситету алідади горизонтального круга теодоліта 3Т2КП.
Послідовність визначення ексцентриситету алідади горизонтального круга теодоліта з двостороннім оптичним мікрометром наступна. Різниці 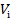 визначають із елементів ексцентриситету, через кожні 30° установлення алідади від 0 до 330° у прямому ході і від 330° до 0° у зворотному ході.
визначають із елементів ексцентриситету, через кожні 30° установлення алідади від 0 до 330° у прямому ході і від 330° до 0° у зворотному ході.
На кожному установленні алідади суміщають діаметрально протилежні штрихи і фіксують відлік А (вільний від ексцентриситету алідади), а потім суміщають штрих горизонтального круга з одним із штрихів вертикального круга, який приймають за нерухомий індекс, і відлічують 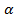 . Щоб побачити вертикальний штрих, повертають рукоятку перемикача кругів на 45°. Тоді у полі зору мікроскопа буде одночасно видно штрихи вертикального круга (наприклад, у верхній половині віконця) і штрихи горизонтального круга (наприклад, у нижній половині віконця).
. Щоб побачити вертикальний штрих, повертають рукоятку перемикача кругів на 45°. Тоді у полі зору мікроскопа буде одночасно видно штрихи вертикального круга (наприклад, у верхній половині віконця) і штрихи горизонтального круга (наприклад, у нижній половині віконця).
Послідовність дій для визначення різниць 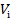 під час кожного установлення алідади, наприклад, першого на 0° така.
під час кожного установлення алідади, наприклад, першого на 0° така.
Маховичком оптичного мікрометра установлюють на шкалі відлік 5′ 00″. Навідним гвинтом алідади суміщають штрихи 0° і 180°. Потім повертають рукоятку перемикача кругів на 45° так, щоб у верхній половині віконця з`явилося зображення штрихів вертикального круга.
Далі навідним гвинтом зорової труби суміщають найближчий штрих вертикального круга з лівим біфілярним штрихом 180° і відлічують горизонтальний круг 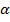 .
.
Зазвичай, суміщення виконують двічі маховичком оптичного мікрометра.
Надалі під час всього дослідження зорова труба залишається нерухомою, позаяк штрих вертикального круга є нерухомим індексом.
Після цього рукоятку перемикача кругів установлюють у положення “ горизонтально “ і установлюють на шкалі мікрометра відлік 5′ 00″.
Повертають алідаду на 30°, суміщають діаметрально протилежні штрихи і далі виконують вже раніше описані дії.
За одержаним відліком визначають коливання
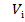 = 4 (5′ 00″ -
= 4 (5′ 00″ - 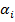 ). (5.16)
). (5.16)
Коливання значення 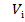 для точних теодолітів не повинні перебільшувати 40″.
для точних теодолітів не повинні перебільшувати 40″.
Для повного уявлення про ексцентриситет алідади, різниці 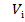 визначають з двох прямих і двох зворотних обертів алідади. Значення
визначають з двох прямих і двох зворотних обертів алідади. Значення 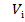 , одержані за формулою (5.16), слугують вихідними даними для обчислення Х, Y,
, одержані за формулою (5.16), слугують вихідними даними для обчислення Х, Y, 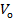 за формулою
за формулою
V =  (
( ), (5.17)
), (5.17)
Х = 
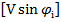 , Y =
, Y = 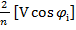 ,
, 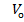 =
= 
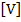 , (5.18)
, (5.18)
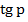 =
= 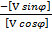 , е =
, е =  ,
, 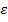 =
= 
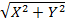 . (5.19)
. (5.19)
Ексцентриситет 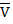 = Х
= Х  + Y
+ Y 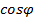 +
+ 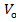 .(5, 20)
.(5, 20)
Результати обчислення склали:
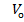
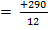 = +24″, Х =
= +24″, Х = 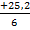 =+ 4, 2″, Y=
=+ 4, 2″, Y= 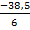 = -6, 4″.
= -6, 4″.
tg p = 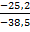 = 0, 656, r = 33°, р= 33°+180°= 216°,
= 0, 656, r = 33°, р= 33°+180°= 216°, 
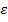 =
= 
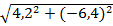 = ±3, 8″, е =
= ±3, 8″, е = 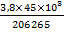 = 0, 83 мкм.
= 0, 83 мкм.
Ексцентриситет 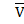 ″ = 4, 2″
″ = 4, 2″  - 6, 4″
- 6, 4″ 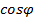 +24″.
+24″.
Таблиця 5.1. Визначення ексцентриситету алідади теодоліта 3Т2КП № 0015. 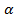 = 5′ 00″, V = 4 (
= 5′ 00″, V = 4 (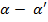 ).
).
| Установка, φ ° | 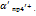 ″ ″
| 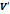
| 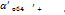 ″ ″
| 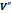
| V | V 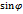
| V 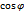
| X 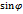
| Y 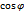
| Ексцентриситет  ″ ″
|
| 0 30 60 90 120 150 180 210 240 270 300 330 | 57 55 54 53 53 51 51 54 55 55 56 56 | +12″ +20 +24 +28 +28 +36 +36 +24 +20 +20 +16 +16 | 56 55 54 53 52 52 50 53 53 54 56 57 | +16″ +20 +24 +28 +32 +32 +40 +28 +28 +24 +16 +12 | +14″ +20 +24 +28 +30 +34 +38 +26 +24 +22 +16 +14 | 0″ +10 +20, 8 +28 +26 +17 0 -13 - 20, 8 -22 – 13, 8 - 7 | +14″ +17, 3 +12 0 -15 -29, 4 -38 -22, 5 - 12 0 +8 +12, 1 | 0″ +2, 1 +3, 6 +4, 2 +3, 6 +2, 1 0 -2, 1 - 3, 6 -4, 2 -3, 6 -2, 1 | -6, 4″ -5, 5 -3, 2 0 +3, 2 +5, 5 +6, 4 +5, 5 +3, 2 0 -3, 2 -5, 5 | +17, 6″ +20, 6 +24, 4 +28, 2 +30, 8 +31, 6 +30, 4 +27, 4 +23, 6 +19, 8 +17, 2 +16, 4 |
| Сума | +290 | +101, 8 | +63, 4 | +288 | ||||||
| -76, 6 | -101, 9 | |||||||||
| +25, 2 | -38, 5 |
По результатах визначення параметрів за виразами (5.17, 5.18, 5.19, 5.20) будують графік змінювання 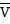 від кута
від кута 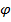 .
.
5.4. Порядок визначення ексцентриситету алідади горизонтального круга теодоліта 3Т5КП.
1-й спосіб визначення включає наступні дії. Теодоліт встановлюємо на тверду основу і приводимо у робочий стан. Установлюємо алідаду на відлік, близький до нуля і, обертаючи лімб, приводимо візирну вісь труби на чітку ціль, яка знаходиться на віддалі 50 -100 м від приладу і приблизно на висоті горизонту інструмента. Беремо відлік на шкалі мікроскопа 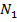 .
.
Переводимо трубу через зеніт і, обертаючи алідаду, знову наводимо візирну вісь труби на ту саму ціль, беремо відлік 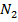 по лімбу. Потім переміщуємо алідаду її навідним гвинтом на декілька хвилин і, повторюючи спостереження, беремо відлік по лімбу
по лімбу. Потім переміщуємо алідаду її навідним гвинтом на декілька хвилин і, повторюючи спостереження, беремо відлік по лімбу 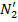 і
і 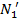 .
.
Після цього установлюємо алідаду на відлік по лімбу близький 30° і, обертаючи лімб, наводимо візирну вісь труби на ту саму ціль. Повторюємо описаний раніше цикл спостережень і відлічуємо 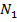 ,
, 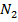 ,
, 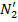 і
і 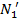 по нерухомому лімбу при двох положеннях труби при К П і КЛ. Далі послідовно переставляємо лімб через 30° по всьому кругу і повторюємо вісь цикл спостережень при відліку, близькому 60°, 90° і т.д. По результатах відлічування обчислимо різниці
по нерухомому лімбу при двох положеннях труби при К П і КЛ. Далі послідовно переставляємо лімб через 30° по всьому кругу і повторюємо вісь цикл спостережень при відліку, близькому 60°, 90° і т.д. По результатах відлічування обчислимо різниці
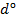 =
=  (
(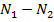 ), (5.21)
), (5.21)
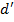 =
=  (
(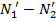 ), (5.22)
), (5.22)
d =  (
(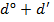 ). (5.23)
). (5.23)
Потім за отриманими різницями обчислимо значення колімаційної похибки С = 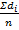 (5.24) і величини ексцентриситету, що незалежні від впливу колімаційної похибки для кожного установлення алідади
(5.24) і величини ексцентриситету, що незалежні від впливу колімаційної похибки для кожного установлення алідади  =
=  (5.25) де n – кількість середніх піврізниць. За значеннями
(5.25) де n – кількість середніх піврізниць. За значеннями 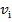 будуємо графік, на якому по осі абсцис відкладаємо значення установлень круга φ, а по осі ординат значення
будуємо графік, на якому по осі абсцис відкладаємо значення установлень круга φ, а по осі ординат значення 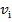 .
.
2-й спосіб визначення включає наступні дії.
Теодоліт встановлюємо на тверду основу і приводимо в робоче положення. На віддалі 20 – 30 м від приладу по колу через 45° або 60° на одній висоті з віссю обертання труби встановлюємо марки. Переставляючи алідаду за напрямом руху годинникової стрілки, при нерухомому положенні лімба, послідовно візуємо трубою при крузі право (К П) на кожну марку і відлічуємо по шкалі мікроскопа.
Переводимо трубу через зеніт і повторюємо вимірювання при крузі ліво (КЛ), знову обертаємо алідаду приладу за напрямом руху годинникової стрілки. Ці вимірювання складають перший прийом. Далі робимо при двох положеннях вертикального круга другий прийом вимірювань, обертаючи алідаду проти руху годинникової стрілки. Для кожного положення алідади знаходимо різниці від - ліків 2 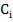 =
= 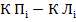 , (5.26) які обумовлені загальним впливом подвійного ексцентриситету 2
, (5.26) які обумовлені загальним впливом подвійного ексцентриситету 2 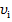 та подвійною колімаційною похибкою 2
та подвійною колімаційною похибкою 2 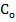 . Потім обчислимо середнє значення подвійної колімаційної похибки 2
. Потім обчислимо середнє значення подвійної колімаційної похибки 2 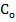 =
= 
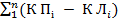 , (5.27)
, (5.27)
де n – кількість установлень алідади. Потім визначаємо величину подвійного ексцентриситету алідади для кожного її установлення за формулою
2 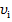 =
= 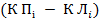 - 2
- 2 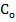 , (5.28)
, (5.28)
і ексцентриситет алідади 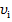 . За значеннями
. За значеннями 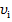 будують графік ексцентриситету алідади горизонтального круга.
будують графік ексцентриситету алідади горизонтального круга.
Таблиця 5.2
| № п/п | Відлік по горизонтальному кругу | 2 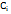 = = 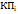 - - 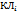
| 2 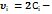 2 2 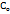
| Ексце- нтриситет 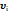
| |
| К П | КЛ | ||||
| Прямий хід | |||||
| 1 2 3 4 5 6 7 8 | 0°02′, 3 45°02′, 7 90°03′, 8 135°02′, 3 180°00′, 4 225°04′, 2 270°01′, 0 315°03′, 2 | 180°02′, 3 225°03′, 2 270°03′, 9 315°02′, 4 0° 00′, 8 45° 04′, 6 90° 01 ′, 8 135°03′, 9 | -0, 6 -0, 5 -0, 1 -0, 1 -0, 4 -0, 4 -0, 8 -0, 7 | - 9″ - 3 +21 +21 +3 +3 -21 -15 | - 4″ - 2 +10 +10 +2 +2 -10 - 8 |
| Сума | -3, 6 | +48 | +24 | ||
2 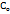 = =  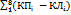 = = 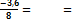 - 0, 45′ = - 27 ″. - 0, 45′ = - 27 ″.
| - 48 | - 24 | |||
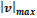 = 0, 5 ( = 0, 5 (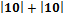 ) = 10″. ) = 10″.
|
Обчислимо також максимальне значення кутового ексцентриситету 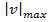 .
.
В теодолітах типу Т5 величини ексцентриситету 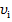 не повинні перевищувати 30″.
не повинні перевищувати 30″.
Приклад визначення ексцентриситету алідади горизонтального круга теодоліта 3Т5КП наведено в табл. 5.2 і на рис. 5.7.
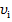 ″
″
| +10 | |||||||
| +5 | |||||||
| -5 | |||||||
| -10 |
0 45° 90° 135° 180° 225° 270° 300° 330° φ °
Рис.5.7. Графік змінювання ексцентриситету алідади горизонтального круга теодоліта 3Т5КП № 0035.
5.5. Порядок виконання лабораторної роботи.
1. Накреслите або зробите ксерокопію схеми вертикальних осьових систем Рейхенбаха, Борда і Репсольда, навидите стислий опис їх особливостей і в яких типах теодолітів вони застосовуються.
2. Накреслите або зробите ксерокопію схеми циліндричних осьових систем, які обладнані заплічиками, сферично – торцевим упором, на підшипниках кочення. Дайте опис їх особливостей і в яких типах теодолітів застосовуються.
3. Накреслите або зробите ксерокопію конструкцій вертикальних осьових систем Т30, 2Т2К і 3Т2КП. Навидите їх стислий опис.
4. Накреслите або зробите ксерокопію схем горизонтальної осьової системи з циліндричним та V – подібним ла - гером. Наведіть стислий опис цих систем.
5. Накреслите або зробите ксерокопію схему видів ексцентриситету горизонтального круга теодоліту та схему впливу ексцентриситету на точність відлічування.
6. Визначите ексцентриситет алідади горизонтального круга теодоліта 3Т2КП або 2Т5К.
7. Дайте висновок про стан осьової системи горизонтального круга теодоліта.
5.6. Контрольні запитання.
1. Які схеми вертикальних осьових систем застосовують в сучасних теодолітах?
2. Які вимоги пред’являють до виготовлення осьової пари (вісь - втулка), до розміру і діаметру осі?
3. Які переваги циліндричних вертикальних осьових систем перед конічними?
4. Які схеми горизонтальних осьових систем застосовують в сучасних теодолітах?
5. Призначення випробувань вертикальних і горизонтальних осьових систем теодолітів?
6. Види і характеристики ексцентриситету горизонтального круга теодоліта?
7. Розповість про порядок визначення ексцентриситету алідади горизонтального круга теодоліта 3Т2КП?
8. Які показники визначають при дослідженні ексцентриситету алідади горизонтального кругу теодоліта?
|
|
