Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Аэродинамические силы .

Все аэродинамические силы, действующие на ракету в полете можно свести к одной результирующей силе R_A, а также к результирующему моменту, действующему относительно масс ракеты.

R_A проходит через точку на продольной оси ракеты, которая носит название центр давления ракеты.

Величина и направление R_A и М_А зависят от ряда факторов, в том числе от 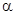, плотности воздуха, скорости воздушного потока, аэродинамической формы ракеты и т.д.

Для того, чтобы было удобно составлять уравнения принято R_A и М_А раскладывать по осям координатной скоростной (поточной) системы.

Известно, что R_A в наибольшей степени, кроме формы ракеты, зависит от угла атаки 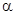и от угла скольжения .

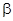§ По осям скоростной системы координат R_A есть:

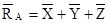
§ По осям связанной системы координат R_A есть:

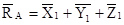
Проекция R_A на поточную ось ракеты Ox_n всегда отрицательна и носит название силы лобового сопротивления ().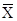

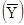- подъемная сила;

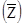- боковая подъемная сила.

Проекция R_A: Х₁ – осевая сила; Y₁ – нормальная сила; Z₁ – боковая нормальная сила.

Баллистическая ракета является аэродинамически осесимметричным телом. Если ось ракеты направлена по вектору скорости (т.е. 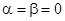), то обтекание ракеты воздушным потоком будет симметричным относительно плоскости, проходящую через продольную ось ракеты, т.е. силы: Y₁=Y=0; Z₁=Z=0.

Если ось ракеты образует с вектором скорости некоторый угол, то обтекание ракеты воздушным потоком будет симметричным относительно плоскости, проходящей через ось ракеты и вектор скорости. При этом R_A и ее составляющие (X, X₁, Y, Y₁) будут лежать в этой плоскости, следовательно что для аэродинамики симметричной ракеты зависимости силы Z(Z₁) от угла скольжения 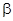аналогичны зависимостям силы Y(Y₁) от угла атаки 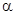. На основании теории аэродинамического подобия проекции аэродинамической силы на оси координат (связанной или скоростной) будут равны.

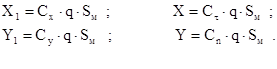, где

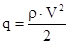- скоростной напор действующий на ракету;

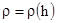- плотность на высоте полета;

V -скорость ракеты;

S_м – характерная площадь ЛА (площадь Миделя);

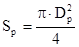; D_p –диаметр цилиндрической части ракеты;

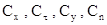- безразмерные аэродинамические коэффициенты.

Аэродинамические коэффициенты зависят от формы ракеты, от ориентации ракеты, относительно вектора воздушной скорости (т.е. от ), а также от критериев аэродинамического подобия.

Критерии аэродинамического подобия:

§ Число Маха ;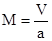

§ Число Рейнольдса ;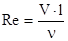

а=а(h) - скорость воздуха в воздушной среде;

l -характерный размер ЛА (для ракеты – длина ракеты);

- кинематический коэффициент вязкости воздуха.