💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Хорда әдісі.

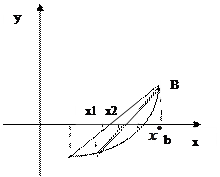
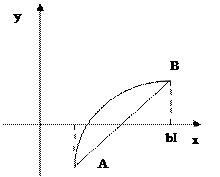
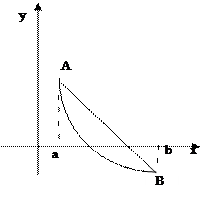
Бұ л ә дістің идеясы [a; b] кесіндісінде F(x) функциясын абсциссалары кесіндінің ұ штары А=a жә не B=b болатын функцияның графигінің нү ктелерін қ осатын хордамен аппроксимациялау (жуық тау) (тө мендегі суретті қ ара):

		II
	I

A

	III
			IV

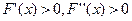
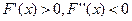
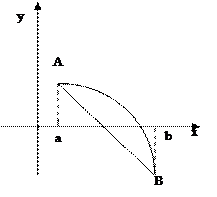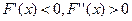
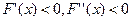
Хорданың абсцисса осьмен қ иылысу нү ктесі тең деудің ізделінуі тү бірдің бірінші жуық мә ні болып табылады. A(a; F(a)) жә не B(b; F(b)) нү ктелерімен ө тетін хорданың тең деуі.

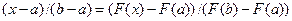
немесе

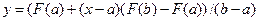(4.1)

Бұ л ө рнектің оң жағ ын 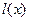арқ ылы белгілеп мына тү рде жазуғ а болады: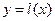

Хорданың тең деуінде у=0 болғ анда оның 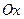осьімен қ иылысу нү ктесінің абсциссасын табамыз:

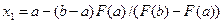(4.2)

F(x) функциясы [a; b] аралығ ында ү зіліссіз, монотонды ө спелі жә не 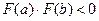болғ андық тан 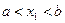. Міне, осылай хорда ә дісі ү шін итерациялық

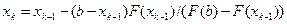(4.3)

формуласын табамыз. Мұ ндай сандық тізбектің шегі (3.1) тең деудің тү біріне жинақ талады. Шынында да, анық болу ү шін 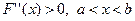делік. Онда функциясы монотонды ө спелі жә не оның графигі ойыс болады. Бұ дан, графиктің ұ штарын қ осатын хорданың ішкі нү ктелері графиктің сә йкес нү ктелерінен жоғ ары орналасады:

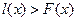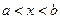, (4.4)

Егер, 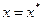тең деудің тү бірі болса, яғ ни 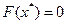, бұ дан 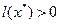екені шығ ады. Ал (4.2) жә не (4.3) тең діктерден алатынымыз:

,

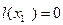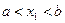
Сонымен,

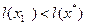(4.5)

Бірақ сызық ты 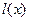функциясы монотонды ө спелі, себебі кесіндінің ұ штарында 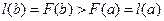сызық тан (4.5) формуладан 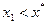тең сіздігі шығ ады. Ә рі қ арай, [a; b] кесіндісін 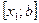кесіндісімен алмастырып жә не 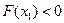екенін ескеріп жоғ арыдағ ыдай тә сілмен 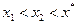екенін анық таймыз. Осылайша индукция бойынша 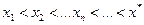екені белгілі. Сонымен 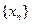тізбегі монотонды ө спелі жә не жоғ арыдан шектелген, демек, ол жинақ ты. Оның шегін 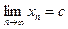деп (4.3) тең діктен шекке кө шіп 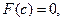яғ ни тізбектің шегі (3.1) тең деудің тү бірі екенін кө реміз.

Дә л осылайша басқ а жағ дайларды да қ арастыруғ а болады.

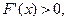
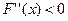(функция ө спелі, графигі дө ң ес),

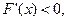
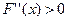(функция кемімелі, графигі ойыс),

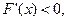
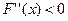(функция кемімелі, графигі дө ң ес),

Ә рбір итерациядан кейін кесіндінің ұ штары қ ысқ арады. Ү зіліссіз жә не дифференциялданатын функцияның қ асиеттеріне байланысты ә рбір рет функция қ арама-қ арсы таң ба қ абылдайтын бө лігі қ алады. Егер 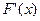жә не 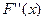бірдей таң ба қ абылдаса, яғ ни 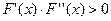(І жә не IV жағ дайлар), онда кесіндінің оң жақ ұ шы x=b қ озғ алмайды жә не 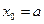деп алынады. Кері жағ дайда, яғ ни 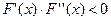болса (ІІ жә не III жағ дайлар), онда сол жақ ұ шы x=a қ озғ алмайды жә не 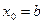деп алынады.

Мысал 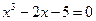тең деуінің [2; 2, 3] кесіндісіндегі тү бірін e=0, 01 дә лдікпен хорда ә дісін пайдаланып табың ыз.

Шешуі: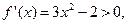

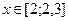
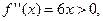
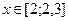
Демек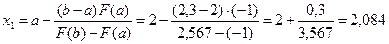

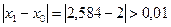
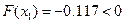
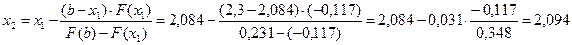
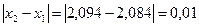
Жауабы: 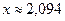.