Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
Жартылай бөлу әдісі.
|
|
Есептің қ ойылыуы. Тең деудің тү бірін табу математикалық мә селесі ғ ылым мен техниканың ә ртү рлі салаларында жиі кездеседі. Бізге келесі тең деулердің тү бірлерін табу керек болсын:
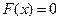 (3.1)
(3.1)
немесе  (3.2)
(3.2)
мұ ндағ ы  жә не
жә не 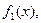
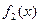 - кейбір
- кейбір 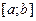 аралығ ында анық талғ ан, ү зіліссіз жә не дифференциялданатын функциялар.
аралығ ында анық талғ ан, ү зіліссіз жә не дифференциялданатын функциялар.
Бұ л тең деулерді
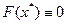 (3.1а)
(3.1а)
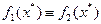 (3.2а)
(3.2а)
тү ріндегі тепе-тең дікке айналдыратын  саны тең деудің тү бірі немесе тең деудің шешімі деп аталады. Егер
саны тең деудің тү бірі немесе тең деудің шешімі деп аталады. Егер 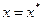 кезінде
кезінде  функциясымен бірге оның
функциясымен бірге оның  -ші ретке дейінгі туындыларының барлығ ы нольге тең болса, онда мұ ндай
-ші ретке дейінгі туындыларының барлығ ы нольге тең болса, онда мұ ндай 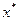 саны k еселі тү бір деп аталады:
саны k еселі тү бір деп аталады:
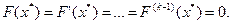
Бір еселі тү бір жай деп аталады. Егер (3.1) тең деудің сол жағ ы тек ғ ана алгебралық функциялар (бү тін, рационал, ироционал) болса, онда (3.1) тең деу алгебралық деп аталады.
Мысалы: 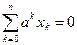 - бү тін алгебралық функция.
- бү тін алгебралық функция.
Ал егер (3.1) тең деудің сол жағ ы алгебралық функция болмаса (логорифмдік, кө рсеткіштік, тригонометриялық жә не т.б), онда ол трансценденттік деп аталады.
Мысалы: 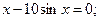

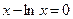 т.б.
т.б.
Сызық ты емес тең деулерді шешудің тура жә не итерациялық ә дістері бар. Тең деуді шешудің тура ә дістері оның шешімін белгілі бір текті қ атынастар (формулалар) арқ ылы ө рнектейді. Мысалы, алгебра курсынан тригонометриялық, кө рсеткіштік, логарифмдік, алгебралық екінші дә режелі 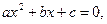 толымсыз ү шінші дә режелі
толымсыз ү шінші дә режелі 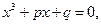 биквадрат
биквадрат  тең деулерінің тү бірлерінің формулалары белгілі. Ә рине, практикада кездесетін тең деулерді мұ ндай қ арапайым ә дістермен шеше беруге мү мкін бола бермейді. Сондық тан қ андай да бір сандық ә дісті пайдалану қ ажеттілігі туады: (3.1) немесе (3.2) тең деуінің [а; b] аралығ ында берілген e дә лдікпен барлық нақ ты тү бірлерін табу керек. Мұ ндай кезде тең деудің тү бірлерін табу ү шін негізінен екі: бө ліктеу (айыру) жә не дә лелдеу кезең інен тұ ратын итерациялық немесе біртіндеп жуық тау ә дістерін қ олданамыз.
тең деулерінің тү бірлерінің формулалары белгілі. Ә рине, практикада кездесетін тең деулерді мұ ндай қ арапайым ә дістермен шеше беруге мү мкін бола бермейді. Сондық тан қ андай да бір сандық ә дісті пайдалану қ ажеттілігі туады: (3.1) немесе (3.2) тең деуінің [а; b] аралығ ында берілген e дә лдікпен барлық нақ ты тү бірлерін табу керек. Мұ ндай кезде тең деудің тү бірлерін табу ү шін негізінен екі: бө ліктеу (айыру) жә не дә лелдеу кезең інен тұ ратын итерациялық немесе біртіндеп жуық тау ә дістерін қ олданамыз.
1) Тү бірлерді бө ліктеу.
def 3.1.  функциясының [a; b] анық талу облысына тиісті ә рқ айсысында (3.1) немесе (3.2) тең деуінің тек бір ғ ана тү бірі болатын
функциясының [a; b] анық талу облысына тиісті ә рқ айсысында (3.1) немесе (3.2) тең деуінің тек бір ғ ана тү бірі болатын 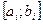 аралық тарына жекелеу тең деудің тү бірлерін бө ліктеу деп аталады.
аралық тарына жекелеу тең деудің тү бірлерін бө ліктеу деп аталады.
Егер тең деудің тү бірі 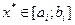 жә не
жә не 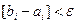 болса, онда
болса, онда
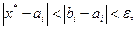

болғ андық тан бұ л аралық тың шекараларын тү бірдің ізделінетін мә нінің e-ге дейінгі дә лдікпен алынғ ан бастапқ ы жуық тауы ретінде алуғ а болады (сол жақ шекарасы кемімен, оң жақ шекарасы артығ ымен). Ә детте тү бірлерді бө ліктеу ү шін функцияның графигін пайдаланады. Ол ү шін, (3.1) тең деудің сол жағ ындағ ы функцияның немесе (3.2) тең деу ү шін 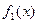 жә не
жә не 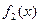 функцияларының [a; b] аралығ ында графиктерін тұ рғ ызамыз. Бірінші жағ дайда
функцияларының [a; b] аралығ ында графиктерін тұ рғ ызамыз. Бірінші жағ дайда 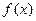 функциясының графигінің абсцисса осімен қ иылысу нү ктесі, екінші жағ дайда
функциясының графигінің абсцисса осімен қ иылысу нү ктесі, екінші жағ дайда 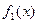 жә не
жә не 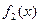 функцияларының графиктерінің қ иылысу нү ктелерінің абсциссалары сә йкес (3.1) жә не (3.2) тең деулерінің жуық мә ндерін береді.
функцияларының графиктерінің қ иылысу нү ктелерінің абсциссалары сә йкес (3.1) жә не (3.2) тең деулерінің жуық мә ндерін береді.
Тү бірлерді айырғ анда кө біне ү зіліссіз жә не диференциялданатын функциялардың қ асиеттерін пайдаланады:
1) Егер [a; b] кесіндінің ұ штарында  функциясыны таң балары қ арама-қ арсы болсын:
функциясыны таң балары қ арама-қ арсы болсын:
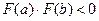 ,
,
онда бұ л аралық та тең деудің тү бірлерінің саны тақ болады, ал егер бірдей таң ба қ абылдаса:
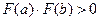 ,
,
онда тү бірлерінің саны жұ п немесе мү лде тү бірі болмайды.
2) Егер 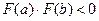 жә не
жә не  немесе
немесе 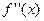 туындылары осы [a; b] аралығ ында таң басын ө згертпесе, онда бұ л аралық та тең деудің бір ғ ана тү бірі болады.
туындылары осы [a; b] аралығ ында таң басын ө згертпесе, онда бұ л аралық та тең деудің бір ғ ана тү бірі болады.
Мысал:  тең деуінің тү бірлерін бө ліктең із.
тең деуінің тү бірлерін бө ліктең із.
|

 1)
1)
 |
 Х Х
| 
| ||
 3 3
| -2 | ||
  2 2
| -3 | ||
          1 1
| -2 | ||
 0 0 | |||
 -1 -1
| |||
 ... ...
| ... |
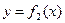
 |
[0; 1], [3; 4]
2)
| X | 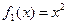
| 
|
| -1 | ||
| -1 | -5 | |
| -2 | -9 | |
| -3 | -13 |
2) Тү бірлерді дә лдеу.
Def 3.2. Бірінші кезең де жекеленген аралық тағ ы тең деудің тү бірі ү шін қ абылданғ ан бастапқ ы жуық тауда берілген e дә лдіктің дә режесіне дейін жеткізуді тү бірді дә лдеу деп атайды, ал пайдаланылатын сандық ә діс итерциялық немесе біртіндеп жуық тау ә дісі деп аталады.
Def 3.3. Егер біртіндеп жуық тауда табылғ ан  мә ндері бірте-бірте тү бірдің дә л
мә ндері бірте-бірте тү бірдің дә л 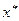 мә ніне жуық тай тү ссе, онда итерациялық процесс жинақ ты деп, ал кері жағ дайда жинақ сыз деп аталады.
мә ніне жуық тай тү ссе, онда итерациялық процесс жинақ ты деп, ал кері жағ дайда жинақ сыз деп аталады.
Итерациялық ә діспен тү бірдің берілген дә лдіктегі жуық мә нін табу ү шін бастапқ ы жуық тау  мә ні жә не қ ажетті дә лдік e берілуі керек. Итерациялық процестің аяқ талу шарты:
мә ні жә не қ ажетті дә лдік e берілуі керек. Итерациялық процестің аяқ талу шарты:
 ,
, 
|
|