
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Реинвестирование (капитализация) процентов
|
|
Пусть на период n установлена процентная ставка i, но при изменении (или без изменения) ставки наращенная к этому моменту сумма вкладывается вновь под простой процент. Такая финансовая операция называется реинвестированием (reinvestment) или капитализацией полученных на каждом этапе наращения средств.
Предположим, что период n1 предшествует периоду n2, который предшествует периоду n3 и т.д. Тогда через время n1 наращенная сумма станет равной величине F1 = P(1+n1i1), после чего будет переоформлена на следующий срок (длительностью n2). Через время n2 наращенная сумма станет равной величине
F2 = F1(1+n1i1) = P(1+n1i1)(1+n2i2) и т.д. Рассуждая аналогичным образом, получим формулу для нахождения наращенной суммы за время n =  при реинвестировании:
при реинвестировании:
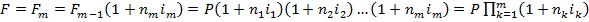 (10)
(10)
Формула (10) приводит нас к схеме сложных процентов.
Пример. Вкладчик поместил в банк 15000 руб. на следующих условиях: в первый год процентная ставка равна 20% годовых, каждые последующие полгода ставка повышается на 3%. Найти наращенную сумму за 2 года, если с изменением процентной ставки происходит одновременно и капитализация процентного дохода.
F = 15(1+0, 2)(1+1/2·0, 23)(1+1/2·0, 26) = 22, 6791 тыс. руб.
|
|
