💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Наращение по учетной ставке

Можно рассмотреть задачу, обратную банковскому дискон­тированию. Пусть от учета капитала F по учетной ставке d за время п была получена сумма Р. Требуется определить вели­чину F. Из формулы (6) получим

(7)

Задачи такого типа возникают, например, при определении суммы, которую надо написать в векселе, если задана текущая величина долга.

Пример. За вексель, учтенный за полтора года до срока по дисконтной ставке 8%, заплачено 2, 2 тыс. руб. Определить номинальную величину векселя.

Поскольку Р = 2, 2; n = 1, 5; d = 0, 08; то из (7) получим

тыс. руб.

Так как , то формула (7) отражает наращение капитала на основе простой учетной ставки d, и приращение I_d капитала вычисляется по формуле

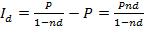(8)

Приращение I_d не пропорционально ни времени n, ни ставке d.

Величина 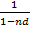является множителем наращения. Этот множитель равен индексу роста капитала Р за время n и явля­ется обратной величиной коэффициента дисконтирования.

При Р = 1 и n = 1 из формулы (8) следует, что

,

т.е. множитель наращения представляет собой сумму, например, рубля и его процентов за один год.

При наращении капитала на основе простой процентной ставки г капитал Р ежегодно увеличивается на одну и ту же величину Р- г. При применении наращения на основе простой учетной ставки d величина начисляемых процентов с каждым годом увеличивается. Пользуясь формулой (8), выпишем в явном виде приращение капитала Р за каждый год.

За первый год (и = 1) капитал увеличится на величину

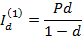
За два года (n = 2) капитал увеличится на величину ,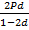

и, следовательно, его приращение за второй год составит:

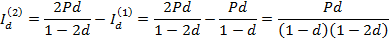
За три года капитал увеличится на величину и, следовательно, его приращение за третий год составит:

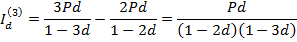
и т.д.

Вообще за k -й год (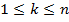) капитал увеличится на вели­чину:

Из написанных равенств следует, что 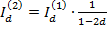, , т.е. , .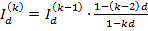

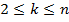И поскольку то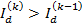

Очевидно, что .

Пример

На капитал в 3 млн. руб. в течение 5 лет осуществляется на­ращение простыми процентами по учетной ставке 12%. Найти приращение первоначального капитала за каждый год и общую

наращенную сумму.

Общая наращенная сумма определяется по формуле (7):

F = = 7, 5 млн. руб. Приращение капитала I_d за пять лет составит величину: I_d = 7, 5 - 3 = 4, 5 млн. руб. Приращения за каждый год равны:

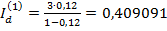млн. руб.

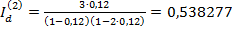м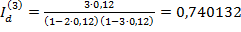лн. руб.

млн. руб.

млн. руб.

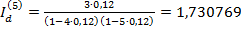млн. руб.

С целью проверки просуммируем полученные величины: 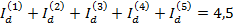млн. руб.,

т.е. как и должно быть, получили I_d.

Формулы (7) и (1) показывают, что простая учетная ставка d дает более быстрый рост, чем такая же по величине простая процентная ставка г.

Формулу (7) можно применять только при n < , так как

при n она приводит к абсурду. Так, при d = 0, 1 и n = 10 (лет) получим F = 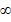, а при n > 10 получим F < 0, что не имеет смысла.

Найдем соотношение между годовыми процентными ставка­ми г и d, обеспечивающими через период времени п получе­ние одной и той же наращенной величины F из начального капитала Р.

Поскольку F=P(1 + nr) и F = 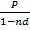, то из равенства P(1 + nr)=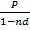

путем несложных алгебраических преобразований получим

d(1 + nr) = r. (9) Пусть n = 1, тогда из (9) следует d(1+r) = r.

Таким образом, ставка r численно равна наращенной сумме, получаемой через год из капитала величиною d, инвестирован­ного под простые проценты г. В свою очередь, d является при­веденной стоимостью величины г, соотнесенной к началу года.

Ставки d и г, связанные между собой соотношением (9), называются эквивалентными, так как они приводят к одинако­вому финансовому результату (выполнение этого требования и позволило получить (9)). Согласно (9) соотношения между процентной ставкой г и эквивалентной ей учетной ставкой d имеют вид:

и

Пример. Найти учетную ставку, эквивалентную простой процентной ставке 19%, при наращении капитала за год. Поскольку n = 1, г = 0, 19, то d = или d 16%. Таким образом, учет за год по учетной ставке 16% приносит такой же доход, как наращение простыми процентами по ставке 19%.

Возможны два способа наращения капитала. В первом случае происходит суммирование первоначального капитала и процентного дохода (в соответствии с процентной ставкой r), причем начисление процентов осуществляется в конце расчетного периода. Такой способ начисления процентов по процентной ставке r называется декурсивным (последующим), а саму ставку r иногда называют ссудным процентом.

Во втором случае проценты начисляются в начале расчетного периода на сумму погашения долга в соответствии с учетной ставкой d. Такой способ начисления процентов называется антисипативным (предварительным). Антисипативное наращение процентов используется, как правило, при учете долговых обязательств, при выдаче ссуд, а также в периоды высокой инфляции.