Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Математическая модель движения РКЛА на свободном участке траектории полета

1.1. Принятые допущения и системы координат

— движение плоское, Земля не вращается;

— принимаем стандартную сферическую атмосферу, гравитационное поле однородное сферическое (атмосфера не зависит от расположения и текущей поры года в месте пуска);

— обтекание корпуса РН симметрично (угол атаки α < < 1);

— корпус РН представляет собой жесткую балку.

Системы координат:

Используем для описания поступательного движения центра масс и определения дальности и высоты полета на АУТ стартовую СК O₀X_g^cY_g^c; для определения текущей скорости полета V скоростную СК O₀X_aY_a.

1.2. Модели атмосферы и гравитационного поля

Опишем состояние атмосферы при помощи параметров стандартной атмосферы:

— давление Р=Р(Н);

— плотность ρ =ρ (Н);

— скорость звука а_∞ (Н);

— где Н – высота полета.

Для поверхности Земли принято значение Н=0:

- Р₀ = 10332 кгс/м²,

- ρ = 0, 125 кгс∙ с²/м⁴,

- а_∞ = 340, 3 м/с,

-Т₀ = 288 °К (15°С).

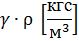
Для произвольной высоты полета на основании таблиц стандартной атмосферы используют следующие зависимости давления и плотности:

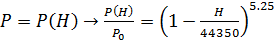, для высот 0 < H ≤ 11км

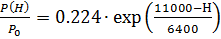, для высот 11км < H ≤ 100 км

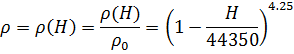
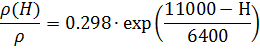
Гравитационное поле:

Используем модель однородного сферического поля. Принимаем, что планета Земля представляет собой шар равномерной плотности ρ _з = const, его объем равен объему реальной Земли (R_шара = 6371, 11 км).

Основной параметр поля – ускорение свободного падения g является функцией высоты полета g=g(H).

Для поверхности Земли:

g₀(H=0)=9.806 м/с²

Для произвольной высоты полета:

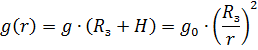
Ускорение g(r) направлено вдоль радиуса к гравитирующему центу (центр Земли).

1.3. Схема сил в полете. Зависимости для сил.

Для представления сил, действующих в полете на АУТ воспользуемся стартовой СК O₀X_g^cY_g^c, связанную OXY и скоростную СК O₀X_aY_a.

Охарактеризуем силы:

1. Сила тяжести :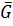

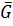=m(t) g(r)

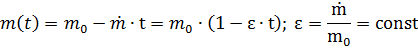
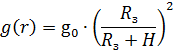
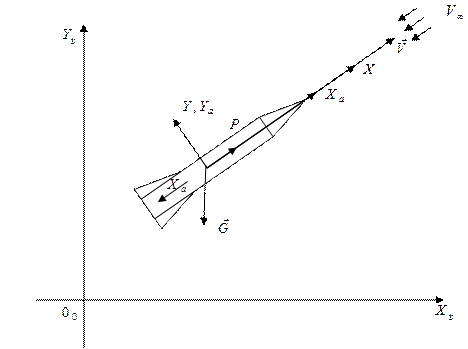
Рис. 1

На рис. 1 показано:

G- сила тяжести;

Р - сила тяги;

Х_а- сила лобового сопротивления.

2. Сила тяги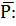

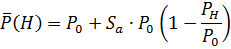
Р₀ – тяга на старте;

S_a – площадь среза сопла.

3. Сила лобового сопротивления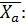

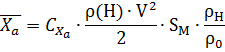
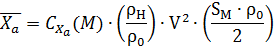
1.4 Уравнение движения на АУТ

1. Запишем динамическое уравнение, характеризующее скорость поступательного движения центра масс РКЛА, проецируя уравнения Мещерского на выбранную систему координат OX_aY_a:

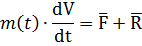
На ось OX_a:

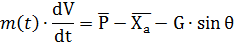
На ось OY_a: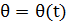

2.Получим кинематическое уравнение дальности и высоты полета РКЛА, проецируя 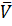на оси O₀X_g^cY_g^c

– дальность

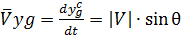– высота

Полученные системы уравнений дополняются зависимостями для функций изменения массы РКЛА

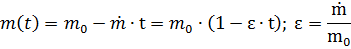
И функциями угла разворота ракеты по тангажу

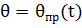
1.5. Выбор программы разворота по углу тангажа

Программой тангажа называют закон изменения угла наклона продольной оси ракеты относительно стартового горизонта.

;

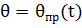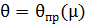
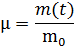
Функция 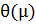должна отображать реализуемую РКЛА форму траектории АУП.

На траектории выделяют следующие подучастки:

- стартовый участок, форма траектории- вертикаль, ,

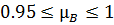
- участок разворота ab, форма- парабола,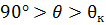

;

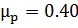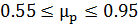
- участок наведения, форма- наклонная прямая,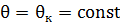

;

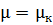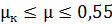
При математическом описании функции разворота 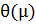вводят ограничения:

- вертикальный старт;

- непрерывность 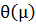и ее производных;

- нулевые углы атаки в диапазоне скоростей полета ;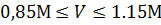

- ограниченные углы скорости разворота корпуса.

Перечисленным ограничениям удовлетворяет функция вида:

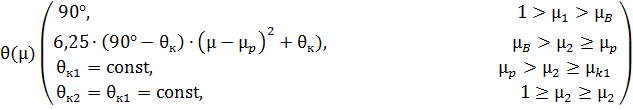
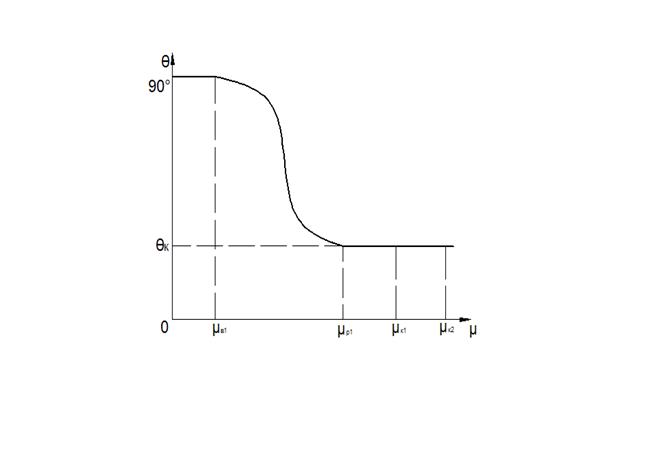
Рис. 2