Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Расчет средней мощности и практической ширины спектра модулирующего сигнала

В соответствие с определением средняя мощность за период T прямоугольной последовательности импульсов выражается через интеграл

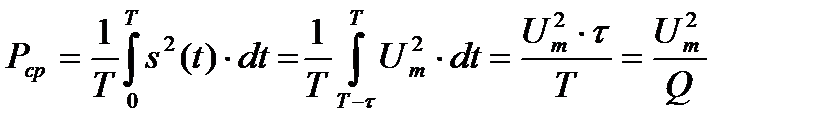, (30)

где 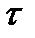- длительность импульса; 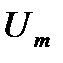- амплитуда; Q - скважность импульсов.

Другой способ нахождения средней мощности заключается в использовании равенства Парсеваля

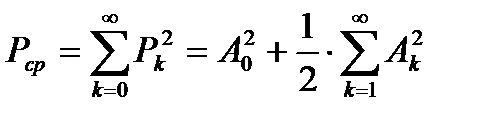, (31)

где 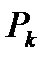- мощности; 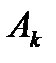- амплитуды гармоник спектра импульсов.

Используя формулы (30), (31), вводят понятие практической ширины спектра. А именно, практической шириной спектра называют такой интервал частот, в котором сосредоточена основная доля мощности, например, 95% от мощности выражаемой формулой (30). Таким образом, чтобы найти практическую ширину нужно суммировать мощности гармоник 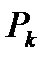в ряде (31) до тех пор, пока, сумма не превысит значений 0.95 от величины мощности в (30). Найденный таким образом наибольший номер 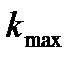гармоники, учтенный в сумме, позволяет вычислить практическую ширину спектра как

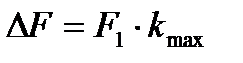, (32)

где 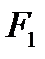- интервал частот между гармониками, равный частоте 1-ой гармоники.

Для рассматриваемого примера варианта задания результаты расчета по формулам (30)-(32), с учетом значений амплитуд гармоник из таблицы 5, имеют вид:

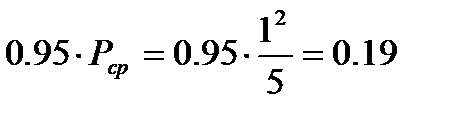Вт

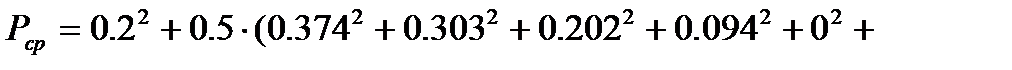
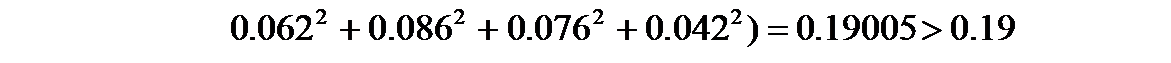
отсюда 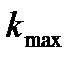= 9 и практическая ширина модулирующего сигнала равна

кГц.