Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Матричная запись квадратичной формы

Матрица

называется матрицей квадратичной формы, ее ранг - рангом квадратичной формы. Квадратичная форма называется невырожденной, если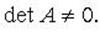

Главные миноры матрицы A называются главными минорами квадратичной формы.

В пространстве 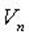квадратичную форму можно записать в виде 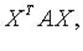где X - координатный столбец вектора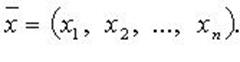

В пространстве 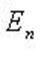квадратичную форму можно представить в виде 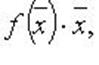где f - линейный самосопряженный оператор, матрица которого в некотором ортонормированном базисе равна A.

Квадратичная форма от переменных 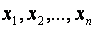будет вполне определена, если заданы ее коэффициенты 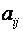, которые составляют матрицу 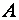. Матрица 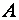называется матрицей квадратичной формы. Она всегда является симметричной. Переменные 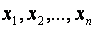могут быть выражены через другие переменные 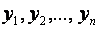. Тогда первый набор называется старыми, а второй - новыми переменными. Если эти наборы связаны формулами

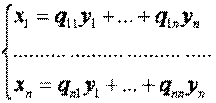(2)

То будем говорить, что задано линейное преобразование переменных с матрицей

(3)

Преобразования, для которых 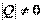, называется невырожденным. Известно, что квадратичная форма от переменных 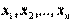с матрицей 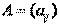при линейном преобразовании (2) с матрицей 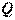преобразуется в квадратичную форму от новых переменных 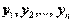с матрицей 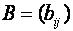, где

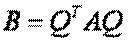
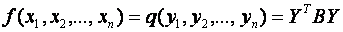(4)