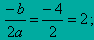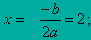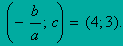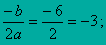Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Различные представления квадратичной функции
|
|
- ВЫДЕЛЕНИЕ ПОЛНОГО КВАДРАТА:

- РАЗЛОЖЕНИЕ НА ЛИНЕЙНЫЕ МНОЖИТЕЛИ
при D > 0 y = ax 2 + bx + c = a (x - x1)(x - x2)
при D = 0 y = ax 2 + bx + c = a (x - x1)2
при D < 0: разложить на множители нельзя
< =" " a=" " > СВОЙСТВА КВАДРАТИЧНОЙ ФУНКЦИИ
- ОБЛАСТЬ ОПРЕДЕЛЕНИЯ: R
- ОБЛАСТЬ ЗНАЧЕНИЙ:
при a > 0 [- D /(4 a); )
)
при a < 0 (- ; - D /(4 a)]
; - D /(4 a)] - ЧЕТНОСТЬ, НЕЧЕТНОСТЬ:
при b = 0, то функция четная
при b 0, то функция ни четная, ни нечетная
0, то функция ни четная, ни нечетная - НУЛИ:
при D > 0 два нуля: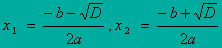
при D = 0 один нуль: x 1 = - b /(2 a)
при D < 0 нулей нет - ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА:

если a > 0, D = 0, то y > 0 при x (-
(-  ; x 1)U(x 1;
; x 1)U(x 1;  )
)
если a > 0, D < 0, то y > 0 при x R
R

если a < 0, D = 0, то y < 0 при x (-
(-  ; x 1)U(x 1;
; x 1)U(x 1;  )
)
если a < 0, D < 0, то y < 0 при x R
R
- ПРОМЕЖУТКИ МОНОТОННОСТИ:


- ЭКСТРЕМУМЫ:
при a > 0 xmin = -b/ (2 a) ymin = -D /(4 a)
при a < 0 xmax = -b/( 2 a) ymax = -D/ (4 a)
< =" " a=" " > НАПРАВЛЕНИЕ ВЕТВЕЙ, ХАРАКТЕРНЫЕ ТОЧКИ И ОСЬ СИММЕТРИИ ПАРАБОЛЫ,
являющейся графиком функции у = ax 2 + bx + c

- Направление ветвей параболы:
при a > 0 ветви направлены вверх
при a < 0 ветви направлены вниз - Координаты вершины параболы: (- b /2 a; - D /4 a)
- Ось симметрии параболы - прямая
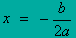
- Точки пересечения (касания) графика с осью х:
D > 0: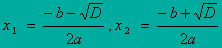 (точки пересечения)
(точки пересечения)
D = 0: x 1 = - b /(2 a) (точка касания)
D < 0: общих точек у графика с осью х нет
- Точка пересечения графика с осью у: (0, c), симметричная ей точка относительно параболы (- b/a; c)
Для построения графика квадратичной функции можно использовать некоторые из указанных характеристик. Например, если уравнение
ax 2 + bx + c = 0 имеет два корня, удобно использовать координаты вершины параболы и координаты двух точек пересечения параболы с осью х.
< =" " a=" " > ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ ПО НАПРАВЛЕНИЮ ВЕТВЕЙ, ХАРАКТЕРНЫМ ТОЧКАМ И ОСИ СИММЕТРИИ ПАРАБОЛЫ
Примеры:
y = x 2 - 4 x + 3
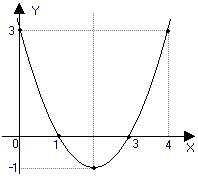
|
|
< =" " a=" " >
y= -x 2 - 6 x - 9
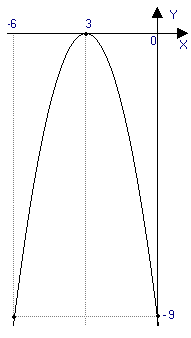
|
|
ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ
С ПОМОЩЬЮ ЭЛЕМЕНТАРНЫХ ПРЕОБРАЗОВАНИЙ ГРАФИКА ФУНКЦИИ
y = x 2
С помощью выделения полного квадрата любую квадратичную функцию можно представить в виде: 
Это свойство позволяет построить график квадратичной функции с помощью элементарных преобразований графика функции y = x 2.
Построение графика y = a (x - m)2 + n можно произвести в три этапа:
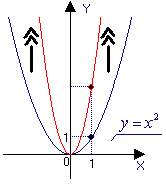
| 1.Растяжение графика y = x 2 вдоль оси у в а раз (при  a a  < 1 - это сжатие в 1/ < 1 - это сжатие в 1/  a a  раз). Если a < 0, произвести ещё и зеркальное отражение графика относительно оси х (ветви параболы будут направлены вниз). Результат преобразования: график функции y = ax 2 раз). Если a < 0, произвести ещё и зеркальное отражение графика относительно оси х (ветви параболы будут направлены вниз). Результат преобразования: график функции y = ax 2
|
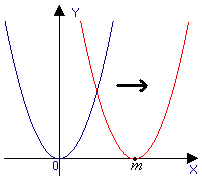
| 2. Произвести параллельный перенос графика функции y = ax 2 вдоль оси x на  m m  (вправо при m > 0 и влево при m < 0). Результат преобразования: график функции y = a(x-m) 2 (вправо при m > 0 и влево при m < 0). Результат преобразования: график функции y = a(x-m) 2
|

| 3. Параллельный перенос графика функции y = a (x - m)2 вдоль оси y на  n n  (вверх при n > 0 и вниз при n < 0) (вверх при n > 0 и вниз при n < 0)
|
Результат преобразования: график функции y = a (x - m)2+ n
Примеры:
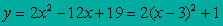
| 
| 
|
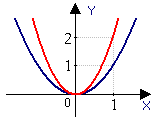
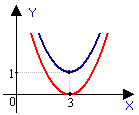
| 1. Растяжение графика функции y = x 2 вдоль оси y в 2 раза | 2. Параллельный перенос графика функции y = 2x 2 вдоль оси x на 3 вправо | Параллельный перенос графика функции y = 2(x - 3)2 вдоль оси y на 1 вверх. |

| 
| 
|
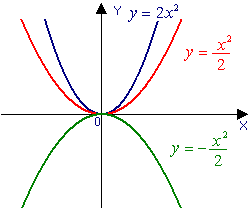
| 1. Сжатие графика функции y = x 2 вдоль оси y в 2 раза и преобразование симметрии относительно оси x | 2. Параллельный перенос графика функции y = - x 2 вдоль оси x на 2 влево | Параллельный перенос графика функции y = - (x + 2)2/ 2 |
|
|