Решения кинетических уравнений некоторых простых и сложных реакций

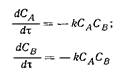
Механизм реакции	Кинетическое уравнение	Решение	Константа скорости

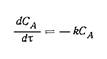
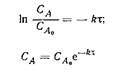
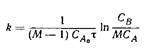
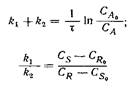
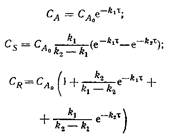
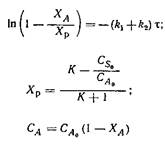
Необходимость решения дифференциальных кинетических урав­нений или их систем возникает чаще всего в одной из следующих задач:

1. Известна схема реакции и величины констант скорости отдель­ных стадий. Требуется рассчитать концентрацию того или иного компонента в некоторый момент времени или установить время, за которое концентрация того или иного компонента достигает опреде­ленного значения. Для этого достаточно найти уравнение кинетиче­ской кривой по интересующему исследователя продукту.

2. Известна схема процесса и опытным путем найдены кинети­ческие кривые компонентов реакции. Необходимо определить кон­станты скорости отдельных элементарных стадий. В этой задаче надо решить дифференциальное уравнение (или систему) в общем виде с константами скорости в качестве параметров, а затем подоб­рать такие значения параметров, которые приводят к совпадению решений с найденными опытным путем кинетическими кривыми.

3. Схема процесса носит гипотетический характер. Требуется установить соотношения между кинетическими характеристиками системы (скоростями, текущими концентрациями, временем), позво­ляющие проверить правильность предложенной схемы. Гипотетиче­ские соотношения выбирают в общем виде с константами скорости в качестве параметров и подставляют в них экспериментальные дан­ные. Если при этом соотношение не оправдывается — схему отвер­гают, как не соответствующую опытным данным, если же соотноше­ние оправдывается, то это является более или менее веским доводом в пользу правильности выбранной схемы.

При решении каждой из перечисленных задач следует сочетать теоретические методы исследований и опытные данные. Третья зада­ча, которая чаще всего возникает при проектировании нового тех­нологического процесса, наиболее трудоемкая и требует использова­ния вычислительных машин. Решение такой задачи является необхо­димой предпосылкой для составления математического описания кинетики проектируемого процесса и построения математической модели реактора.

Особенности гетерогенных процессов

Во всяком гетерогенном процес­се взаимодействие между компо­нентами происходит на поверх­ности раздела фаз или в непо­средственной близости от нее. Гетерогенными системами могут быть: жидкость (газ) – твердое тело; жидкость (газ) – жидкость и др.

Различают некаталитические гетерогенные процессы и катали­тические. К числу некаталитических относятся гетерогенные про­цессы, протекающие как в системе из одного компонента (плавление, кристаллизация, испарение, конденсация, возгонка), так и в систе­мах из двух и более компонентов (растворение, ректификация, ди­стилляция и т. п.). Скорость таких процессов зависит от величины и состояния поверхности раздела фаз (помимо факторов, характери­зующих каждый конкретный процесс). Скорость возрастает при увеличении поверхности и при непрерывном ее обновлении, которое обеспечивается за счет движения.

В гетерогенных каталитических процессах принимает участие катализатор, который, как правило, составляет самостоятельную фазу и оказывает сильное влияние на скорость реакции. Скорость гетерогенных каталитических реакций обычно относят к единице по­верхности раздела фаз:

Во всех процессах гетерогенного катализа реакция протекает на поверхности самого катализатора.

Гетерогенный катализ широко применяется в промышленной практике, при этом наиболее часто встречаются гетерогенные ката­литические системы, в которых взаимодействие компонентов про­исходит на поверхности раздела твердой и газообразной (или жид­кой) фаз. Твердой фазой, обычно, является катализатор. Имеются, конечно, и такие химические процессы, которые протекают либо на поверхности раздела жидкой и газообразной фаз (например, гидро­генизация жидких нефтепродуктов, сатурация, или очистка диффузионного сахарного сока с помощью углекислого газа), либо на поверхности двух жидких фаз (например, нитрование бензола или толуола).

Однако большинство промышленных каталитических процессов осуществляется в гетерогенных системах твердое тело – газ (так называемые газовые каталитические реакции). К числу таких про­цессов относятся:

синтез аммиака, метанола, винилацетата, высших спиртов;

окисление двуокиси серы, этилена, метанола, нафталина;

конверсия метана, окиси углерода и прочее.

На ход гетероген­ных каталитических процессов существенно влияют размеры и при­рода поверхности твердой фазы; характер потока газа (жидкости) у поверхности твердого тела (ламинарный или турбулентный режим); процессы диффузии веществ, которые обусловливают движение реа­гирующих компонентов к твердой поверхности и отвод от нее про­дуктов реакции в газообразную (жидкую) фазу, так называемое транспортирование веществ.

Для гетерогенных систем других типов в целом картина анало­гична, и кинетика гетерогенного каталитического процесса опреде­ляется не только скоростью химического превращения, но и ско­ростью диффузии, которая зависит от типа гетерогенной системы. Следовательно, характерной особенностью гетерогенных химиче­ских процессов является усложнение их явлениями диффузии и в связи с этим в общем случае математическое описание скорости, кроме обычных кинетических уравнений гомогенных реакций, должно содержать еще и выражение массопередачи. Трудность состоит в том, что не может быть одного универсального уравнения скорости, так как выражение массопередачи зависит от типа гетерогенной си­стемы.

На скорость гетерогенного процесса влияет также гидродинами­ческая структура потока или комбинация контактирующих пото­ков. Каждому способу контактирования двух фаз отвечает специ­фическая форма расчетного уравнения и, следовательно, методы расчета гетерогенных систем каждого типа обладают своими харак­терными особенностями.

Общим для всех гетероген­ных систем является то, что кинетическое уравнение описывает результирующую (суммарную) скорость гетерогенного процесса, включающую скорость химического превращения и скорость диффузии. Составляющие суммарной скорости могут иметь близкие зна­чения или резко отличаться друг от друга.

В зависимости от соотно­шения между скоростью химического превращения и скоростью диффузии химические процессы в гетерогенных системах могут проте­кать, либо в кинетической, либо в диффузионной, либо в смешанной области.

Химические процессы, протекающие в кинетической области, характеризуются тем, что скорость собственно химической реакции является наиболее медленной и лимитирует весь процесс, а скорость движения потоков и их физические свойства на процесс не оказы­вают заметного влияния. Для расчета таких процессов могут быть использованы кинетические зависимости без учета влияния диффу­зии, так как кинетика в целом определяется скоростью химическо­го превращения. Условия для возникновения кинетической области создаются при низких температурах, низких давлениях и больших скоростях газового потока.

Для химических процессов, протекающих в диффузионной облас­ти, скорость диффузии реагентов к зоне реакций является лимити­рующей и зависит от скорости движения потоков и их физических свойств. Чтобы рассчитать такие процессы, следует пользоваться зависимостями, характеризующими диффузию, так как кинетика реакции в целом обусловливается скоростью диффузии. В диффузион­ной области скорость процесса сравнительно мало зависит от температуры и практически не зависит от конкретных особенностей химического механизма реакции. Скорости отдельных реакций отличаются лишь постольку, поскольку коэффициенты диффузии реагирую­щих веществ различны. Все реакции в диффузионной области имеют первый порядок по концентрации реагирующего вещества при по­стоянном общем давлении. Условия для возникновения диффузион­ной области создаются при высоких температурах, высоких давле­ниях и малых скоростях газового потока.

Химические процессы в смешанной области протекают при соиз­меримых скоростях химического превращения и диффузии. Здесь уже существенно и одновременное влияние диффузии и кинетики хи­мического превращения, т.е. необходимо находить суммарную скорость процесса. При этом механизм и уравнения скорости гетерогенных каталитических реакций можно выражать через давления компонен­тов реакционной смеси и для описания скорости процесса исполь­зовать концепцию адсорбции и десорбции реагентов и продукта реакции на активных центрах. Подбор уравнений кинетики может производиться несколькими способами, в том числе и при по­мощи вычислительных машин.

Из изложенного выше следует, что понятие лимитирующей ста­дии как стадии, определяющей скорость процесса в целом, имеет важное значение и поэтому исследование кинетики гетерогенных си­стем обычно начинают с установления лимитирующей стадии процес­са. Наиболее просто ее распознают по температурному коэффициен­ту суммарной скорости процесса. Сущность указанного метода состоит в экспериментальном определении суммарной скорости процесса при различных температурах.

Если с изменением температу­ры на 10°С суммарная скорость процесса изменяется в 2÷ 4 раза, то, как следует из уравнения Аррениуса, лимитирующей ста­дией является собственно хими­ческое превращение (кинетиче­ская область). Если же с изме­нением температуры на 10°С скорость процесса изменяется меньше, чем в 1, 8 раза, то ли­митирующим будет массообмен (диффузионная область). В про­межуточных случаях реакция протекает в смешанной (диффузионно-кинетической) области.

Другие методы определения лимитирующей стадии описаны, например, в книгах «Методы кибернетики в химии и химической технологии» - Кафаров В.В.; «Введение в инженерные расчеты реакторов с неподвижным слоем катализатора» - Кафаров В.В. и Михайлов Г.В.

При исследованиях гетерогенных процессов необходимо устано­вить также природу транспортных явлений (перенос вещества и теп­ла), которые неодинаковы для разных типов гетерогенных систем.

В качестве примера приведем гипотезу о влиянии переноса в случае гетерогенной системы твердое тело – газ, в соответствии с которой выделяются такие стадии (см. рис. 8.4):

1) теплообмен и массообмен между внутренней областью части­цы твердой фазы (катализатора) и ее поверхностью;

2) теплообмен и массообмен между наружной поверхностью час­тицы катализатора и потоком газа;

3) перенос тепла и вещества по слою твердой фазы;

4) теплопередача через наружную стенку.

Рис. 8.4. Тепло- и массоперенос в не­подвижном слое катализатора (систе­ма газ – твердое тело).

Механизм процессов, протекающих в гетерогенных системах, отличается сложностью и еще недостаточно изучен, несмотря на существование многих теорий. Первые теоретические работы по хи­мической адсорбции на поверхности твердого тела принадлежат Ленгмюру. Однако расчеты по уравнению Ленгмюра во многих случаях не согласуются с опытными данными, вследствие принятых при его выводе допущений, которые ощутимо искажают реальный процесс.

В настоящее время в разработано несколько тео­рий гетерогенного катализа:

ü теория промежуточных соединений — химическая теория катализа;

ü адсорбционная теория — физическая теория катализа;

ü теория поверхностных промежуточных соединений (Г. К. Боресков, М. И. Темкин, Н. И. Кобозев);

ü мультиплетная теория (Н. Д. Зелинский, А. А. Баландин);

ü теория активных ансамблей (Н. И. Кобозев);

ü электронные теории (Л. В. Писаржевский, С. 3. Рогинский, Ф. Ф., Волькенштейн);

ü цепные теории (Н. Н. Семенов, В. В. Воеводский).

Эти теории все же не являются универсальными, так как каждая из них удовлетворительно объясняет какую-либо сторону сложного процесса катализа, а не весь процесс в целом.

Предпосылки, используемые различными авторами для опреде­ления кинетических уравнений гетерогенно-каталитических реак­ций, значительно отличаются, и до настоящего времени нет единого мнения о пригодности тех или других кинетических моделей.

В инженерных расчетах реакторов с неподвижным слоем катали­затора практический интерес имеют кинетические уравнения, осно­ванные на представлениях Ленгмюра - Хиншельвуда, кинетические уравнения Хоугена - Ватсона, степенная кинетическая модель. Анализ указанных моделей и таблица кинетических уравнений для различных реакций с учетом вида катализатора приведе­ны в книге Кафарова В.В. и Михайлова Г.В. «Введение в инженерные расчеты реакторов с неподвижным слоем катализатора».

Построение кинетических моделей

Как уже отмечалось ранее, уравнения кинетики процесса (кине­тическая модель) являются ос­новой математического описания химического реактора и от точ­ности, с которой они отражают кинетику химического процесса, зависит точность всего последующего расчета реактора и адекватность математической модели. В связи с этим проблеме кинетических моде­лей химических процессов в советской и зарубежной литературе уделяется значительное внимание (работы В. В. Кафарова, М. Г. Слинько, И. И. Иоффе и Л. М. Письмена, В. В. Налимова и Н. А. Черновой, Р. Ариса, С. Вэйласа, О. Левеншпиля и др.).

Для простых реакций установление кинетических уравнений и расчет констант этих уравнений не представляют особых затруднений. При сложных реакциях и, соответственно, сложных урав­нениях с большим числом коэф­фициентов расчет становится тру­доемким, а нередко и невозмож­ным без применения компьютеров.

Обычная процедура составле­ния кинетической модели мо­жет быть изображена следующей схемой (рис. 8.5).

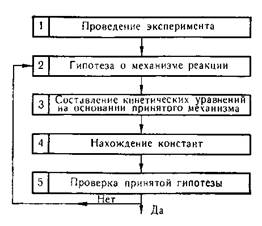
Рис. 8.5. Схема построения кинетической модели

На первом этапе собирают ин­формацию о процессе в ходе опытных исследований (напри­мер, фиксируют изменение кон­центрации исходного вещества во времени), а также анализируют имеющиеся теоретические обобщения. На втором этапе последовательно стро­ят гипотезы о вероятном механизме реакции, исходя из теорети­ческих и экспериментальных сведений о процессе. На третьем и четвертом этапах составляют кинетические уравнения, описы­вающие выбранный механизм реакции, и каким-либо способом определяют значения констант скоростей реакций, которые явля­ются коэффициентами указанных уравнений. Затем по уравнениям находят расчетные кинетические кривые или вычисляют значения кинетических характеристик, соответствующих условиям, при ко­торых проводились эксперименты на первом этапе.

Содержанием пятого заключительного этапа является проверка принятой гипотезы о механизме реакции. С этой целью сравнивают расчетные и экспериментальные данные, полученные на четвертом и первом этапах для одних и тех же условий. Если результаты сравнения неудовлетворительные, т. е. расхождения между расчет­ными и экспериментальными данными недопустимо велики, то следует возвратиться ко второму этапу (выбрать новую гипотезу) и повторять решение задачи до тех пор, пока не будет достигнуто совпадение, удовлетворяющее требованиям данного исследования. Выбор удачной гипотезы зависит как от количества и качества теоретической и экспериментальной информации, так и от опыта ис­следователя.

Наиболее сложным является четвертый этап, поскольку при определении константы скорости реакции нередко возникают су­щественные трудности. В настоящее время известны различные мето­ды установления этого важного параметра, основанные на сочетании эксперимента и теории, которые применяются для нахождения кон­стант скоростей реакций соответствующего типа. В результате проведения экспериментальных исследований и использования соответствующих методов уже сейчас известны достаточно надежные значения констант скоростей для различных химических реакций. Однако еще многие реакции характеризуются малонадежными константами, требующими для их уточнения поста­новки новых измерений, или же вовсе не имеют количественных ха­рактеристик.

Например, в книге В. Н. Кондратьева «Определение констант скорости газофазных реакций» приведены данные о константах скоростей газофазных реакций, кратко изложена сущность приме­няемых в современной кинетике основных экспериментальных ме­тодов определения констант скорости элементарных химических про­цессов и дана критическая оценка результатам исследований оте­чественных и зарубежных ученых в этой области. В числе современ­ных методов в указанной книге рассмотрено также применение вычислительной техники, для определения вероятных значений констант скорости реакций и приведены соотношения, найденные при помощи ЭВМ, по которым вычисляются вполне надежные значения констант.

Отметим, что моделирование химической кинетики на ЭВМ и постановка математического эксперимента позволяют выяснить мак­симальное количество информации о процессе. При этом можно уста­новить, во-первых, варианты механизмов реакций, которые согла­суются с результатами экспериментального исследования процесса и, во-вторых, значения параметров, описывающих данный механизм реакции.

Задача определения кинетических констант сложной реак­ции обычно формулируется как задача поиска минимума функции многих переменных (предэкспонент, энергий активации и др.). Подобную экстремальную задачу можно решать различными спо­собами. Опыт показывает, что эффективными при этом являются методы нелинейного программирования. Большой объем вычисле­ний и нелинейность функций при решении таких задач требуют применения для разработки кинетических уравнений (этапы 4 и 5) компьютеров и современного программного обеспечения.

Задания для самостоятельного решения

1. Как взаимосвязаны между собой реальные скорости образования и расходования отдельных участников реакции
aA + bB → rR + sS?

2. Что такое частный порядок реакции по компоненту A_i? Как взаимосвязаны частные порядки по разным компонентам и общий порядок реакции?

3. Запишите уравнение Аррениуса в дифференциальной, интегральной и логарифмической формах. В чем суть уравнения С. Аррениуса?

4. Определите энергию активации реакции, если при изменении температуры от 450 до 500°С ее скорость возрастает в 2, 73 раза.

5. Две параллельные реакции

a₁A + b₁B → rR + sS (целевая реакция)

a₂A + b₂B → yY + zZ (побочная реакция)

характеризуются следующими кинетическими уравнениями:

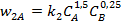
Энергии активации реакций равны Е1 = 45 кДж/моль, Е2 = 65 кДж/моль, соответственно. Проанализируйте зависимость дифференциальной селективности для такой системы реакций: а) от концентрации реагента А; б) от концентрации реагента В; в) от температуры. Какие можно дать рекомендации по выбору технологического режима для этого процесса на основе проведенного анализа?