
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
При протекании реакции окисления аммиака.
|
|
Данные полученные в соответствии со стехиометрическими уравнениями (8.1), (8.2) –
штриховые линии; экспериментальные данные полученные в соответствии со схемой превращения (8.5) – сплошные линии
Тщательное изучение кинетики и механизма реакции показало, что реальное изменение концентрации NO и N2 несколько иное, оно представлено сплошными линиями на том же рисунке. Анализ полученных графических зависимостей показывает, что содержание NO сначала увеличивается, а затем уменьшается. Значит, наряду с его образованием в соответствии с уравнением (8.1) в реакционной смеси происходит дальнейшее превращение NO. Действительно, кроме реакций (8.1), (8.2) имеют место следующие превращения:
2NO = N2 + O2; (8.3)
6NO + 4NH3 = 5N2 + 6Н2O. (8.4)
Схема превращения показывает реальные взаимодействия между компонентами – пути превращения – в реагирующей системе. Она может быть представлена системой химических уравнений протекающих реакций подобно уравнениям (8.1 ÷ 8.4) или графически:
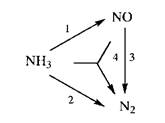 (8.5)
(8.5)
Схема превращения состоит из частных реакций, или этапов. В отличие от стехиометрических, кинетические уравнения не могут быть записаны произвольно, и их число должно соответствовать реальным путям превращения компонентов.
Как видно из приведенного примера, схема превращения необходима в предсказании и объяснении динамического изменения содержания веществ в реагирующей системе по мере протекания в ней химических превращений.
Скорость превращения и скорость реакции
В химической технологии используют два показателя скорости химического процесса – скорость превращения вещества и скорость реакции.
Скорость превращения вещества wi определяется количеством вещества, превращающегося в единицу времени в единице реакционного пространства:
| wi = | Количество превращенного i -го вещества | = | Δ Ni | = | dNi |
| Промежуток времени · Объем реакционного пространства транства | Δ t· V | dt· V |
Реакционным пространством является объем, за исключением тех случаев, когда превращение происходит на границе раздела фаз. Тогда реакционным пространством считается поверхность.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Для исходных компонентов wi < 0 (вещество расходуется), для продуктов
wi > 0 (вещество образуется).
Из уравнения для простой реакции, представленного в алгебраической форме

вытекает постоянство соотношения между количеством Δ Ni – превращенных веществ и их стехиометрическими коэффициентами. Напомним: (Ni - Ni, 0) / vi = n – полнота реакции – постоянна для всех компонентов простой реакции. Продифференцировав и разделив на значение реакционного объема, получим
dNi /(dt·V· vi) = wi / vi.
Это соотношение называется скоростью реакции
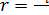 (8.6)
(8.6)
Необходимо отметить, что знак скорости превращения i - вещества зависит от того расходуется оно или образуется в результате реакции, а скорость реакции всегда положительная величина. Очевидно, что скорость превращения любого участника реакции, исходя из скорости реакции
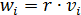 (8.7)
(8.7)
Если реакция сложная и вещество участвует в нескольких частных реакциях, то
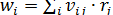 (8.8)
(8.8)
где rj – скорость j -ой реакции.
Как и константа равновесия, величина скорости реакции зависит от формы записи реакции. Например, реакцию синтеза аммиака можно записать:
N2 + 3Н2 = 2NH3
либо
0, 5N2 + 1, 5Н2 = NH3
Если скорость образования аммиака wNH3 будет количественно однозначна, то скорости реакции, определенные по первому или второму уравнению по формуле (8.6), будут различаться в два раза: в первом уравнении реакции vNH3 = 2 и vNH3 = 1 – во втором.
Данная зависимость кинетической характеристики процесса от способа записи стехиометрического уравнения делает некорректным такое определение скорости реакции. Однако в химической технологии это оправдано. Во-первых, в задачу технологических расчетов входит определение изменения количества каждого компонента химической реакции. Соответственно, определяющими параметрами являются wi. Во-вторых, в экспериментальных исследованиях кинетики реакции скорость превращения контролируют по скорости превращения одного из веществ, т.е. опять по величине wi. Поэтому использовать строгое определение скорости реакции, которое приведено в учебниках о кинетике химических превращений, в технологических расчетах неудобно. На практике, определяя величину скорости реакции, сначала записывают ее уравнение, а затем используют уравнение (8.7) или (8.8) для расчета скорости превращения любого компонента.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Нередко скорость реакции определяют по изменению концентрации одного из компонентов во времени r = dC/dt. Но это не всегда применимо, так как в этом случае определение скорости реакции связано с определенным веществом. С другой стороны, концентрация вещества может меняться не только в результате его превращения, но и вследствие изменения объема реагирующей смеси. А когда в реакционный сосуд непрерывно подают исходные вещества и непрерывно выводят соответствующее количество продуктов, как это часто организовано в производстве, то концентрация вещества не будет меняться во времени. Но реакция протекает! Таким образом, уравнение r = dC/dt показывает связь между скоростью превращения и изменением концентрации вещества только в закрытом сосуде, т.е. позволяет рассчитать скорость реакции в таком процессе, но не является ее определением.
Кинетическое уравнение реакции
Скорость реакции во многом зависит от условий ее протекания, главным образом, от температуры и концентрации (парциальных давлений) компонентов. На скорость реакции в каталитических процессах влияет также природа и концентрация катализатора, на скорость фотохимических реакций – интенсивность излучения и т.д.
Кинетическое уравнение, или кинетическая модель, реакции – зависимость скорости реакции от условий ее протекания.
Формы кинетических уравнений весьма разнообразны. Методы построения кинетических моделей и способы определения ее параметров являются предметом специального раздела физической химии.
Для простой элементарной реакции А + В = R + …, т.е. протекающей в одну стадию, кинетическое уравнение строится на основе закона действующих масс:
r = k·CA·CB (8.9)
где: k - константа скорости реакции; СА, СB – концентрации компонентов А и В.
Отметим, что закон действующих масс применим строго только к элементарной реакции, в которой взаимодействие компонентов происходит в одну стадию. Большинство реакций – сложные по механизму и состоят из ряда последовательно-параллельных взаимодействий (стадий). В общем виде кинетическое уравнение представляется в виде
r = k·f(Ci), (8.10)
в котором на скорость реакции влияют все компоненты реакции.
При протекании сложной реакции количество кинетических уравнений вида (8.10) будет равно количеству частных реакций в общей схеме превращения.
В кинетическом уравнении (8.10) k – константа скорости реакции, зависимость которой от температуры и энергии активации описывается уравнением Аррениуса:
k = k0·e -E/RT (8.11)
где k0 – предэкспоненциальный множитель, связанный с вероятным числом соударений; Е – энергия активации.
Из уравнения следует, что чем больше величина энергии активации Е, тем значительнее увеличивается k с ростом температуры. Это соотношение нужно для оценки влияния температуры на скорость разных реакций проходящих в изучаемой системе.

Рис. 8.2. Влияние величины энергии активации Е реакции на изменение
константы скорости реакции k при изменении температуры Т
Например, две реакции охарактеризованы энергиями активации Е1 и Е2, причем Е1 > Е2 и с увеличением температуры скорости обеих реакций возрастают. Соотношение (8.11) позволяет сделать вывод, что с увеличением температуры будут возрастать и скорости реакций, но для реакции с энергией активации Е1 это возрастание будет больше (рис. 8.2).
Кинетическое уравнение вида (8.10) описывает скорость простой необратимой реакции (или частной необратимой реакции в сложной схеме превращения).
Простая обратимая реакция А = R фактически представляет собой сложную, в которой протекают два частных превращения: А превращается в R - прямая реакция; и R превращается в А - обратная реакция. Скорость реакции r будет равна разности скоростей прямой r+ и обратной r- реакций: r = r+ - r-.
Допустим, что обе реакции имеют первый порядок:
r+= k+CA (8.12)
r- = k-CR (8.13)
Тогда,
 (8.14)
(8.14)
В полученном уравнении перед квадратной скобкой стоит выражение скорости прямой реакции.
При равновесии r+ = r- и, следовательно,
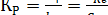 (8.15)
(8.15)
Подставим (8.12) (8.15) в уравнение (8.14)
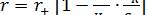 (8.16)
(8.16)
Более того, можно показать, что скорость любой обратимой реакции можно представить в таком виде
 (8.17)
(8.17)
Принимая во внимание температурные зависимости k+, k- и KP
k+ = k+0·e –E+/RT; k- = k-0·e –E- /RT; КР = kР0·e QP/RT
получим:

т.е. тепловой эффект обратимой реакции равен разности энергий активации обратной и прямой реакций. Это фундаментальное соотношение представлено на диаграмме рис. (8.3).
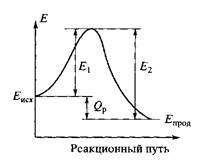
Рис. 8.3. Изменение энергетического потенциала
реагирующей системы Е по пути реакции
Кинетические уравнения некоторых химических превращений
Кинетические модели могут представлять очень сложные зависимости, которые можно построить на основе механизма реакции. Однако в большинстве случаев зависимость скорости реакции от концентрации реагентов выражается степенным законом (закон действующих масс)
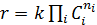 (8.18)
(8.18)
где Сi – концентрации исходных реагентов; ni – порядок реакции по данному компоненту (показатель степени при концентрации i -го реагента); Ʃ ni = n – общий порядок реакции, т.е. сумма порядков реакции по всем реагирующим веществам, он определяет характер зависимости скорости от концентрации.
Следует подчеркнуть, что степенная зависимость от концентрации реагирующих веществ практически всегда выполняется для скоростей отдельных стадий химического процесса. При этом как порядок по отдельному веществу, так и суммарный порядок реакции всегда являются целыми положительными числами. Если речь идет об отдельной стадии процесса, то порядок ее никогда не превышает трех. Поэтому особое значение, в химической кинетике, имеют реакции первого, второго и третьего порядка. В общем случае суммарный порядок сложной реакции может быть нулевым, дробным либо целым числом. Обычно он определяется экспериментально.
|
|
