
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
Порядок решения задачи
|
|
1. Найти приближенное решение задачи с шагами 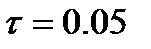 и h =0.01, используя
и h =0.01, используя
явную разностную схему. Построить графики решений при значениях
t = 0.5  , 20
, 20  , 200
, 200  .
.
2. Используя результаты задачи 2.1, экспериментально определить момент времени t, при котором происходит установление процесса (визуально).
3. Произвести анимацию процесса установления.
4. Исследовать, как влияет начальная температура на процесс установления, взяв другие функции 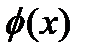 (согласованные с граничными условиями).
(согласованные с граничными условиями).
ПРИЛОЖЕНИЕ 2.A
Схема вариантов к ЛР 1.2.
| N | Выполняемые задачи | N | Выполняемые задачи | N | Выполняемые задачи |
| 2.1.1, 2.2.1, 2.4.1, 2.5.1, 2.6.1 | 2.1.11, 2.2.6, 2.4.11, 2.5.11, 2.6.11 | 2.1.21, 2.2.11, 2.4.21, 2.5.21, 2.6.21 | |||
| 2.1.2, 2.3.1, 2.4.2, 2.5.2, 2.6.2 | 2.1.12, 2.3.6, 2.4.12, 2.5.12, 2.6.12 | 2.1.22, 2.3.12, 2.4.22, 2.5.22, 2.6.22 | |||
| 2.1.3, 2.2.2, 2.4.3, 2.5.3, 2.6.3 | 2.1.13, 2.2.7, 2.4.13, 2.5.13, 2.6.13 | 2.1.23, 2.2.12, 2.4.23, 2.5.23, 2.6.23 | |||
| 2.1.4, 2.3.2, 2.4.4, 2.5.4, 2.6.4 | 2.1.14, 2.3.7, 2.4.14, 2.5.14, 2.6.14 | 2.1.24, 2.3.12, 2.4.24, 2.5.24, 2.6.24 | |||
| 2.1.5, 2.2.3, 2.4.5, 2.5.5, 2.6.5 | 2.1.15, 2.2.8, 2.4.15, 2.5.15, 2.6.15 | 2.1.25, 2.2.13, 2.4.25, 2.5.25, 2.6.25 | |||
| 2.1.6, 2.3.3, 2.4.6, 2.5.6, 2.6.6 | 2.116, 2.3.8, 2.4.16, 2.5.16, 2.6.16 | 2.1.26, 2.3.13, 2.4.26, 2.5.26, 2.6.26 | |||
| 2.1.7, 2.2.4, 2.4.7, 2.5.7, 2.6.7 | 2.1.17, 2.2.9, 2.4.17, 2.5.17, 2.6.17 | 2.1.27, 2.2.14, 2.4.27, 2.5.27, 2.6.27 | |||
| 2.1.8, 2.3.4, 2.4.8, 2.5.8, 2.6.8 | 2.1.18, 2.3.9, 2.4.18, 2.5.18, 2.6.18 | 2.1.28, 2.3.14, 2.4.28, 2.5.28, 2.6.28 | |||
| 2.1.9, 2.2.5, 2.4.9, 2.5.9, 2.6.9 | 2.1.19, 2.2.2, 2.4.19, 2.5.19, 2.6.19 | 2.12.9, 2.2.15, 2.4.29, 2.5.29, 2.6.29 | |||
| 2.1.2, 2.3.5, 2.4.2, 2.5.2, 2.6.2 | 2.1.20, 2.3.2, 2.4.20, 2.5.20, 2.6.20 | 2.1.30, 2.3.15, 2.4.30, 2.5.30, 2.6.30 |
Таблица к задаче 2.1
| № | k(x) | f(x) | a | UA | b | UB |
| 2.1.1 | 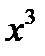
| 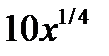
| ||||
| 2.1.2 | 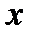
| 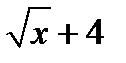
| 0.5 | 1.5 | ||
| 2.1.3 | 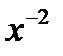
| 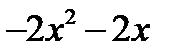
| 0.5 | 1.5 | ||
| 2.1.4 | 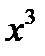
| 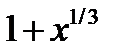
| 0.2 | 1.2 | ||
| 2.1.5 | 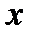
| 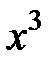 +2 +2
| 0.1 | 1.1 | ||
| 2.1.6 | 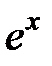
| 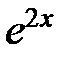
| 0.5 | 1.5 | ||
| 2.1.7 | 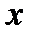
| 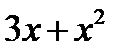
| ||||
| 2.1.8 | 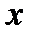
| 
| 0.1 | 0.8 | 0.6 | |
| 2.1.9 | 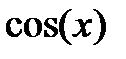
| 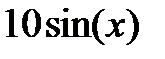
| 0.1 | 0.8 | ||
| 2.1.2 | 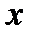
| 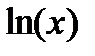
| 0.1 | 0.6 | ||
| 2.1.11 | 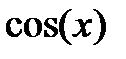
| 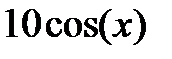
| 1.5 | |||
| 2.1.12 | 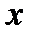
| 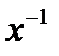
| ||||
| 2.1.13 | 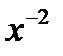
| 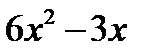
| -2 | 2.2 | ||
| 2.1.14 | 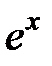
| 
| 2.5 | -2 |
Окончание таблицы к задаче 2.1
| 2.1.15 | 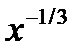
| 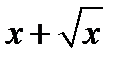
| 1.5 | 2.5 | -3 | |
| 2.1.16 | 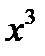
| 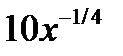
| 0.1 | 1.1 | ||
| 2.1.17 | 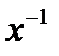
| 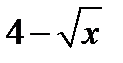
| 1.5 | -2 | 2.5 | -4 |
| 2.1.18 | 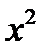
| 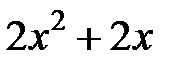
| 0.5 | 1.6 | ||
| 2.1.19 | 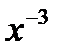
| 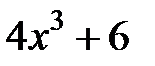
| 0.2 | 1.2 | ||
| 2.1.20 | 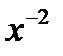
| 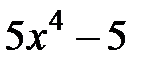
| 1.5 | -1 | 2.5 | |
| 2.1.21 | 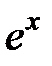
| 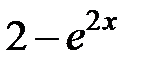
| 0.3 | -1 | 2.3 | |
| 2.1.22 | 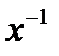
| 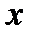
| ||||
| 2.1.23 | 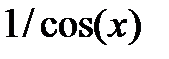
| 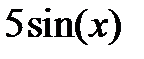
| 0.5 | 1.5 | ||
| 2.1.24 | 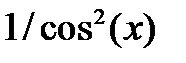
| 
| 0.5 | 1.3 | ||
| 2.1.25 | 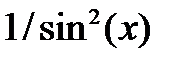
| 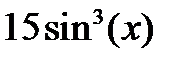
| 0.2 | -1 | 1.2 | -1 |
| 2.1.26 | 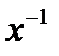
| 
| 0.3 | 2.3 | ||
| 2.1.27 | 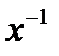
| 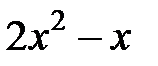
| -4 | |||
| 2.1.28 | 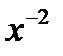
| 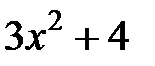
| 1.2 | -4 | 2.4 | |
| 2.1.29 | 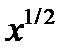
| 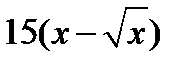
| 0.5 | 1.5 | ||
| 2.1.30 | 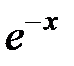
| 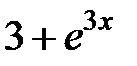
| 0.3 | 2.3 |
Таблица к задаче 2.2
| № | p(x) | q(x) | f(x) | a | b | UA | UB | 
|
| 2.2.1 | 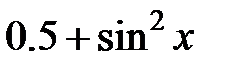
| 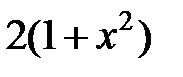
| 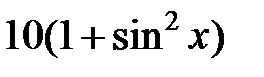
| 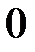
| 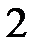
| 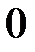
| 
| 0.02 |
| 2.2.2 | 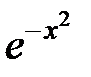
| 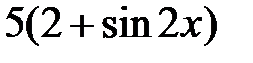
| 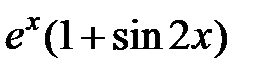
| 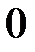
| 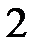
| 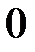
| 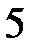
| 0.05 |
| 2.2.3 | 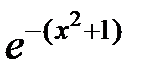
| 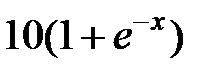
| 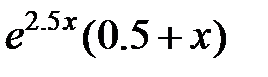
| 
| 
| 
| 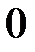
| 0.03 |
| 2.2.4 | 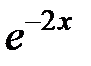
| 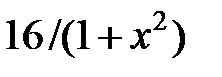
| 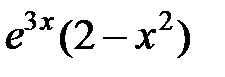
| 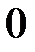
| 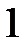
| 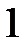
| 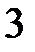
| 0.05 |
| 2.2.5 | 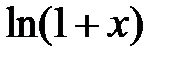
| 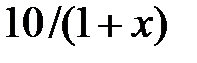
| 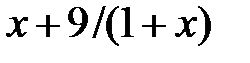
| 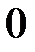
| 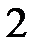
| 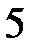
| 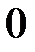
| 0.01 |
| 2.2.6 | 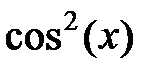
| 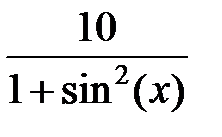
| 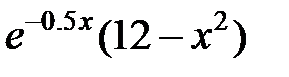
| 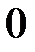
| 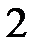
| 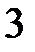
| 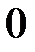
| 0.05 |
| 2.2.7 | 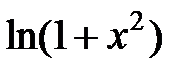
| 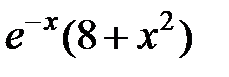
| 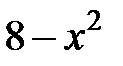
| 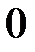
| 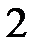
| 
| 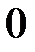
| 0.01 |
| 2.2.8 | 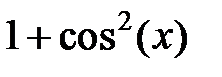
| 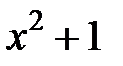
| 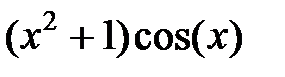
| 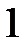
| 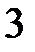
| 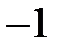
| 
| 0.05 |
| 2.2.9 | 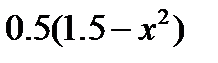
| 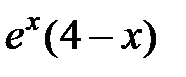
| 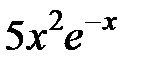
| 3.5 | 0.02 | |||
| 2.2.2 | 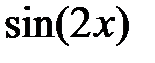
| 
| 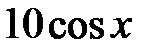
| 0.05 | ||||
| 2.2.11 | 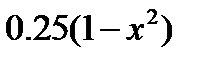
| 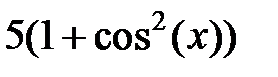
| 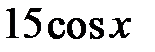
| 0.02 | ||||
| 2.2.12 | 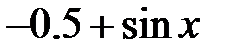
| 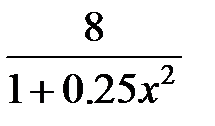
| 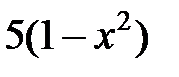
| 0.01 | ||||
| 2.2.13 | 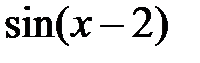
| 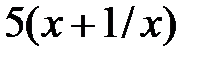
| 0.04 | |||||
| 2.2.14 | 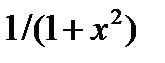
| 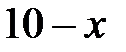
| 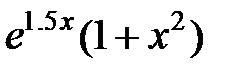
| 0.05 | ||||
| 2.2.15 | 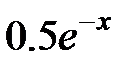
| 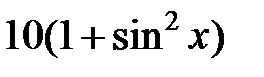
| -1 | 0.02 | ||||
| 2.2.16 | 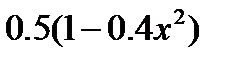
| 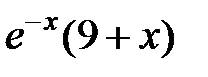
| 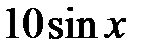
| 1.5 | 0.03 | |||
| 2.2.17 | 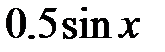
| 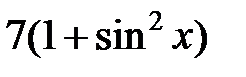
| 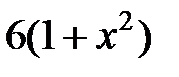
| 0.05 | ||||
| 2.2.18 | 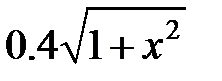
| 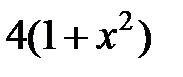
| 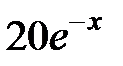
| 2.5 | 0.05 | |||
| 2.2.19 | 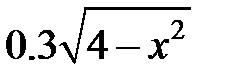
| 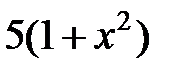
| 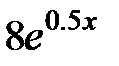
| -1 | 0.1 | |||
| 2.2.20 | 
| 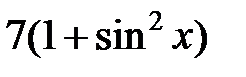
| 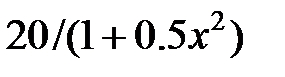
| 1.5 | -1 | 0.005 | ||
| 2.2.21 | 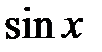
| 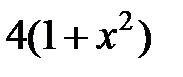
| 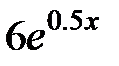
| 0.05 | ||||
| 2.2.22 | 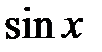
| 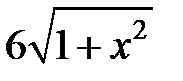
| 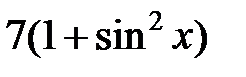
| 0.05 | ||||
| 2.2.23 | 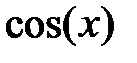
| 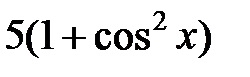
| 
| 1.5 | 0.05 | |||
| 2.2.24 | 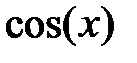
| 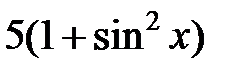
| 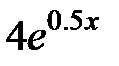
| 0.02 | ||||
| 2.2.25 | 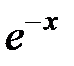
| 
| 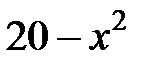
| 0.01 | ||||
| 2.2.26 | 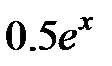
| 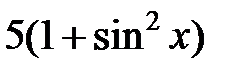
| 0.02 | |||||
| 2.2.27 | 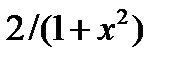
| 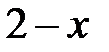
| 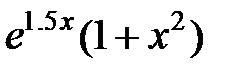
| 0.05 | ||||
| 2.2.28 | 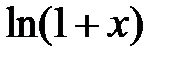
| 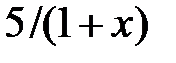
| 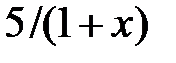
| 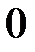
| 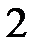
| 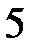
| 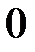
| 0.05 |
| 2.2.29 | 
| 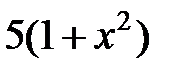
| 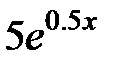
| 0.2 | ||||
| 2.2.30 | 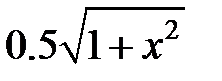
| 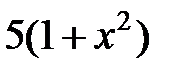
| 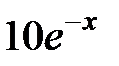
| 2.5 | 0.2 |
Таблица к задаче 2.3
| № | Задача | 
| № | Задача | 
|
| 2.3.1 | 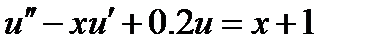
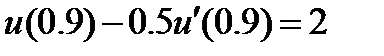
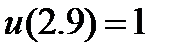
| 0.04 | 2.3.11 | 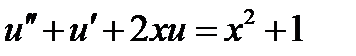

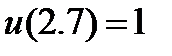
| 0.03 |
| 2.3.2 | 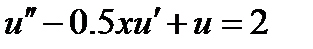
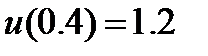
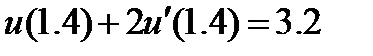
| 0.005 | 2.3.12 | 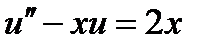
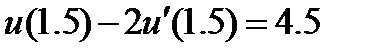
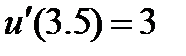
| 0.1 |
| 2.3.3 | 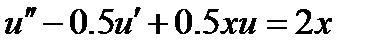
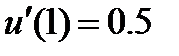
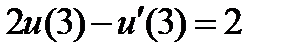
| 0.05 | 2.3.13 | 
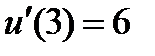
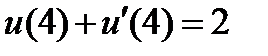
| 0.1 |
| 2.3.4 | 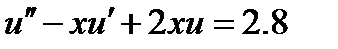
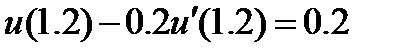 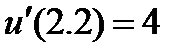
| 0.07 | 2.3.14 | 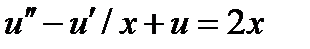
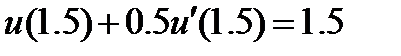 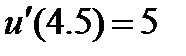
| 0.05 |
| 2.3.5 | 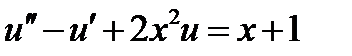
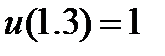
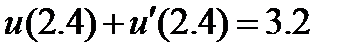
| 0.1 | 2.3.15 | 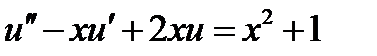
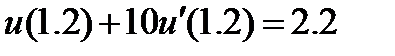
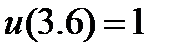
| 0.03 |
| 2.3.6 | 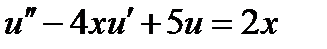
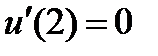
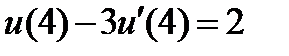
| 0.07 | 2.3.16 | 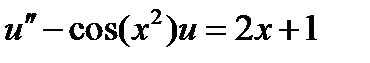

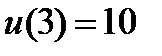
| 0.02 |
| 2.3.7 | 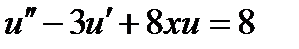
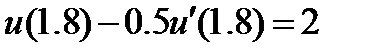
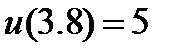
| 0.1 | 2.3.17 | 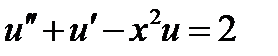
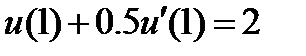
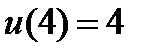
| 0.02 |
| 2.3.8 | 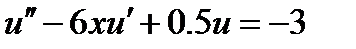
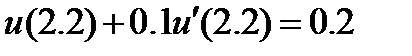
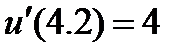
| 0.03 | 2.3.18 | 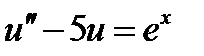
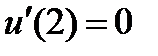
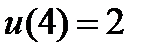
| 0.2 |
| 2.3.9 | 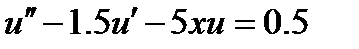
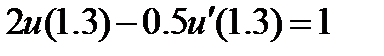
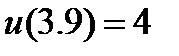
| 0.05 | 2.3.19 | 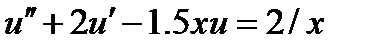
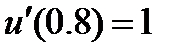
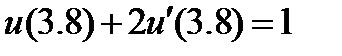
| 0.1 |
| 2.3.2 | 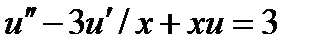
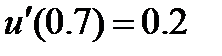
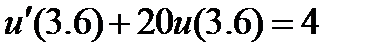
| 0.03 | 2.3.20 | 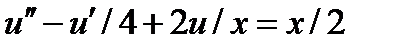
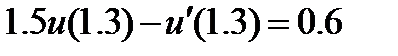
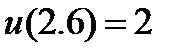
| 0.03 |
Таблица к задаче 2.5
| № | a | b | c | k(x) | q (x) | f (x) | ||
| a< x< c | c< x< b | a< x< c | c< x< b | |||||
| 2.5.1 | 1.5 | 1.125 | 0.5 | 1.4 | 3.2 | 8.5 | 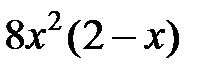
| |
| 2.5.2 | 1.8 | 1.275 | 0.4 | 1.4 | 3.2 | 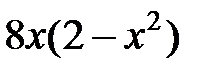
| ||
| 2.5.3 | 2.0 | 1.515 | 0.5 | 1.8 | 3.5 | 8.2 | 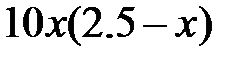
| |
| 2.5.4 | 2.3 | 1.875 | 0.4 | 1.8 | 3.5 | 12.8 | 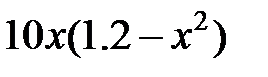
| |
| 2.5.5 | 2.5 | 1.875 | 1.2 | 0.5 | 8.3 | 3.5 | 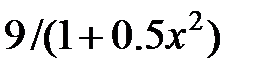
| |
| 2.5.6 | 2.8 | 1.875 | 1.2 | 0.4 | 8.3 | 2.8 | 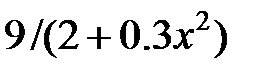
| |
| 2.5.7 | 3.0 | 1.875 | 1.5 | 0.6 | 8.3 | 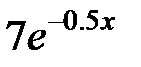
| ||
| 2.5.8 | 1.5 | 0.925 | 1.5 | 0.4 | 7.5 | 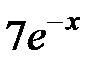
| ||
| 2.5.9 | 1.7 | 0.925 | 1.8 | 0.4 | 7.0 | 
| ||
| 2.5.2 | 1.125 | 1.8 | 0.6 | 6.5 | 7.8 | 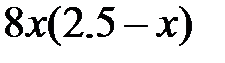
| ||
| 2.5.11 | 2.2 | 1.125 | 0.5 | 1.8 | 3.5 | 7.8 | 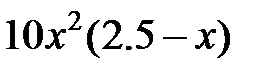
| |
| 2.5.12 | 2.5 | 1.515 | 0.3 | 1.8 | 3.5 | 8.3 | 
| |
| 2.5.13 | 2.7 | 1.815 | 0.5 | 1.2 | 5.6 | 12.3 | 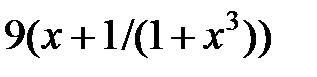
| |
| 2.5.14 | 1.815 | 0.3 | 1.2 | 5.6 | 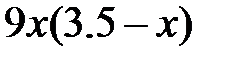
| |||
| 2.5.15 | 1.5 | 0.875 | 0.5 | 1.8 | 5.6 | 8.5 | 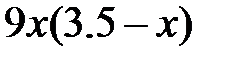
| |
| 2.5.16 | 1.8 | 1.215 | 0.4 | 1.2 | 3.2 | 8.5 | 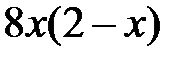
| |
| 2.5.17 | 1.215 | 0.4 | 1.5 | 3.2 | 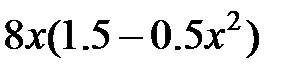
| |||
| 2.5.18 | 2.3 | 1.725 | 0.5 | 1.2 | 3.5 | 8.2 | 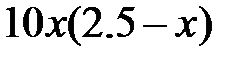
| |
| 2.5.19 | 2.5 | 1.725 | 0.5 | 1.5 | 3.5 | 12.08 | 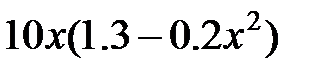
| |
| 2.5.20 | 2.8 | 1.725 | 1.5 | 0.4 | 8.3 | 3.5 | 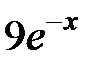
| |
| 2.5.21 | 3.0 | 2.015 | 1.5 | 0.5 | 8.3 | 2.8 | 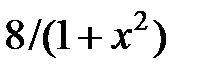
| |
| 2.5.22 | 1.5 | 0.925 | 1.2 | 0.4 | 8.3 | 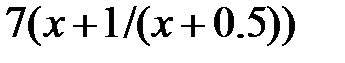
| ||
| 2.5.23 | 1.7 | 0.925 | 1.2 | 0.5 | 7.5 | 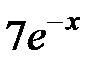
| ||
| 2.5.24 | 2.0 | 1.215 | 1.8 | 0.4 | 7.0 | 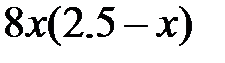
| ||
| 2.5.25 | 2.2 | 1.215 | 1.8 | 0.5 | 6.5 | 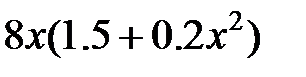
| ||
| 2.5.26 | 2.5 | 1.515 | 0.3 | 1.8 | 3.5 | 8.3 | 
| |
| 2.5.27 | 3.0 | 1.875 | 1.5 | 0.6 | 8.3 | 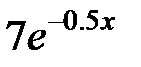
| ||
| 2.5.28 | 1.5 | 0.875 | 0.5 | 1.8 | 5.6 | 8.5 | 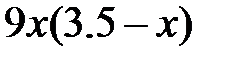
| |
| 2.5.29 | 1.215 | 0.4 | 1.5 | 3.2 | 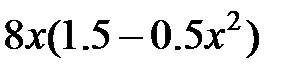
| |||
| 2.5.30 | 2.3 | 1.725 | 0.5 | 1.2 | 3.5 | 8.2 | 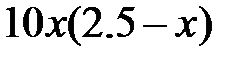
|
Таблица к задаче 2.6
В задаче 2.6 взять входные данные k(x), f(x), ua, ub из задачи 2.1, 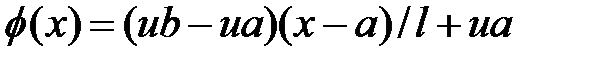 ,
, 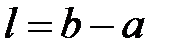 .
.
ПРИЛОЖЕНИЕ 2.B
 Для нахождения решения стационарного уравнения теплопроводности
Для нахождения решения стационарного уравнения теплопроводности  дважды проинтегрируем его. Первое интегрирование дает такой результат
дважды проинтегрируем его. Первое интегрирование дает такой результат
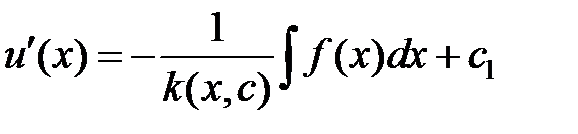 .
.
Проинтегрируем полученное соотношение еще раз получим:
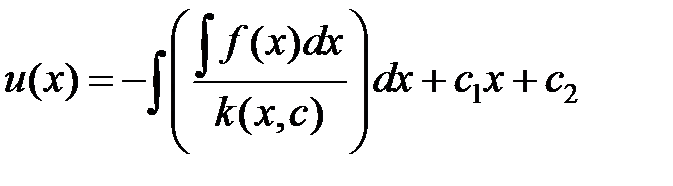 .
.
Константы 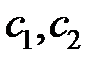 находятся из граничных условий:
находятся из граничных условий:
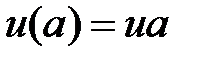 ,
, 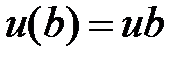 .
.
Пример решения задачи 2.1. Пусть 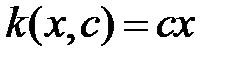 .
.
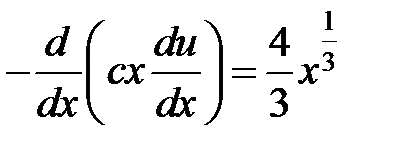 ,
,
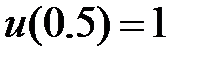 ,
, 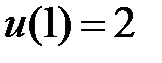 .
.
Проинтегрируем уравнение: 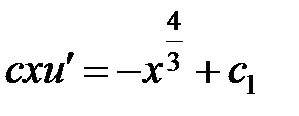 . Повторное интегрирование дает соотношение:
. Повторное интегрирование дает соотношение: 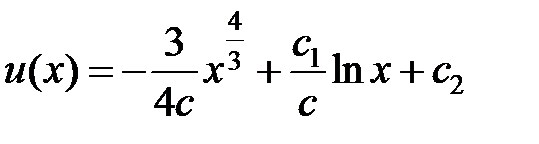 .
.
Найдем константы 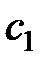 и
и 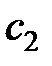 , при условии, что
, при условии, что 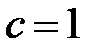 :
: 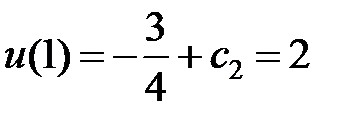 ;
; 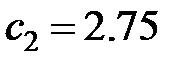
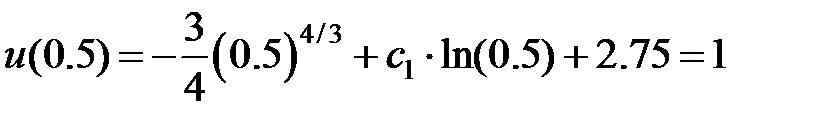 , поэтому
, поэтому  .
.
Окончательно, решение примет вид: 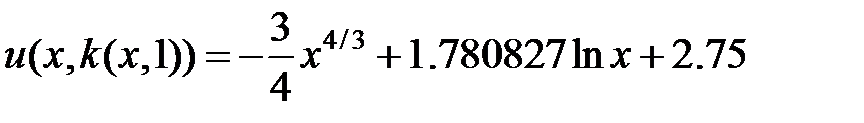 .
.
Для проверки можно подставить найденное решение в исходное уравнение и проверить выполнение граничных условий.
|
|
