Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

ЛР 1. 2. Численное решение стационарных и нестационарных задач теплопроводности

Отчет по ИПР должен содержать следующие материалы по каждой задаче:

1) постановка задачи;

2) необходимый теоретический материал;

3) тестовый пример и результаты вычислительного эксперимента по тесту (если необходимо);

4) полученные результаты и их анализ;

5) графический материал (если необходимо);

6) тексты программ.

Варианты заданий к заданиям 2.1-2.6 даны в ПРИЛОЖЕНИИ 2.A.

Фрагмент решения задачи 2.1 дан в ПРИЛОЖЕНИИ 2.B.

Задание 2.1. Промоделировать стационарные процессы теплопроводности стержня в зависимости от входных данныхзадачи:

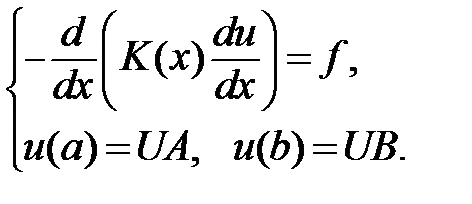
ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ:

1. Представить коэффициент теплопроводности K(x) в виде функции двух переменных x и с: K(x)=K(x, c), где с - параметр.

2. При заданных в индивидуальном варианте функциях K(x) ( чтосоответствует K(x, 1 )), f(x) и значениях UA, UB найти аналитическое решение задачи символьно (см. ПРИЛОЖЕНИЯ 2.B и 2.С).

3. Изменяя значения параметра с в коэффициенте теплопроводности, найти решения задачи для наборов параметров 1-3 (см. таблицу ниже).

4. На одном чертеже построить графики найденных решений. Cравнить полученные результаты.

5. Аналогично п.2, найти аналитическое решение для набора параметров 4. На одном чертеже построить графики решений для наборов 1 и 4. Cравнить полученные результаты.

6. Изменяя граничные условия UA, UB, построить решения для наборов параметров 5-7.

Таблица наборов параметров

Задание 2.2. Найти приближенное решение краевой задачи методом конечных разностей:

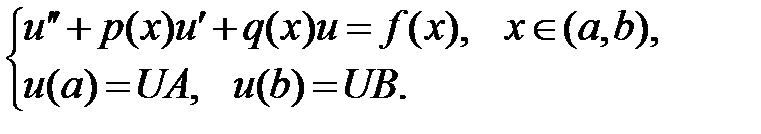
c заданной точностью и построить его график.

ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ:

1. Cоставить разностную схему второго порядка точности и выписать коэффициенты матрицы системы уравнений и коэффициенты правой части.

2. Подготовить тестовый пример и провести расчет для него. Построить на одном чертеже графики приближенного и точного решений для тестового примера. После проверки правильности работы программы перейти к решению основной задачи.

3. Для отыскания решения задачи с заданной точностью произвести расчет с начальным шагом h, затем уменьшить шаг вдвое. Вывести на экран два соседних приближенных решения и сравнить результаты. Если заданная точность не достигнута, то продолжить уменьшение шага.

4. Построить график найденного решения и указать шаг, при котором заданная точность достигается.

Задание 2.3. Методом конечных разностей найти приближенное решение указанной в индивидуальном варианте краевой задачи c точностью и построить его график. Решение системы разностных уравнений найти, используя метод прогонки.