Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Классический метод расчета переходных процессов
|
|
Расчет переходных процессов классическим методом основан на непосредственном решении описывающих их дифференциальных уравнений. Выражение для свободной составляющей определяется количеством и видом корней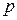 
характеристического уравнения. Характеристическое уравнение 
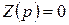можно получить, приравняв нулю входное сопротивление 
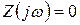и заменив 
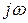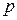на в выражении для входного сопротивления, определенного относительно любой ветви схемы. Рекомендуется определять входное сопротивление относительно ветви с реактивным элементом.
В общем случае, когда корни характеристического уравнения вещественные и не равны между собой, выражение для свободной составляющей имеет вид
.
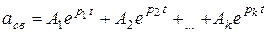Если корни характеристического уравнения вещественны и равные, то
.
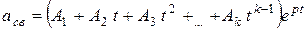В случае комплексно-сопряженных корней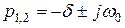 
свободная составляющая
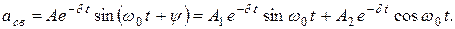
Рекомендуется следующий порядок расчета
1. Рассчитывают установившийся режим до и после коммутации.
2. С помощью уравнени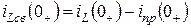й
и 
находят свободные составляющие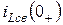 
и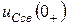 
независимых начальных услови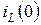й 
и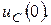 
3. Составляют характеристическое уравнение и находят его корни.
4. В зависимости от вида корней записывают выражения для искомых переходных токов и напряжений в общем виде, в которых неизвестными являются постоянные интегрирования. Существуют два способа определения постоянных интегрирования.
5. После определения постоянных интегрирования, записывают окончательно выражения для токов и напряжений переходного режима
.
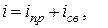
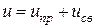Расчет переходных процессов в цепях первого порядка
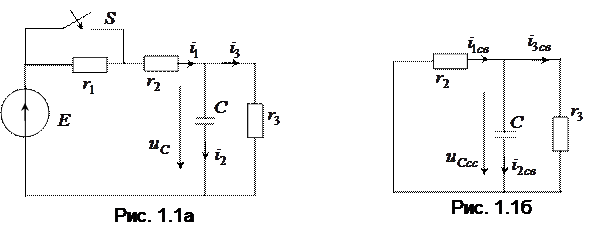
1. В схеме (рис. 1.1а)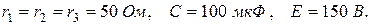 
Найти выражения для токов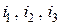 
и напряжения 
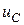переходного процесса.
Пример решения
До коммутации в схеме был установившийся режим постоянного тока
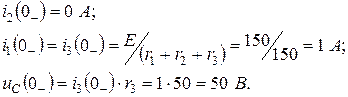
Напряжение на конденсаторе в момент коммутации не изменяется, следовательно,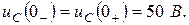 
Принужденный режим послекоммутационной схемы обусловлен воздействием постоянной ЭДС. Поэтому, начиная с момента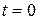 
, принужденные составляющие токов и напряжений остаются постоянными:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
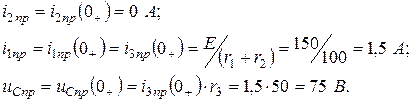
Составляем характеристическое уравнение и находим его корни
Определяем комплекс входного сопротивления послекоммутационной схемы относительно ветви с конденсатором (рис. 1.1б):
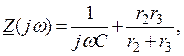
тогда характеристическое уравнение
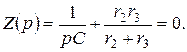
Корень характеристического уравнения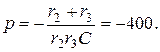 
Записываем в общем виде выражения для токов и напряжения на конденсаторе в переходном режиме для послекоммутационной схемы:
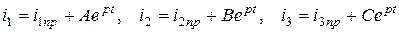и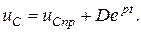 
Постоянные интегрирования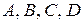 
можно определить двумя способами.
Первый способ
Составляем систему уравнений по законам Кирхгофа для принужденного режима и решаем ее при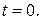 
,
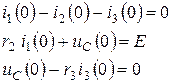откуда
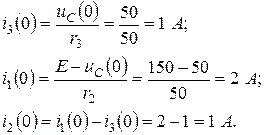
Определяем постоянные интегрирования при :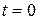
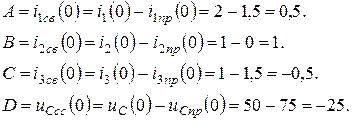
Второй способ
Составляем систему уравнений по законам Кирхгофа для свободного режима при 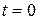(рис, 1.1б), когда исключен источник принужденного режима.
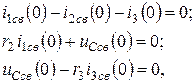
откуда
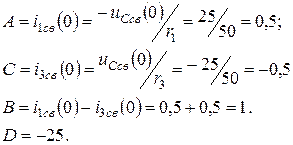
Подставив постоянные интегрирования в выражения токов и напряжения на конденсаторе в общем виде для переходного режима, получим
|
|
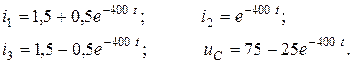
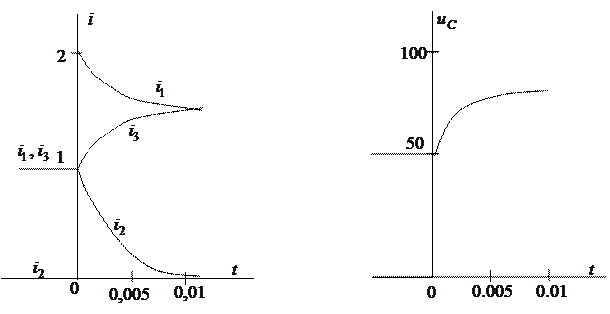