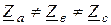Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вид нагрузки фаз
|
|
Контрольная работа
ДЛЯ СТУДЕНТОВ ЗАОЧНОГО ОТДЕЛЕНИЯ
по курсу ТОЭ (2 ЧАСТЬ)
Задания и методические указания Контрольная работа по ТОЭ
Задача 1. Трехфазные цепи
Вариант определяется последней цифрой зачетной книжки и соответствует столбцу таблицы 2.1.
К симметричной четырехпроводной системе питания с линейным напряжением, частотой 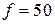 Гц подключить несимметричный трехфазный потребитель, фазные сопротивления которого заданы вариантом..
Гц подключить несимметричный трехфазный потребитель, фазные сопротивления которого заданы вариантом..
1) Изобразить схему электрической цепи.
2) Рассчитать комплексное сопротивление фазы, содержащей катушку индуктивности, коэффициент мощности данной фазы.
4) Определить величину компенсирующей емкости, при которой 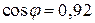 для фазы, содержащей катушку индуктивности.
для фазы, содержащей катушку индуктивности.
5) Изобразить схему четырехпроводной трехфазной цепи с учетом найденных компенсирующих емкостей и рассчитать
– фазные напряжения и токи потребителя;
– ток в нулевом проводе;
– построить векторные диаграммы напряжений и токов;
– рассчитать соотношение между линейными и фазными напряжениями.
Примечание: п.5) может выполняться методом компьютерного моделирования.
6) Методом компьютерного моделирования провести анализ электрического состояния трехпроводной трехфазной цепи (п. 5): определить напряжение смещения нейтрали, фазные напряжения и токи потребителя
– в номинальном режиме: схема с учетом найденной экспериментально компенсирующей емкости;
– при обрыве линии провода;
– при коротком замыкании одной фазы
7)По данным исследования построить векторные диаграммы напряжений и токов для всех режимов.
Вид нагрузки фаз
Таблица 1.2
| № столбцов | ||||||||||
| ||||||||||
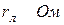
| ||||||||||
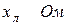
| ||||||||||
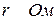
| ||||||||||
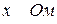
|
Краткая теория
При изучении темы следует понимать ее значимость: почти все электроснабжение, включающее производство, передачу и распределение электрической энергии осуществляется с помощью трехфазных цепей, которые представляют собой своеобразную систему передачи энергии, где от каждого " генератора" ЭДС энергия передается одним проводом. Таким образом, для передачи той же мощности экономия на проводах почти в два раза. Необходимо хорошо усвоить все определения трехфазной цепи: фазные и линейные токи, напряжения, симметричной и несимметричной цепи.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Важным свойством трехфазной цепи является то, что независимо от характера нагрузки сумма линейных напряжений всегда равна нулю.
Способ соединения трехфазной нагрузки не зависит от способа соединения фаз генератора. Возможность переключения фаз со звезды на треугольник, и наоборот, часто используется для регулирования тока и мощности.
При анализе трехфазных цепей можно пользоваться всеми методами расчета цепей синусоидального тока. При расчете симметричных цепей удобно использовать некоторые специфические приемы, т.е. расчет вести только для одной из фаз, для получения токов и напряжений в двух других фазах достаточно воспользоваться операторами а и 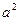 . (а = -
. (а = - 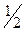 + j
+ j 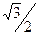 ), (
), (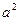 == -
== - 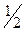 - j
- j 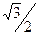 ).
).
Необходимо понимать, что нейтральный провод обеспечивает сохранение симметрии фаз. Для несимметричных цепей ток в нейтральном проводе не равен нулю.
Важно знать, что преимуществом четырехпроводной цепи является то, что при изменении режима работы одной из фаз режимы других фаз не изменяются. Это свойство получило название независимость работы фаз, и крайне важно при несимметричной нагрузке. На практике нейтральный провод выбирают меньшего сечения.
Следует помнить, что: к трехфазным потребителям электрической энергии относятся трехфазные синхронные и асинхронные двигатели и трансформаторы (с нагрузкой), электрические печи, приборы электрического освещения и др. Большинство потребителей носит активно индуктивный характер.
Следует понимать, что в цепях синусоидального тока полезной является активная мощность. Существуют различные способы ее увеличения, в том числе за счет уменьшения реактивной мощности. Одним из таких способов является использование компенсаторов реактивной мощности, которые имеют емкостной характер и дополнительно включаются в цепь с индуктивной нагрузкой. Общее реактивное сопротивление уменьшается, а значит, уменьшается и реактивная мощность.
Методы расчета трехфазной цепи
Трехфазная цепь представляет собой сочетание трех однофазных цепей. Для ее расчета могут быть применены все известные методы расчета однофазных цепей.
При расчете трехфазных цепей рекомендуется использовать принятую систему обозначений: токи, ЭДС, напряжения, сопротивления источника следует обозначать соответствующей буквой с фазным индексом в виде прописной буквы: 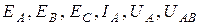 и т.д.; токи, напряжения, сопротивления приемника – соответственно с фазным индексом в виде строчной буквы:
и т.д.; токи, напряжения, сопротивления приемника – соответственно с фазным индексом в виде строчной буквы:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
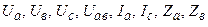 и т.д.
и т.д.
Во всех рассматриваемых вариантах расчета источник принимается симметричным.
 Если входное напряжение задается линейными значениями, а в расчете предлагается использовать фазные значения напряжения, то при переходе отлинейных значений к фазным (и наоборот) необходимо учитывать смещение векторов линейного и фазного напря-жений (рис. 3.2):
Если входное напряжение задается линейными значениями, а в расчете предлагается использовать фазные значения напряжения, то при переходе отлинейных значений к фазным (и наоборот) необходимо учитывать смещение векторов линейного и фазного напря-жений (рис. 3.2):
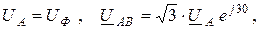
Рассмотрим варианты расчета трехфазных цепей. При выполнении расчетно-графической работы студен-там предлагается для расчета заданной схемы применить наиболее рацио-нальный метод или сочетание методов и приемов, требующих минимального объема расчетной работы.
1. Расчет несимметричной трехфазной цепи при соединении по схеме «звезда – звезда» (рис.3.3):
|
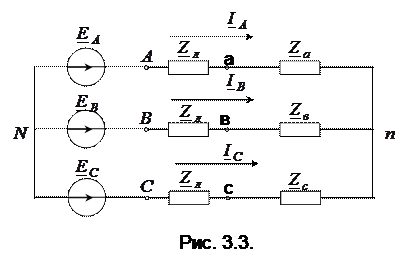
Расчет такой цепи можно выполнить, например, методом узловых потенциалов. Принимая потенциал точки  равным нулю, определим потенциал точки
равным нулю, определим потенциал точки 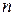 :
:
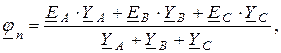
где
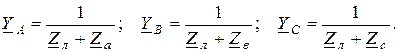
Тогда по закону Ома определим токи в фазах:

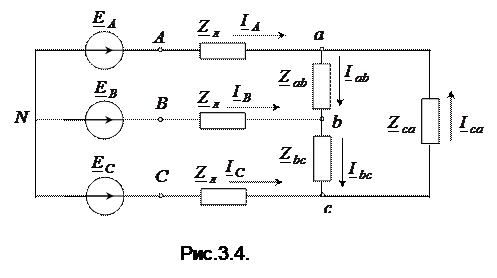 2. Расчет несимметричной трехфазной цепи при соединении приемника по схеме треугольник (рис. 3.4).
2. Расчет несимметричной трехфазной цепи при соединении приемника по схеме треугольник (рис. 3.4).
В такой цепи линейные токи можно определить, используя известные методы расчета (метод узловых потенциалов), предварительно преобразовав нагрузку в эквивалентное соединение звездой (рис. 3.3). Фазные токи в исходной схеме (рис. 3.4) определяются по выражениям
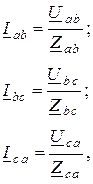
где
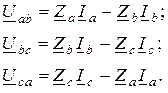
Задача 2. Переходные процессы в линейных электрических цепях
с сосредоточенными параметрами.
Найти выражения для токов и напряжений в ветвях в заданной согласно варианту схеме классическим методом.
Вариант контрольной работы состоит из двух цифр разделенной точкой.
Первая цифра варианта задает по таблице 2.1 расчетную схему.
Вторая цифра – столбец таблицы 2.2.
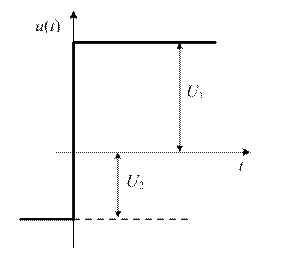
Форма входного напряжения определяется четностью варианта: четный – форма на рис. 2.1; нечетный – форма на рис. 2.2.
Для этого необходимо:
1) Рассчитать установившейся режим до коммутации. Найти значения токов и напряжений при U = U 1.
2) Рассчитать установившейся режим после коммутации. Найти значения токов и напряжений при U = U 2.
3) Найти свободные составляющие 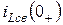 или
или 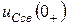 независимых начальных условий
независимых начальных условий 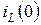 и
и 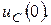
4) Составить характеристическое уравнение и найти его корни. Записать выражения для искомых переходных токов и напряжений в общем виде, в которых неизвестными являются постоянные интегрирования.
5) Найти постоянные интегрирования и записать выражения для токов и напряжений переходного режима.
6) Построить графики переходных токов и напряжений в программе Mathcad.
7) Получить компьютерную модель заданной схемы в программе Multisim. С помощью виртуального осциллографа получить зависимости напряжения на временной плоскости. Сравнить с графиками из п. 6.
Входное напряжение:
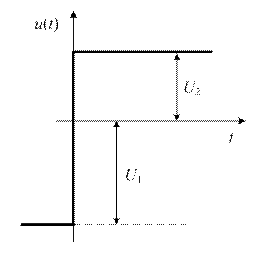
| 
|
| Рис. 2.1 | Рис. 2.2 |
Таблица 2.1
| № | Расчетная схема |
| 1. 7. 13. 19. | 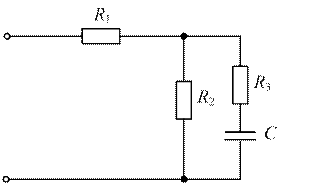
|
| 2. 8. 14. 20. | 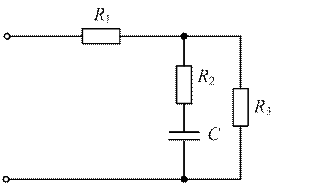
|
| 3. 9. 15. | 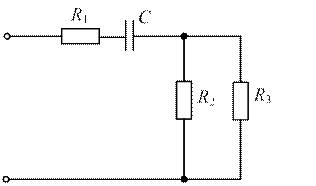
|
| 4. 10. 16. | 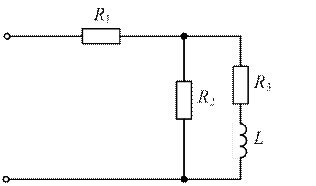
|
| 5. 11. 17. | 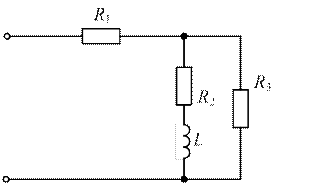
|
| 6. 12. 18. | 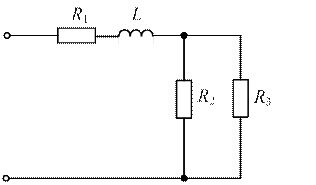
|
Таблица 2.2
| № | ||||||||||
| R 1, Ом | ||||||||||
| R 2, Ом | ||||||||||
| R 3, Ом | ||||||||||
| L, Гн | 0, 4 | 0, 2 | 0, 6 | 0, 1 | 0, 5 | 0, 8 | 0, 3 | 0, 45 | 0, 7 | 0, 9 |
| C, мкФ | ||||||||||
| U 1, В | ||||||||||
| U 2, В |
Краткая теория и примеры
Переходные процессы возникают при коммутации электрической цепи или при изменении параметров элементов схемы. Во время переходного процесса один установившийся режим сменяется другим. Второй установившийся режим называется принужденным. Принято, что коммутация происходит мгновенно в момент 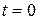 . Установившийся режим до коммутации заканчивается при
. Установившийся режим до коммутации заканчивается при 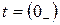 . При
. При 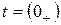 начинается переходный процесс, а принужденный режим устанавливается при
начинается переходный процесс, а принужденный режим устанавливается при 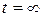 .
.
По законам коммутации в момент 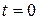 не могут изменяться скачком напряжения
не могут изменяться скачком напряжения 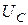 на емкостных элементах или суммарный заряд
на емкостных элементах или суммарный заряд 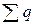 на обкладках конденсаторов, присоединенных к любому узлу схемы после коммутации, а также токи
на обкладках конденсаторов, присоединенных к любому узлу схемы после коммутации, а также токи 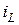 в ветвях с индуктивными элементами или суммарное потокосцепление
в ветвях с индуктивными элементами или суммарное потокосцепление  каждого контура послекоммутационной схемы. Остальные токи и напряжения в момент коммутации могут изменяться скачком.
каждого контура послекоммутационной схемы. Остальные токи и напряжения в момент коммутации могут изменяться скачком.
При действии в цепи постоянных, синусоидальных и других периодических напряжений и токов переходные процессы рассчитываются классическим или операторным методами.
Во время переходного процесса токи и напряжения представляются в виде суммы принужденного и свободного составляющих, которые рассчитываются отдельно: 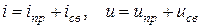 .
.
Установившиеся до коммутации и принужденные составляющие определяются известными методами расчета цепей постоянного или переменного токов. Свободные составляющие обусловлены изменением энергии реактивных элементов схемы и затухают до нуля к окончанию переходного процесса.
При действии в цепи непериодических источников тока или напряжения расчет целесообразно вести методом наложения с использованием интеграла Дюамеля.
Расчет переходных процессов в сложных электрических цепях с большим количеством реактивных элементов и в нелинейных электрических цепях ведут численным методом.
|
|