
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оценка генеральной доли
|
|
Пусть требуется оценить долю тех объектов заданной генеральной совокупности, которые удовлетворяют некоторому условию 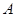 – генеральную долю
– генеральную долю 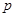 . Для этого из генеральной совокупности выделяют выборку, и по результатам её обследования находят долю тех объектов, которые удовлетворяют условию
. Для этого из генеральной совокупности выделяют выборку, и по результатам её обследования находят долю тех объектов, которые удовлетворяют условию 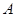 – выборочную долю
– выборочную долю 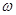 . Очевидно, что
. Очевидно, что 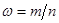 , где
, где 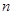 – объем выборки,
– объем выборки, 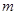 – число тех её объектов, которые удовлетворяют условию
– число тех её объектов, которые удовлетворяют условию 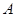 . Выборочная доля в данном случае является той величиной, с помощью которой мы получим информацию о неизвестном значении генеральной доли.
. Выборочная доля в данном случае является той величиной, с помощью которой мы получим информацию о неизвестном значении генеральной доли.
Таким образом, выборочная доля 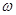 является оценкой генеральной доли
является оценкой генеральной доли 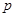 .
.
Пример. 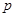 – доля бракованных деталей генеральной совокупности,
– доля бракованных деталей генеральной совокупности, 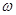 – доля бракованных деталей в выборке. Условие (событие)
– доля бракованных деталей в выборке. Условие (событие) 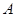 – деталь, взятая наудачу из генеральной совокупности – бракована.
– деталь, взятая наудачу из генеральной совокупности – бракована.
Простейший способ оценивания – точечное оценивание – подразумевает использование приближенного равенства 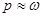 .
.
Как и всякая оценка, выборочная доля 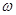 является случайной величиной. Действительно, выборка из генеральной совокупности выделяется случайным образом. Соответственно то значение, которое примет выборочная доля, будет случайным.
является случайной величиной. Действительно, выборка из генеральной совокупности выделяется случайным образом. Соответственно то значение, которое примет выборочная доля, будет случайным.
Следующие теоремы характеризуют выборочную долю как случайную величину.
Теорема 1. Математическое ожидание выборочной доли равно генеральной доле:
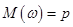 .
.
Среднее квадратическое отклонение 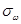 (
(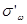 ) выборочной доли вычисляется по формулам
) выборочной доли вычисляется по формулам
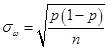
– в случае повторной выборки и
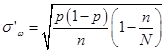
– в случае бесповторной выборки, где 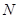 – объем генеральной совокупности.
– объем генеральной совокупности.
Напомним, что по определению среднего квадратического отклонения в случае повторной выборки имеем 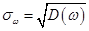 (аналогично в случае бесповторной выборки).
(аналогично в случае бесповторной выборки).
Замечание. При применении формул Теоремы 1 полагают
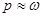 .
.
Теорема 2. Закон распределения выборочной доли неограниченно приближается к нормальному закону при неограниченном увеличении объема выборки.
Подобно тому, как мы это сделали в предыдущем параграфе, как следствие Теоремы 2, получаем формулу доверительной вероятности:
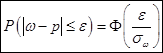
– в случае повторной выборки. Заменяя в последнем равенстве 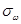 на
на 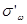 , получаем формулу доверительной вероятности в случае бесповторной выборки.
, получаем формулу доверительной вероятности в случае бесповторной выборки.
По определению, величина 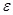 , фигурирующая в формуле доверительной вероятности, называется предельной ошибкой выборки. Интервал
, фигурирующая в формуле доверительной вероятности, называется предельной ошибкой выборки. Интервал 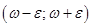 называется доверительным интервалом.
называется доверительным интервалом.
Выше было указано, в чем состоит точечная оценка генеральной доли. Интервальное оценивание сводится, например, к вычислению значения доверительной вероятности при заданной предельной ошибке выборки.
Теорема 3. В случае повторной выборки выборочная доля является несмещенной и состоятельной оценкой генеральной доли.
Пример. Выборочные данные о надое молока для 100 коров из 1000 представлены таблицей:
| Надой молока, ц | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 
|
| Число коров |
1. Найти вероятность того, что доля всех коров с надоем молока более 40 ц отличается от такой доли в выборке не более чем на 0, 05 (по абсолютной величине), для случая повторной и бесповторной выборок.
2. Найти границы, в которых с вероятностью 0, 9596 заключена доля всех коров с надоем более 40 ц.
3. Сколько коров надо обследовать, чтобы с вероятностью 0, 9786 для генеральной доли коров с надоем более 40 ц можно было гарантировать те же границы что и в п.2.
Решение. Число 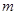 коров с надоем более 40 ц равно 34 (
коров с надоем более 40 ц равно 34 (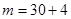 , см. заданный вариационный ряд). Тогда
, см. заданный вариационный ряд). Тогда 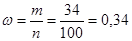 .
.
Для нахождения доверительной вероятности п. 1 задания воспользуемся одноименной формулой при 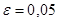 .
.
Пусть рассматриваемая выборка – повторная. Тогда по формуле Теоремы 1, учитывая Замечание, получаем
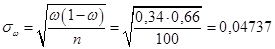 .
.
Следовательно
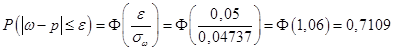 .
.
Аналогично, в случае бесповторной выборки:
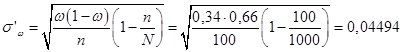 ,
,
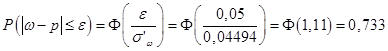 .
.
Доверительным в данном случае является интервал 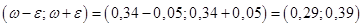 . Таким образом, неизвестное значение доли всех коров с надоем более 40 ц накрывается доверительным интервалом (0, 29; 0, 39) с вероятностью 0, 7109 в случае повторной выборки и с вероятностью 0, 733 в случае бесповторной выборки.
. Таким образом, неизвестное значение доли всех коров с надоем более 40 ц накрывается доверительным интервалом (0, 29; 0, 39) с вероятностью 0, 7109 в случае повторной выборки и с вероятностью 0, 733 в случае бесповторной выборки.
В п. 2 задания при заданном значении доверительной вероятности искомым является доверительный интервал. Поскольку значение выборочной доли известно, остается найти предельную ошибку выборки 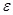 .
.
Пусть выборка – повторная. По условию, принимая во внимание формулу доверительной вероятности, имеем
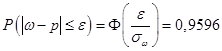 .
.
По таблице значений функции Лапласа найдем такое 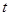 , что
, что 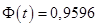 :
: 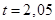 . Тогда
. Тогда 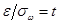 и, используя найденное выше значение
и, используя найденное выше значение 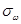 , получаем
, получаем
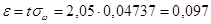 .
.
Соответственно, доверительным будет интервал:
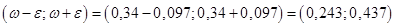 .
.
Пусть выборка – бесповторная. Аналогично предыдущему, получаем предельную ошибку выборки
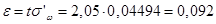
и доверительный интервал:
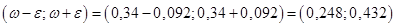 .
.
Таким образом, доля всех коров с надоем молока более 40 ц с вероятностью 0, 9596 накрывается доверительным интервалом (0, 243; 0, 437) в случае повторной выборки и интервалом (0, 248; 0, 432) в случае бесповторной выборки.
В п. 3 по заданным значениям доверительной вероятности и предельной ошибки выборки найдем необходимый объем выборки. Из начла решения заимствуем значение выборочной доли 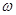 , найденное по исходному вариационному ряду.
, найденное по исходному вариационному ряду.
Пусть выборка – повторная. По условию, принимая во внимание формулу доверительной вероятности, имеем:
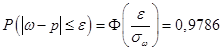 .
.
По таблице значений функции Лапласа найдем такое 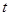 , что
, что 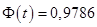 :
: 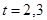 . Тогда
. Тогда 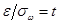 и,
и, 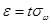 . Подставляя вместо
. Подставляя вместо 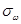 выражение из Теоремы 1, приходим к уравнению относительно неизвестной величины
выражение из Теоремы 1, приходим к уравнению относительно неизвестной величины 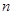 :
:
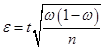 .
.
Решая это уравнение относительно 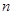 , подставляя в полученную формулу известные величины, завершаем решение
, подставляя в полученную формулу известные величины, завершаем решение
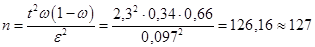
(заметим, что, как и ранее, округление здесь произведено в большую сторону).
Аналогично, в случае бесповторной выборки из условия и формулы доверительной вероятности следует равенство
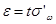
или, принимая во внимание известное выражение для 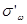 (см. Теорему 1):
(см. Теорему 1):
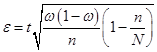 .
.
Решая это уравнение относительно 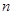 , получаем
, получаем
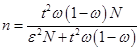 .
.
Подставляя в правую часть последнего равенства известные значения, окончательно имеем:
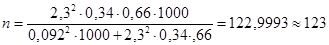 .
.
Таким образом, в повторную выборку надо взять 127 коров, чтобы с вероятностью 0, 9786 можно было утверждать, что доля всех коров с надоем молока более 40 ц накрывается доверительным интервалом (0, 243; 0, 437). Аналогично, в бесповторную выборку надо взять 123 коровы, чтобы с вероятностью 0, 9786 можно было утверждать, что доля всех коров с надоем молока более 40 ц накрывается доверительным интервалом (0, 248; 0, 432).
Домашнее задание: 9.19, 9.21, 9.23, 9.30.
|
|