Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Общий алгоритм Брезенхема.

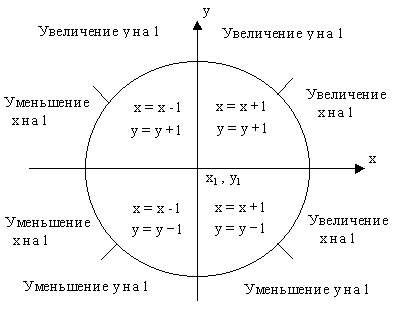
Чтобы реализация алгоритма Брезенхема была полной необходимо обрабатывать отрезки во всех октантах. Модификацию легко сделатть, учитывая в алгоритме номер квадранта, в котором лежит отрезок и его угловой коэффициепт. Когда абсолютная величина углового коэффициента больше 1, у постоянно изменяется на единицу, а критерий ошибки Брезенхема используется для принятия решения об изменении величины x. Выбор постоянно изменяющейся (на +1 или -1) кооординаты зависит от квадранта (рис.4.1.). Общий алгоритм может быть оформлен в следующем виде:

Обобщенный целочисленный алгоритм Брезенхема квадрантов

предполагается, что концы отрезка (x1, y1) и (x2, y2) не совпадают

все переменные считаются целыми

Sign - функция, возвращающая -1, 0, 1 для отрицательного, нулевого и положительного аргумента соответственно

инициализация переменных

x = x1

y = y1

 x = abs(x2 - x1)

 y = abs(y2 - y1)

s1 = Sign (x2 - x1)

s2 = Sign (y2 - y1)

обмен значений  x и  y в зависимости от углового коэффициента наклона отрезка

if  y <  x then

Врем =  x

 x =  y

 y = Врем

Обмен = 1

Else

Обмен = 0

End if

инициализация  с поправкой на половину пиксела

 = 2* y -  x

основной цикл

for i = 1 to  x

Plot (x, y)

while ( => 0)

if Обмен = 1 then

x = x + s1

Else

y = y + s2

End if

 =  - 2* x

End while

if Обмен = 1 then

y = y + s2

Else

x = x + s1

End if

 =  + 2* y

Next i

Finish

Рис.4.1. Разбор случаев для обобщенного алгоритма Брезенхема.

Пример 4.1. обобщенный алгоритм Брезенхема.

Для иллюсрации рассмотрим отрезок из точки (0, 0) в точку (-8, -4).

начальные установки

x = 0

y = 0

 x = 8

 y = 4

s1 = -1

s2 = -1

Обмен = 0

е = 0

результаты работы пошагового цикла

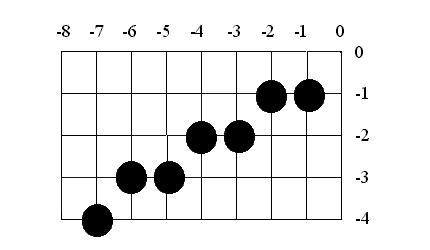
Рис.4.2. Результат работы обобщенного алгоритма Брезенхема в третьем квадранте.

На рис.4.2 продемонстрирован результат. Сравнение с рис. 2.2 показывает, что результаты работы двух алгоритмов отличаются.

В следующем разделе рассматривается алгоритм Брезенхема для генерации окружности.