
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
Состав сложного суждения
|
|
NB: Субъект и предикат в теоретической логике называют терминами суждения.
— связка устанавливает отношения между субъектом и предикатом суждения.
Обычно связка выражается словами " есть" или " не есть".
12) Простые суждения — суждения, составными частями которых являются понятия. Простое суждение можно разложить только на понятия.
Сложные суждения — суждения, составными частями которых являются простые суждения или их сочетания. Сложное суждение может рассматриваться как образование из нескольких исходных суждений, соединенных в рамках данного сложного суждения логическими союзами (связками). От того, при помощи какого союза связываются простые суждения, зависит логическая особенность сложного суждения.
Состав простого суждения
Простое (атрибутивное) суждение — это суждение о принадлежности предметам свойств (атрибутов), а также суждения об отсутствии у предметов каких-либо свойств. В атрибутивном суждении могут быть выделены термины суждения — субъект, предикат, связка, квантор.
·Субъект суждения — это мысль о каком-то предмете, понятие о предмете суждения (логическое подлежащее).
·Предикат суждения — мысль об известной части содержания предмета, которое рассматривается в суждении (логическое сказуемое).
·Логическая связка — мысль об отношении между предметом и выделенной частью его содержания (иногда только подразумевается).
·Квантор — указывает, относится ли суждение ко всему объёму понятия, выражающего субъект, или только к его части: «некоторые», «все» и т. п.
Состав сложного суждения
Сложные суждения состоят из ряда простых («Человек не стремится к тому, во что не верит, и любой энтузиазм, не подкрепляясь реальными достижениями, постепенно угасает»), каждое из которых в математической логике обозначается латинскими буквами (A, B, C, D… a, b, c, d…). В зависимости от способа образования различают конъюнктивные, дизъюнктивные, импликационные, эквивалентные и отрицательные суждения.
Дизъюнктивные суждения образуются с помощью разделительных (дизъюнктивных) логических связок (аналогичных союзу «или»). Подобно простым разделительным суждениям, они бывают:
· нестрогими (нестрогая дизъюнкция), члены которой допускают совместное сосуществование («то ли…, то ли…»). Записывается как 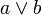 ;
;
· строгими (строгая дизъюнкция), члены которой исключают друг друга (либо одно, либо другое). Записывается как 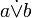 .
.
Импликационные суждения образуются с помощью импликации, (эквивалентно союзу «если …, то»). Записывается как 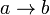 или
или 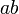 . В естественном языке союз «если …, то» иногда является синонимом союза «а» («Погода изменилась и, если вчера было пасмурно, то сегодня не одной тучи») и, в таком случае, означает конъюнкцию.
. В естественном языке союз «если …, то» иногда является синонимом союза «а» («Погода изменилась и, если вчера было пасмурно, то сегодня не одной тучи») и, в таком случае, означает конъюнкцию.
Конъюнктивные суждения образуются с помощью логических связок сочетания или конъюнкции (эквивалентно запятой или союзам «и», «а», «но», «да», «хотя», «который», «зато» и другим). Записывается как 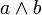 .
.
Эквивалентные суждения указывают на тождественность частей суждения друг другу (проводят между ними знак равенства). Помимо определений, поясняющих какой-либо термин, могут быть представлены суждениями, соединенными союзами «если только», «необходимо», «достаточно» (например: «Чтобы число делилось на 3, достаточно, чтобы сумма цифр, его составляющих, делилась на 3»). Записывается как 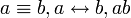 (у разных математиков по-разному, хотя математический знак тождества всё-таки
(у разных математиков по-разному, хотя математический знак тождества всё-таки  ).
).
Отрицательные суждения строятся с помощью связок отрицания «не». Записываются либо как a ~ b, либо как a b (при внутреннем отрицании типа «машина не роскошь»), а также с помощью черты над всем суждением при внешнем отрицании (опровержении): «не верно, что …» (a b).
13) Опираясь на уже известное определение простого суждения, категорическое суждение (суждение действительности) можно определить как такое, в котором что-то утверждается или отрицается относительно предмета мысли. Другими словами — это такое простое суждение, в котором между субъектом и предикатом устанавливается категорическая (утвердительная или отрицательная) связь, т.е. отношение тождества, подчинения, частичного совпадения, противоречия, противоположности и соподчинения: " Жучка есть собака», «Студент не есть профессор» и т.п.
Как и любое суждение, простое категорическое суждение может быть истинным («и») или ложным («л»). В языке это суждение выражается повествовательным предложением, при этом тесная связь и взаимозависимость суждения и предложения не является основанием для их отождествления.
Простые категорические суждения по количественному и качественному признакам подразделяются на виды. По количественному (объемному) показателю, выражаемому квантором, простые категорические суждения делятся на единичные, частные и общие.
Единичное суждение отражает единственный предмет мысли, т.е. субъект этого суждения — единичное понятие: «Крупнейший город Северо-Запада нашей страны расположен в устье Невы».
Частное суждение отражает некоторую совокупность предметов, но не всю, что и подчеркивается квантором: «Некоторые S есть Р», «Многие студенты — отличники», «Встречаются такие S, которые есть Р»
Общее суждение — суждение о всей без исключения предметной области, на которую направлено внимание, которая является предметом мысли. Это суждение с квантором " все" (ни один, каждый, всякий, без исключения и пр.) перед субъектом: «Все S есть Р», «Ни одно насекомое не есть млекопитающее», «Каждый школьник имеет дневник».
14) Так как простое категорическое суждение состоит из терминов S и Р, которые, являясь понятиями, могут рассматриваться со стороны объема, то любое отношение между S и Р в простых суждениях может быть изображено при помощи круговых схем Эйлера, отражающих отношения между понятиями. В суждениях термины S и Р могут быть либо распределены, либо не распределены. Термин считается распределенным” если его объем полностью включается в объем другого термина или полностью исключается из него. Термин будет нераспределенным, если его объем частично включается в объем другого термина или частично исключается из него. Проанализируем четыре вида суждений: А, I, Е, О (мы рассматриваем типичные случаи)[8].
Суждение А - общеутвердительное. Его структура: “Все S суть Р”.
15) есравнимыми среди простых суждений являются суждения, имеющие различные субъекты или предикаты.
Сравнимыми являются суждения с одинаковыми субъектами и предикатами.
Для иллюстрации отношений между простыми суждениями используется логический квадрат[2]:
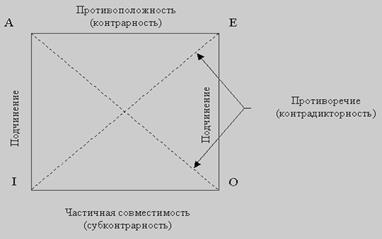
Рисунок 1. Логический квадрат
Среди сравнимых различают совместимые суждения, которые могут быть одновременно истинными, и несовместимые суждения, которые одновременно истинными быть не могут.
Совместимость бывает трех видов[3]: полная совместимость (эквивалентность); подчинение; частичная совместимость (субконтрарность).
Несовместимость бывает двух видов: противоположность (контрарность) и противоречивость (контрадикторность).
16) Непосредственные умозаключения - такие, в которых заключение выводится из одной посылки. Например, из суждения «Все адвокаты - юристы» можно получить новое суждение «Некоторые юристы - адвокаты». Непосредственные умозаключения дают нам возможность выявить знание о таких сторонах предметов, которое уже содержалось в исходном суждении, но не было явно выражено и явно осознано. В этих условиях мы делаем неявное - явным, неосознанное - осознанным.
К непосредственным умозаключениям относятся: превращение, обращение, противопоставление предикату, умозаключение по «логическому квадрату».
Превращение - такое умозаключение, в котором исходное суждение преобразуется в новое суждение, противоположное по качеству, и с предикатом, противоречащим предикату исходного суждения.
Чтобы превратить суждение, надо изменить его связку на противоположную, а предикат - на противоречащее понятие. Если посылка выражена не в явной форме, то надо преобразовать ее в соответствии со схемами суждений А, Е, I, О.
Если посылка записана в форме суждения «Не все S суть Р», то его надо преобразовать в частноотрицательное: «Некоторые S не суть Р».
Примеры и схемы превращения:
А:
Все студенты первого курса изучают логику.
Ни один студент первого курса не изучает не логику.
Схема:
Все S суть Р.
Ни одно S не суть не-Р.
Е: Ни одна кошка не является собакой.
Всякая кошка является не-собакой.
Ни один S не есть Р.
Все S есть не-Р.
I: Некоторые адвокаты суть спортсмены.
Некоторые адвокаты не суть не-спортсмены.
Некоторые S суть Р.
Некоторые S не суть не-Р.
О: Некоторые адвокаты не суть спортсмены.
Некоторые адвокаты суть не-спортсмены.
Некоторые S не суть Р.
Некоторые S суть не-Р.
Обращение - такое непосредственное умозаключение, в котором происходит перемена мест субъекта и предиката при сохранении качества суждения.
Обращение подчиняется правилу распределенности терминов: если термин не распределен в посылке, то он не должен быть не распределен и в заключении.
Если обращение ведет к изменению исходного суждения по количеству (из общего исходного получается новое частное суждение), то такое обращение называется обращением с ограничением; если обращение не ведет к изменению исходного суждения по количеству, то такое обращение является обращением без ограничения.
Примеры и схемы обращения:
А: Общеутвердительное суждение обращается в частноутвердительное.
Все адвокаты - юристы.
Некоторые юристы - адвокаты.
Все S суть Р.
Некоторые Р суть S.
Общеутвердительные выделяющие суждения обращаются без ограничения. Всякое правонарушение (и только правонарушение) суть противоправное деяние.
Всякое противоправное деяние суть правонарушение.
Схема:
Все S, и только S, суть Р.
Все Р суть S.
Е: Общеотрицательное суждение обращается в общеотрицательное (без ограничения).
Ни один адвокат не судья.
Ни один судья не адвокат.
Ни один S не есть Р.
Ни один Р не есть S.
I: Частноутвердительные суждения обращаются в частноутвердительные.
Некоторые юристы - спортсмены.
Некоторые спортсмены - юристы.
Некоторые S суть Р.
Некоторые Р суть S.
Частноутвердительные выделяющие суждения обращаются в общеутвердительные:
Некоторые юристы, и только юристы, являются адвокатами.
Все адвокаты суть юристы.
Некоторые S, и только S, суть Р.
Все Р суть S.
О: Частноотрицательные суждения не обращаются.
Логическая операция обращения суждения имеет большое практическое значение. Незнание правил обращения приводит к грубым логическим ошибкам. Так, довольно часто общеутвердительное суждение обращается без ограничения. Например, суждение «Все юристы должны знать логику» обращается в суждение «Все изучающие логику - юристы». Но это неверно. Верно суждение «Некоторые изучающие логику - юристы».
Противопоставление предикату - это последовательное применение операций превращения и обращения - преобразование суждения в новое суждение, в котором субъектом становится понятие, противоречащее предикату, а предикатом - субъект исходного суждения; меняется качество суждения.
Например, из суждения «Все адвокаты - юристы» можно, противопоставляя предикат, получить «Ни один не-юрист не является адвокатом». Схематически:
Все S суть Р.
Ни одно не- Р не есть S.
Умозаключение по «логическому квадрату». «Логический квадрат» - это схема, выражающая истинностные отношения между простыми суждениями, имеющими один и тот же субъект и предикат. В данном квадрате вершины символизируют известные нам по объединенной классификации простые категорические суждения: А, Е, О, I. Стороны и диагонали можно рассматривать как логические отношения между простыми суждениями (кроме эквивалентных). Так, верхняя сторона квадрата обозначает отношение между А и Е - отношение противоположности; нижняя сторона -отношение между О и I - отношение частичной совместимости. Левая сторона квадрата (отношение между А и I) и правая сторона квадрата (отношение между Е и О) - отношение подчинения. Диагонали обозначают отношения между А и О, Е и I, которые называются противоречием.
Отношение противоположности имеет место между суждениями общеутвердительными и общеотрицательными (А-Е). Сущность этого отношения состоит в том, что два противоположных суждения не могут быть одновременно истинными, но могут быть одновременно ложными. Поэтому если одно из противоположных суждений истинно, то другое непременно ложно, но если одно из них ложно, то о другом суждении еще нельзя безоговорочно утверждать, что оно истинно, - оно неопределенно, т. е. может оказаться как истинным, так и ложным. Например, если истинно суждение «Всякий адвокат является юристом», то противоположное ему суждение «Ни один адвокат не является юристом» будет ложно.
Но если ложно суждение «Все студенты нашего курса раньше изучали логику», то противоположное ему «Ни один студент нашего курса раньше не изучал логику» будет неопределенным, т. е. оно может оказаться как истинным, так и ложным.
Отношение частичной совместимости имеет место между суждениями частноутвердительными и частноотрицательными (I - О). Такие суждения не могут быть одновременно ложными (по крайней мере одно из них истинно), но могут быть одновременно истинными. Например, если ложно суждение «Иногда можно опаздывать на урок», то суждение «Иногда нельзя опаздывать на урок» будет истинным.
Но если одно из суждений истинно, то другое суждение, находящееся с ним в отношении частичной совместимости, будет неопределенным, т.е. оно может оказаться как истинным, так и ложным. Например, при истинности суждения «Некоторые люди изучают логику» суждение «Некоторые люди не изучают логику» будет истинным или ложным. Но при истинности суждения «Некоторые атомы делимы» суждение «Некоторые атомы не являются делимыми» будет ложным.
Отношение подчинения существует между общеутвердительными и частноутвердительными суждениями (А-I), а также между общеотрицательными и частноотрицательными суждениями (Е-О). При этом А и Е являются подчиняющими, а I и О -подчиненными суждениями.
Отношение подчинения состоит в том, что из истинности подчиняющего суждения обязательно следует истинность подчиненного суждения, но обратное необязательно: при истинности подчиненного суждения подчиняющее будет неопределенным - оно может оказаться как истинным, так и ложным.
Но если подчиненное суждение ложно, то подчиняющее будет тем более ложным. Обратное опять-таки необязательно: при ложности подчиняющего суждения подчиненное может оказаться как истинным, так и ложным.
Например, при истинности подчиняющего суждения «Все адвокаты - юристы» подчиненное суждение «Некоторые адвокаты - юристы» будет тем более истинным. Но при истинности подчиненного суждения «Некоторые адвокаты входят в Московскую коллегию адвокатов» подчиняющее суждение «Все адвокаты входят в Московскую коллегию адвокатов» будет ложным или истинным.
При ложности подчиненного суждения «Некоторые адвокаты не входят в Московскую коллегию адвокатов» (О) будет ложным подчиняющее суждение «Ни один адвокат не входит в Московскую коллегию адвокатов» (Е). Но при ложности подчиняющего суждения «Ни один адвокат не входит в Московскую коллегию адвокатов» (Е) подчиненное суждение «Некоторые адвокаты не входят в Московскую коллегию адвокатов» (О) будет истинным или ложным.
Отношения противоречия существует между общеутвердительными и частноотрицательными суждениями (А - О) и между общеотрицательными и частноутвердительными суждениями (Е - I). Сущность этого отношения состоит в том, что из двух противоречающих суждений одно обязательно истинно, другое - ложно. Два противоречивых суждения не могут быть ни одновременно истинными, ни одновременно ложными.
Умозаключения, основанные на отношении противоречия, называются отрицанием простого категорического суждения. С помощью отрицания суждения из исходного суждения образуется новое суждение, являющееся истинным, когда исходное суждение (посылка) ложно, и ложным, когда исходное суждение (посылка) истинно. Например, отрицая истинное суждение «Все адвокаты - юристы» (А), мы получим новое, ложное, суждение «Некоторые адвокаты не есть юристы» (О). Отрицая ложное суждение «Ни один адвокат не юрист» (Е), мы получим новое, истинное, суждение «Некоторые адвокаты - юристы» (I).
Знание зависимости истинности или ложности одних суждений от истинности или ложности других суждений помогает делать правильные выводы в процессе рассуждения.
17) Сложным называют суждение, состоящее из нескольких простых, связанных логическими связками. Различают следующие виды сложных суждений: 1) соединительные, 2) разделительные, 3) услов-| ные, 4) эквивалентные. Истинность таких сложных суждений определяется истинностью составляющих их простых.Соединительным, или конъюнктивным называют суждение, со' стоящее из нескольких простых, связанных логической связкой «и». Разделительным, или дизъюнктивным, называют суждение, ее стоящее из нескольких простых, связанных логической связко «или». Условным, или импликативным, называют суждение, состоя* щее из двух простых, связанных логической связкой «если.., то...».,
4. Эквивалентные суждения (двойная импликация). Эквивалентным называют суждение, включающее в качесг.^ составных два суждения, связанных двойной (прямой и обратной^ условной зависимостью, выражаемой логической связкой «если i только если..., то..
.». Например: «Если и только если человек на гражден орденами и медалями (р), то он имеет право на ношеш соответствующих орденских планок (q)».
18) УМОЗАКЛЮЧЕНИЕ — мыслительный процесс, в ходе которого из одного или нескольких суждений, называемых посылками, выводится новое суждение, называемое заключением, или следствием. Структура умозаключения обусловлена природой этой формы мышления.
В структуре умозаключения различают два основных более или менее сложных элемента: посылки (одна или несколько) и заключение, между которыми, конечно, существует определенная связь.
Посылки – это исходное, уже известное знание, служащее основанием для умозаключения.
Заключение (или вывод) – производное и притом новое знание, полученное из посылок и выступающее их следствием.
Связь между посылками и умозаключением есть необходимое отношение между ними, делающее возможным переход от одного к другому, – отношение логического следования.
Если мы признаем какие-либо посылки, то мы вынуждены признать и заключение – именно из-за определенной связи между тем и другим, а также между самими посылками. Это закон, в основе которого лежит объективное соотношение самих предметов мысли, он проявляется во многих особых правилах, которые специфичны для разных видов умозаключений.
19) В определении дедукции в логике выявляются два подхода:
1. В традиционной (не в математической) логике дедукцией называют умозаключение от знания большей степени общности к новому знанию меньшей степени общности. Впервые теория дедукции в этом плане была обстоятельно разработана Аристотелем;
2. В современной математической логике дедукцией называется умозаключение, дающее достоверное (истинное) суждение. Четкая фиксация существенного различия классического и современного понимания дедукции особенно важна для решения методологических вопросов. Для различения двух смыслов дедукции можно классическое понимание обозначить термином “дедукция1” (сокращенно Д1), а современное - “дедукция2” (Д2). Правильно построенному дедуктивному умозаключению присущ необходимый характер логического следования заключения из данных посылок. Обобщая сказанное, можно дать такое определение.
Дедуктивные умозаключения - те умозаключения, у которых между посылками и заключением имеется отношение логического следования.
Определение дедуктивного умозаключения, данного в традиционной логике (т. е. Д1), - частный случай этого определения через логическое следование. Рассмотрим пример:
Все перепончатокрылые - насекомые.
Все пчелы - перепончатокрылые.
Все пчелы - насекомые.
Здесь первая посылка “Все перепончатокрылые - насекомые” является общеутвердительным суждением и выражает большую степень обобщения по сравнению с заключением, также являющимся общеутвердительным суждением: “Все пчелы - насекомые”. Мы строим умозаключение от признака, принадлежащего роду (“перепончатокрылые”), к его принадлежности к виду - “пчела”, т. е. от общего класса к его частному случаю, к подклассу. Частный случай при этом не надо путать с частными суждениями вида “Некоторые S суть Р” или “Некоторые S не суть Р”.
-------Логический переход от знания об отдельных явлениях к знанию общему совершается в этом случае в форме индуктивного умозаключения, или индукции (от латинского inductio — «наведение»).
Индуктивным называется умозаключение, в котором на основании принадлежности признака отдельным предметам или частям некоторого класса делают вывод о его принадлежности классу в целом.
В истории денежной единице США, например, было установлено, что доллар неплохо обращается, а Америке, Европе, Азии и Австралии. Учитывая принадлежность этих частей света можно сделать индуктивное умозаключение, что доллар – он и в Африке доллар.
В основе логического перехода от посылок к заключению в индуктивном выводе лежит подтверждаемое тысячелетней практикой положение о закономерном развитии мира, всеобщем характере причинной связи, проявлении необходимых признаков явлений через их всеобщность и устойчивую повторяемость. Именно эти методологические положения оправдывают логическую состоятельность и эффективность индуктивных выводов.
Основная функция индуктивных выводов в процессе познания —генерализация, т.е. получение общих суждений. По своему содержанию и познавательному значению эти обобщения могут носить различный характер — от простейших обобщений повседневной практики до эмпирических обобщений в науке или универсальных суждений, выражающих всеобщие законы.
----------Термин «аналогия» в древнегреческом языке означал пропорцию. Первоначально он использовался древнегреческими математиками для обозначения совпадения отношения между числами. Система двух чисел 6 и 9 «аналогична» системе двух чисел 8 и 12, поскольку отношения соответствующих членов этих двух систем согласуются: 6: 9=8: 12.
В логике аналогия рассматривается как форма получения выводного знания, как умозаключения, в котором на основании сходства предметов в одних признаках делается вывод о сходстве этих предметов в других признаках. Пример из практики научного познания: в спектрах химических элементов, удаленных от Земли, линии туманностей сдвинуты в сторону красной части спектра по сравнению с линиями этих элементов, наблюдаемых в земных условиях. Это – явление «красного смещения». «Красное смещение» - результат взаимного удаления галактик в окружающей нас области Вселенной. Явление «красного смещения» было открыто по аналогии с акустическими явлениями, так называемым «эффектом Доплера». Частота колебаний или длина звуковой волны, воспринимаемая наблюдателем, изменяется в зависимости от движения источника звука и наблюдателя относительно друг друга. При их сближении частота возрастает, при удалении – уменьшается. В акустике при сближении источника звука и приемника-наблюдателя тон звука повышается, при удалении - понижается. Сходство природы света и звука в ряде свойств послужило основанием для истолкования «красного смещения» по аналогии с эффектом Доплера, как следствие удаление от нас туманностей. Смысл аналогии заключается в том, чтобы находить неизвестные признаки предмета, опираясь на ранее приобретенные знания о другом, сходном с ним предмете, переносить информацию от одного предмета на другой на основе некоторого соотношения между ними.
Умозаключения по аналогии - это вывод о принадлежности единичному предмету определенного признака, основанный на сходстве этого предмета в существенных признаках с другим единичным предметом.
Вывод в умозаключении по аналогии можно представить следующей схемой:
A имеет признаки: a, b, c, d, e……….
B имеет признаки a, b, c, d……….
Следовательно, В, по-видимому, имеет признак e.
А и В в этой схеме – сравниваемые предметы, a, b, c, d, - сходные для обоих предметов признаки, e – признак, присущий А и в силу сходства между предметами переносимый на В.
Аналогия, как и вся логическая фигура, не является произвольным логическим построением. В ее основе лежат объективные свойства и отношения предметов реальной действительности.
20) Умозаключение — это способ получения нового знания на основе некоторого имеющегося.
Этот способ представляет собой переход от некоторых высказываний, фиксирующих наличие некоторых ситуаций в действительности, к новому высказыванию и соответственно к знанию о наличии ситуации, которую описывает это высказывание.
Переход от некоторых высказываний (посылок умозаключения) к высказыванию (заключению) в умозаключении может совершаться на основе интуитивного усмотрения какой-то связи - такие умозаключения называют содержательными; или путем логического выведения одного высказывания из других - это умозаключения формально-логического характера. В первом случае оно представляет собой, по существу, психический акт. Во втором случае его можно рассматривать как определенную логическую операцию. Последняя и является предметом изучения логики.
В содержательных умозаключениях мы оперируем, по существу, не с самими высказываниями, а прослеживаем связь между ситуациями действительности, которые эти высказывания представляют. Это и отличает содержательные умозаключения от умозаключений как операций логического характера, называемых иногда формализованными умозаключениями. В этих умозаключениях операции совершаются именно над высказываниями самими по себе, причем по правилам, которые вообще не зависят от конкретного содержания высказываний. Для содержательных умозаключений нет никаких определенных критериев этого рода и всегда возможен спор - рассуждает ли человек правильно или нет. Именно формализованные умозаключения являются предметом изучения логики. И именно их мы имеем в виду в дальнейшем.
В умозаключении, как мы уже говорили, различают посылки - высказывания, представляющие исходное знание, и заключение - высказывание, к которому мы приходим в результате умозаключения.
В естественном языке существуют слова и словосочетания, указывающие как на заключение («значит», «следовательно», «отсюда видно», «поэтому»), так и на посылки умозаключения («так как», «поскольку», «ведь»). Представляя суждение в некоторой стандартной форме, в логике принято указывать вначале посылки, а потом заключение, хотя в естественном языке их порядок может быть произвольным: вначале заключение - потом посылки; заключение может находиться «между посылками».
Понятие умозаключения как логической операции тесно связано с понятием логического следования. Учитывая эту связь, мы различаем правильные и неправильные умозаключения.
Умозаключение, представляющее собой переход от посылок к заключению, является правильным, если между посылками и заключением имеется отношение логического следования. В противном случае - если между посылками и заключением нет такого отношения - умозаключение неправильно.
В делении умозаключений на правильные и неправильные мы должны различать отношение логического следования двух видов – дедуктивное и индуктивное. Первое гарантирует истинность заключения при истинности посылок. Второе - при истинности посылок - обеспечивает лишь некоторую степень правдоподобия заключения (некоторую вероятность его истинности). Соответственно этому умозаключения делятся на дедуктивные и индуктивные. Первые иначе еще называют демонстративными (достоверными), а вторые - правдоподобными (проблематичными).
21) Простой категорический силлоги́ зм (греч. σ υ λ λ ο γ ι σ μ ό ς) — рассуждение мысли, состоящее из трёх простых атрибутивных высказываний: двух посылок и одного заключения. Посылки силлогизма разделяются на бо́ льшую (которая содержит предикат заключения) и меньшую (которая содержит субъект заключения). По положению среднего термина силлогизмы делятся на фигуры, а последние по логической форме посылок и заключения — на модусы.
Пример силлогизма:
Всякий человек смертен (бо́ льшая посылка)
Сократ — человек (меньшая посылка)
------------
Сократ смертен (заключение)
22) Правила простого категорического силлогизма
·Средний термин должен быть распределён хотя бы в одной из посылок.
·Термин, не распределённый в посылке, не должен быть распределён в заключении.
·Число отрицательных посылок должно быть равно числу отрицательных заключений.
·В каждом силлогизме должно быть только три термина
Правила терминов:
1) в силлогизме должно быть три термина
2) средний термин должен быть распределен, хотя бы в одной из посылок
3) термин, не распределенный в посылке, не может быть распределн в заключении
Правила посылок:
1)из двух отрицательных, так же как и частных посылок нельзя сделать никакого заключения
2) если одна из посылок отрицательное или частное суждение, то и заключение должно быть соответственно, отрицательным или частным суждением.
3) Хотя бы одна из посылок должна быть утвердительным суждением.
Адвокаты не судьи.
Студенты не адвокаты.
?
2. Если одна из посылок - отрицательное суждение, то и заключение - отрицательное суждение.
Все адвокаты юристы.
Петров не юрист.
Петров не адвокат.
3. Хотя бы одна из посылок должна быть общим суждением.
Некоторые юристы спортсмены.
Некоторые юристы любят музыку.
?
4. Если одна из посылок частная, то и заключение должно быть частным.
Все преступники должны быть наказаны.
Некоторые люди - преступники.
4)
23) Фигуры и правила фигур силлогизма. В зависимости от места среднего термина в посылках различают четыре фигуры категорического силлогизма.
Первая фигура - разновидность силлогизма, в которой средний термин занимает место субъекта в большей посылке (М - Р) и место предиката в меньшей посылке (S - М). Например:
Все адвокаты (М) - юристы (Р)
Петров (S) - адвокат (М).
Петров (S) - юрист (Р).
М-Р - большая посылка.
S - М - меньшая посылка.
S — Р - заключение.
Правила первой фигуры:
Ø большая посылка должна быть общим суждением (А, Е);
Ø меньшая посылка должна быть утвердительным суждением (А, I).
Первая фигура силлогизма широко применяется в юридической науке и практике. Так, по первой фигуре производится квалификация различных правовых явлений, преступлений, фактов судебной практики. При этом большей посылкой выступает та или иная статья кодекса, правовая норма, закон, а меньшей - рассматриваемый конкретный случай. В заключении делается вывод о рассматриваемом случае на основании общего положения. Например, «Тайное хищение чужого имущества составляет кражу. Данный человек совершил тайное хищение чужого имущества. Следовательно, данный человек совершил кражу».
Вторая фигура - разновидность простого силлогизма, в которой средний термин занимает место предиката в обеих посылках.
Например:
Все адвокаты (М) - юристы.
Петров - не юрист (М).
Петров - не адвокат.
Р - М - большая посылка.
S - М - меньшая посылка.
S — Р - заключение.
Правила второй фигуры:
Ø большая посылка должна быть общим суждением (А, Е);
Ø одна из посылок должна быть отрицательной (Е, О).
Вторая фигура применяется при доказательствах ложности какого-либо положения путем отрицания принадлежности исследуемых предметов к классу предметов, о которых мыслится в большей посылке. В судебной практике данная фигура служит для логического обоснования отсутствия состава преступления в том или ином конкретном деянии, для доказательства неправильной квалификации преступления, для опровержения каких-либо положений, не согласующихся с общим правилом. Например, «Этот смертельный удар нанесен человеком, обладающим огромной физической силой. Обвиняемый не является человеком, обладающим огромной физической силой. Следовательно, обвиняемый не мог нанести этот смертельный удар».
Третья фигура - разновидность силлогизма, в которой средний термин занимает место субъекта в обеих посылках (М - Р; М -S). Например:
Все подозреваемые (М) признали свою вину.
Все подозреваемые (М) привлечены к уголовной ответственности.
Некоторые привлеченные к уголовной ответственности, признали свою вину.
М - Р - большая посылка.
М - S - меньшая посылка.
S - Р - заключение.
Правила третьей фигуры:
Ø меньшая посылка должна быть утвердительным суждением (А, I);
Ø о заключение должно быть частным суждением (I, О).
Третья фигура служит чаще всего для установления частичной совместимости признаков, относящихся к одному и тому же предмету. Она также может быть применима для опровержения отдельных общих положений. Например, необходимо опровергнуть суждение «Ни один свидетель не дал правдивых показаний» (т. е. доказать противоречащее ему суждение «Некоторые свидетели дали правдивые показания») и известно, что свидетели X. и Y. дали правдивые показания. Построим умозаключение по третьей фигуре:
X. и Y. (М) - дали правдивые показания.
X. и Y. (M) - свидетели.
Некоторые свидетели дали правдивые показания.
P - M- большая посылка.
S - M - меньшая посылка.
S-P- заключение.
Поскольку частноутвердительное суждение «Некоторые свидетели дали правдивые показания» является истинным, то находящееся с ним в отношении противоречия общеотрицательное суждение «Ни один свидетель не дал правдивых показаний» - ложное.
Четвертая фигура - разновидность силлогизма, в которой средний термин занимает место предиката в большей и место субъекта в меньшей посылке (Р - M, M - S), схематично выражается:
Р - М - большая посылка.
М - S - меньшая посылка.
S - Р - заключение.
Четвертая фигура силлогизма практически не употребляется.
По первой фигуре можно получить выводы из всех основных видов суждений. Вторая фигура дает только отрицательный вывод. В третьей фигуре вывод будет частным суждением.
В зависимости от того, какие суждения по количеству и качеству составляют простой категорический силлогизм (являются посылками и заключением), различают виды силлогизмов, которые называют модусами. Модусы простого категорического силлогизма - это его разновидности, отличающиеся друг от друга качественной и количественной характеристикой входящих в них посылок и заключения.
В четырех фигурах силлогизма максимальное число комбинаций равно 64. Однако правильных модусов всего 19:
Первая фигура: ААА, ЕАЕ, АII, ЕIО
Вторая фигура: ЕАЕ, АЕЕ, ЕIО, АОО
Третья фигура: AAI, IAI, АII, ЕАО, ОАО, ЕIО
Четвертая фигура: AAI, АЕЕ, IAI, ЕАО, ЕIО
В соответствии с этим называют модусы первой фигуры, модусы второй фигуры и т. д. Например, модус ААА 1-й фигуры, модус АЕЕ 2-й фигуры и т.д. Все другие модусы возможны, но они являются неправильными, так как в них нарушаются те или иные правила категорического силлогизма. Знание модусов дает возможность определить форму истинного заключения, когда даны посылки и известно, какова фигура данного силлогизма.
Знания специальных правил фигур являются производными от перечисленных выше общих правил силлогизма. Главная трудность при проверки правильности того или иного силлогизма состоит в том, чтобы правильно построить умозаключение. Правила простого категорического силлогизма не позволяют определить содержание посылок, но они указывают, каким требованиям эти посылки должны удовлетворять, чтобы их можно было связать между собой и сделать необходимое заключение.
Но умозаключения строятся не только из простых, но и из сложных суждений. Широко используются умозаключения, посылками которых являются условные и разделительные суждения, выступающие в разных сочетаниях друг с другом или с категорическими суждениями.
24) В четырех фигурах силлогизма максимальное число комбинаций равно 64. Однако правильных модусов всего 19:
Первая фигура: ААА, ЕАЕ, АII, ЕIО
Вторая фигура: ЕАЕ, АЕЕ, ЕIО, АОО
Третья фигура: AAI, IAI, АII, ЕАО, ОАО, ЕIО
Четвертая фигура: AAI, АЕЕ, IAI, ЕАО, ЕIО
В соответствии с этим называют модусы первой фигуры, модусы второй фигуры и т. д. Например, модус ААА 1-й фигуры, модус АЕЕ 2-й фигуры и т.д. Все другие модусы возможны, но они являются неправильными, так как в них нарушаются те или иные правила категорического силлогизма. Знание модусов дает возможность определить форму истинного заключения, когда даны посылки и известно, какова фигура данного силлогизма.
Знания специальных правил фигур являются производными от перечисленных выше общих правил силлогизма. Главная трудность при проверки правильности того или иного силлогизма состоит в том, чтобы правильно построить умозаключение. Правила простого категорического силлогизма не позволяют определить содержание посылок, но они указывают, каким требованиям эти посылки должны удовлетворять, чтобы их можно было связать между собой и сделать необходимое заключение.
Но умозаключения строятся не только из простых, но и из сложных суждений. Широко используются умозаключения, посылками которых являются условные и разделительные суждения, выступающие в разных сочетаниях друг с другом или с категорическими суждениями.
25) Сведение модусов рассматривается как процедура их
доказательства, так как только модусы I фигуры соответствуют аксиоме
силлогизма, а последняя, поскольку она аксиома, не требует
доказательства.
Латинские мнемонические названия правильных модусов:
I Barbara, Celarent, Darii, Ferio
II Cesare, Camestres, Festino, Baroco
III Darapti, Disamis, Datisi, Bocardo, Felapton, Ferison
IV Bramantip, Camenes, Dimaris, Fesapo, Fresison
В этих названиях начальные буквы указывают на тот модус I
фигуры, к которому сводится данный модус, например, Datisi сводится
к Darii. Буква s означает, что гласная, стоящая перед этой буквой,
обозначает суждение, которое подлежит чистому обращению, к
примеру, в модусе Cesare. Буква m указывает на то, что посылки
следует поменять местами, например, в модусе Dimaris. Буква p
означает, что гласная, стоящая перед этой буквой, обозначает
суждение, которое подлежит обращению с ограничением: Fesapo.
Буква c указывает на то, что данный модус сводится к модусу I
фигуры при помощи метода приведения к абсурду с использованием
модуса Barbara.
Таким образом доказываются два модуса: Baroco, Bocardo.
Пример: свести модус Camestres второй фигуры к модусу Celarent
первой фигуры.
Camestres
P a M Все рыбы дышат жабрами
S e M Киты не дышат жабрами
S e P Киты не есть рыбы
Celarent
P a M P a M m) → M e S M e S
S e M s) → M e S P a M P a M
_____ _____ _____ _____
S e P P e S s) → S e P
Celarent I ф. Ни один из дышащих жабрами не есть кит
Все рыбы дышат жабрами
Киты не есть рыбы
Пример с использованием метода приведения к абсурду:
Bocardo III фигуры
М о Р Не все музыканты - композиторы
М а S Все музыканты обладают хорошим слухом
______ _______________________________________
S о Р Некоторые люди, обладающие хорошим слухом не являются
композиторами.
Предположим, что заключение S o P неверно. Тогда верно
(вспомним логический квадрат) противоречащее ему суждение
26) Для простоты применения и экономии времени, а особенно в случаях, когда заключение очевидно, применяются сокращенные силлогизмы. Когда говорится о сокращенных силлогизмах, имеется в виду, что в таком умозаключении пропущена одна из посылок, а в некоторых случаях — заключение.
В мышлении мы оперируем понятиями, суждениями и умозаключениями, в том числе и силлогизмами. Как и суждения, силлогизм может быть простым (рассмотрен выше) и сложным. Конечно, слово «сложный» не стоит понимать в обычном смысле слова, как «тяжелый» или «трудный». Сложный силлогизм состоит из нескольких простых силлогизмов. Они образуют полисиллогизм, или сложный силлогизм; это синонимы. Полисиллогизм представляет собой несколько соединенных между собой последовательной связью простых силлогизмов. При этом вывод, следствие одного из простых силлогизмов становится посылкой для последующего. Таким образом, получается своеобразная «цепь» силлогизмов.
Все полисиллогизмы делятся на регрессивные и прогрессивные. Прогрессивный силлогизм характеризуется тем, что его заключение становится большей посылкой следующего силлогизма.
Заключение регрессивного силлогизма становится меньшей посылкой в последующем.
В указанных случаях восстановление силлогизма достаточно просто, однако иногда возникают проблемы с определением посылки и заключения и их отделением друг от друга. Поэтому нужно иметь в виду, что перед посылкой обычно стоят слова «так как», «потому что» и др. Перед заключением обычно ставят такие слова, как «следовательно» или «поэтому».
Так как сокращенный силлогизм удобен и компактен, он используется чаще, чем полные категорические силлогизмы. Сокращенный категорический силлогизм также называют энтимемой.
Среди сложносокращенных силлогизмов выделяют эпихейремы и сориты. Начать следует с соритов, так как их понятие используется при рассмотрении второго вида. Так же как и сложные силлогизмы, сориты бывают прогрессивными и регрессивными. Прогрессивные сориты получаются из прогрессивных сложных силлогизмов, регрессивные — из регрессивных. Как было сказано выше, одну из посылок сложного силлогизма составляет заключение предыдущего. При сокращении сложного силлогизма в форму сорита эта посылка пропускается. Может быть пропущена также сложная посылка последующего суждения в полисиллогизме.
Прогрессивный сорит содержит предикат заключения и его субъект. Первым он начинается, а вторым заканчивается. В отличие от прогрессивного регрессивный сорит начинается не с предиката заключения, а с его субъекта. Предикатом же он заканчивается.
|
|
