Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Решение. Имеем систему (М/М/1): (GD/ / ) с параметрами , клиентов в час.

Имеем систему (М/М/ 1): (GD / 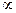/ 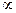) с параметрами 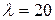, 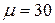клиентов в час.

Найдем сначала операционные характеристики системы.

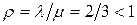– система войдет в стационарный режим.

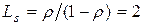человека;

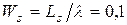часа = 6 минут; 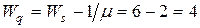минуты;

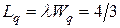человека; ; .

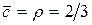Чтобы очередному клиенту досталось сидячее место, нужно, чтобы в тот момент времени, когда он подойдет к банкомату, в системе было от одного до двух человек. Вероятность p этого события равна

.

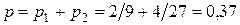Вероятность того, что очередной клиент не будет стоять в очереди равна .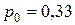

Тогда в среднем 70% клиентов банкомата будут дожидаться своей очереди сидя или вовсе в ней не стоять, а 30% придется ждать стоя. При этом банкомат простаивает без клиентов 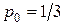всего времени работы. Вероятность того, что очередной клиент банкомата станет в очередь, равна .

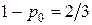Распределение времени нахождения в системе (М/М/1): (FIFO/ / )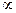

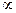Здесь мы определим закон распределения случайной величины Т – времени нахождения в системе очередного прибывшего клиента. Поток клиентов – простейший; время обслуживания имеет показательное распределение с параметром 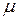, в наличии только один канал обслуживания.

Функция плотности вероятности случайной величины 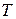такова:

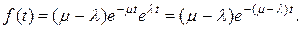
Перед нами показательное распределение с параметром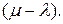