
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Операционные характеристики работы СМО.
|
|
При выполнении условий стационарности нас будут интересовать следующие показатели работы СМО, они называются операционными характеристиками.
 – вероятность того, что в системе находится n клиентов;
– вероятность того, что в системе находится n клиентов;
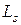 – среднее число находящихся в системе клиентов;
– среднее число находящихся в системе клиентов;
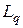 – среднее число клиентов в очереди на обслуживание;
– среднее число клиентов в очереди на обслуживание;
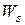 – средняя продолжительность пребывания клиента в системе;
– средняя продолжительность пребывания клиента в системе;
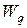 – средняя продолжительность пребывания клиента в очереди.
– средняя продолжительность пребывания клиента в очереди.
По определению математического ожидания
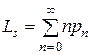 ;
; 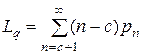 . (19)
. (19)
Здесь с – число каналов обслуживания.
Тогда 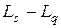 – это среднее число занятых каналов обслуживания, обозначим его
– это среднее число занятых каналов обслуживания, обозначим его 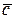 , тогда произведение
, тогда произведение 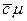 - средняя частота выходного потока обслуженных заявок. С другой стороны
- средняя частота выходного потока обслуженных заявок. С другой стороны 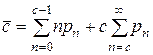 .
.
Но при установившемся режиме работы СМО, когда операционные характеристики не зависят от времени, среднее число заявок, поступающих в систему в единицу времени должно равняться среднему числу заявок, выбывающих из системы в единицу времени.
В противном случае число клиентов в системе в момент времени t будет зависеть от t.
Таким образом, должно выполняться равенство
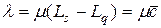 или
или 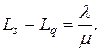 (20)
(20)
Если средняя скорость обслуживания одного канала равна 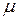 клиентов в единицу времени, то средняя продолжительность обслуживания одного клиента равна
клиентов в единицу времени, то средняя продолжительность обслуживания одного клиента равна  , поэтому
, поэтому
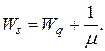 (21)
(21)
Если в очереди 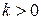 клиентов (в системе
клиентов (в системе 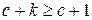 заявок), то среднее время пребывания в очереди последнего стоящего в ней клиента равно
заявок), то среднее время пребывания в очереди последнего стоящего в ней клиента равно 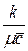 . Чтобы последняя заявка покинула очередь, должны быть обслужены
. Чтобы последняя заявка покинула очередь, должны быть обслужены 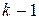 заявок из очереди и одна из тех, кто уже обслуживается. Это – условное математическое ожидание, а безусловное среднее время нахождения в очереди равно
заявок из очереди и одна из тех, кто уже обслуживается. Это – условное математическое ожидание, а безусловное среднее время нахождения в очереди равно
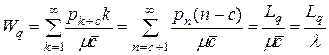 или
или
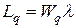 . (22)
. (22)
Отсюда
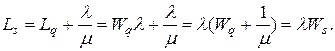
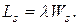 (23)
(23)
Формулы 22 и 23 в литературе по теории массового обслуживания называются формулами Литтла.
Если не каждая из поступивших заявок допускается в СМО из-за того, что блок ожидания имеет ограниченную вместимость, вместо параметра 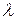 рассматривается величина
рассматривается величина 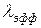 - среднее количество заявок, действительно допускаемых в блок ожидания СМО в единицу времени. Тогда в формулах 20, 22, 23 вместо
- среднее количество заявок, действительно допускаемых в блок ожидания СМО в единицу времени. Тогда в формулах 20, 22, 23 вместо 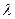 следует писать
следует писать 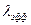 :
:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
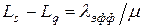 ;
; 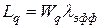 ;
; 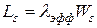 . (24)
. (24)
Ясно, что 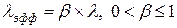 .
.
|
|
