Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Дифференцирование СП

Дано: X(t), m_X(t), R_X(t, t¢)

Y(t)=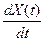

Определить: m_Y(t)=? R_Y(t, t¢)=?

m_Y(t)= 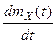. Действительно, m_Y(t)= .=

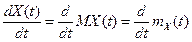R_Y(t, t¢)= .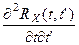

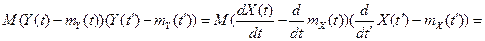
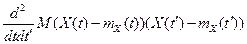
Интегрирование СП

Дано: X(t), m_X(t), R_X(t, t¢)

Y(t)=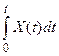

Определить: m_Y(t)=? R_Y(t, t¢)=?

m_Y(t)=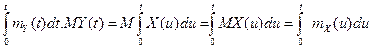

R_Y(t, t¢)=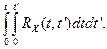

=

=

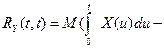
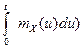
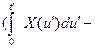
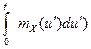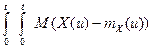
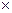
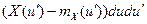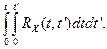
Стационарные СП

Процесс X(t) называется стационарным в широком смысле, если его математическое ожидание 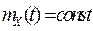не зависит от времени, а корреляционная функция зависит только

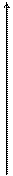от разности аргументов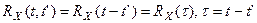

Свойства R_X(t):

1) R_X(t)=R_X(-t) - симметрия относительно оси ординат R_X(t)

(четность)

2) max ê R_X(t)÷ =R_X(0)

t

0 t

Свойства эргодичности стационарных СП

Усреднение по ансамблю реализаций: x(t)x(t)

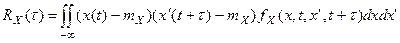
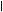
Усреднение по одной реализации:

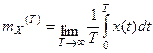t t t+ t T t

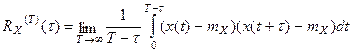
Эргодичность по МО

X(t) - обладает свойством эргодичности по М.О., если с вероятностью равной 1 имеем

m_X^(T)=m_X