Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Корреляционная функция СП

Классификация СП

Случайные процессы

Дискретные СП Непрерывные СП

а) непрерывные по времени а) непрерывные по времени

б) дискретные по времени б) дискретные по времени

Характеристики СП

Математическое ожидание (МО) СП

Математическим ожиданием случайного процесса X(t) называется неслучайная функция времени m_x(t), которая при каждом значении аргумента t=t¢ равна математическому ожиданию СВ X(t¢), соответствующей этому сечению процесса X(t).

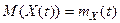
(если X(t) – непрерывный СП)

f_x(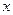, t) – одномерная плотность распределения X(t).

Корреляционная функция СП

Корреляционной функцией или автокорреляционной случайного процесса X(t) называется неслучайная функция R_x(t, t¢) двух переменных t и t¢, значение которой при всяких t и t¢ равно ковариации случайных величин

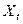и , соответствующих этим сечениям процесса X(t).

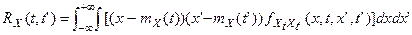, где X(t) – непрерывный СП;

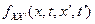- двумерная плотность распределения случайного процесса X(t).

Корреляционная функция – сечения относятся к одному СП. Корреляционная функция характеризует степень линейной связи СВ, соответствующих двум сечениям СП. Если X_t и X_t¢ независимы, то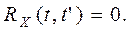

Для окорреляционной функции справедливо R_X(t, t¢) = R_X(t¢, t).

Взаимно корреляционная функция – берутся сечения двух разных СП: X(t) и Y(t).

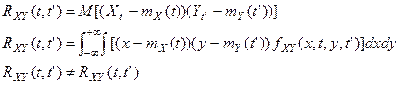
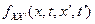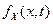
Для независимых СП = 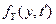. Отсюда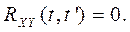