
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Форма и размеры Земли
|
|
Санкт-Петербург
Издательство Политехнического университета
УДК 528.48(075.8)
Инженерная геодезия. Решение инженерных задач на планах и картах: Учеб. пособие / Н.Д. Беляев, Ф.Н. Духовской, Н.Н. Загрядская, Е.Б. Михаленко. СПб.: Изд-во Политехн. ун-та, 2004. 66 с.
Пособие соответствует государственному стандарту по направлению 550100 «Строительство».
Приведены основные сведения о современных топографических картах. Даны характеристики карт и планов, рассмотрены способы изображения рельефа, контуров и объектов местности, различные системы координат, применяемые в геодезии, номенклатура топографических карт и планов.
Подробно изложена методика измерений по картам. Рассматриваются определение высот (отметок) и плановых координат точек, построение профилей, измерение площадей. Даются способы математической обработки результатов геодезических измерений и оценки их точности.
Предназначено для студентов инженерно-строительного факультета в пределах программы бакалавриата.
Табл. 2. Ил. 51. Библиогр.: 5 назв.
Печатается по решению редакционно-издательского совета Санкт-Петербургского государственного политехнического университета.
ã Санкт-Петербургский государственный
политехнический университет, 2004
ВВЕДЕНИЕ
Структуру и содержание учебного пособия определили программа, общий лимит времени, который отводится на дисциплину «Инженерная геодезия» на инженерно-строительном факультете (порядка 100 часов), принятая лекционно-практическая форма обучения.
Лекционно-практический метод предусматривает такую форму обучения, когда положения теории во всех необходимых случаях сразу же закрепляются практическими упражнениями – решением задач, выполнением работ. При этом, в зависимости от содержания темы, решение отдельных задач выполняется преподавателем. Соответственно в тексте приведены рекомендуемые задачи. В других случаях после законченного изложения теории вопроса практическая часть приводится в конце параграфа. Здесь предусматривается самостоятельная работа студентов, но с помощью и под контролем преподавателя.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Комплексное освоение материала курса осуществляется при самостоятельном выполнении студентами расчетно-графических работ.
ФОРМА И РАЗМЕРЫ ЗЕМЛИ
Общая форма Земли, как материального тела, определяется действием внутренних и внешних сил на ее частицы. Если бы Земля была неподвижным однородным телом и подвергалась действию только внутренних сил тяготения, она имела бы форму шара. Действие центробежной силы, вызванной вращением Земли вокруг ее оси, определяет сплюснутость Земли у полюсов. Под воздействием внутренних и внешних сил физическая (топографическая) поверхность Земли образует фигуру неправильной, сложной формы. Одновременно на физической поверхности Земли встречаются самые различные неровности: горы, хребты, долины, котловины и т. д. Описать такую фигуру при помощи каких-либо аналитических зависимостей невозможно. В то же время для решения геодезических задач в конечном виде необходимо основываться на определенной математически строгой фигуре – только тогда возможно получение расчетных формул. Исходя из этого задачу по определению формы и размеров Земли принято делить на две части:
1) установление формы и размеров некоторой типичной фигуры, представляющей Землю в общем виде;
2) изучение отступлений физической поверхности Земли от этой типичной фигуры.
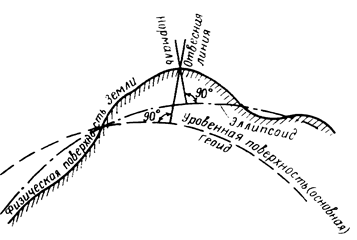
Известно, что 71 % земной поверхности покрывают моря и океаны, суши – только 29 %. Поверхность же морей и океанов характерна тем, что она в любой точке перпендикулярна к отвесной линии, т.е. направлению действия силы тяжести (если вода находится в спокойном состоянии). Направление действия силы тяжести можно установить в любой точке и соответственно построить поверхность, перпендикулярную к направлению этой силы. Замкнутая поверхность, которая в любой точке перпендикулярна к направлению действия силы тяжести, т.е. перпендикулярна к отвесной линии, называется уровенной поверхностью.
Уровенная поверхность, совпадающая со средним уровнем воды в морях и океанах в их спокойном состоянии и мысленно продолженная под материками, называется основной (исходной, нулевой) уровенной поверхностью. В геодезии за общую фигуру Земли принимают фигуру, ограниченную основной уровенной поверхностью, и такую фигуру именуют геоидом (рис. 1).
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
|
|
| Рис. 1 | Рис. 2 |
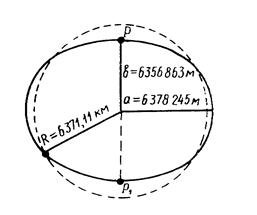
Вследствие особой сложности, геометрической неправильности геоида, его заменяют другой фигурой – эллипсоидом, образующимся при вращении эллипса вокруг его малой оси РР 1(рис. 2). Размеры эллипсоида определялись неоднократно учеными ряда стран. В Российской Федерации они были вычислены под руководством профессора Ф.Н. Красовского в 1940 г. и в 1946 г. постановлением Совета Министров СССР были утверждены: большая полуось а = 6 378 245 м, малая полуось b = 6 356 863 м, сжатие
 .
.
Земной эллипсоид ориентируют в теле Земли так, чтобы его поверхность в наибольшей мере соответствовала поверхности геоида. Эллипсоид с определенными размерами и определенным образом ориентированный в теле Земли называется референц-эллипсоидом (сфероидом).
Наибольшие отклонения геоида от сфероида составляют 100–150 м. В тех случаях, когда при решении практических задач фигуру Земли принимают за шар, радиус шара, равновеликого по объему эллипсоиду Красовского, составляет R = 6 371 110 м = 6371, 11 км.
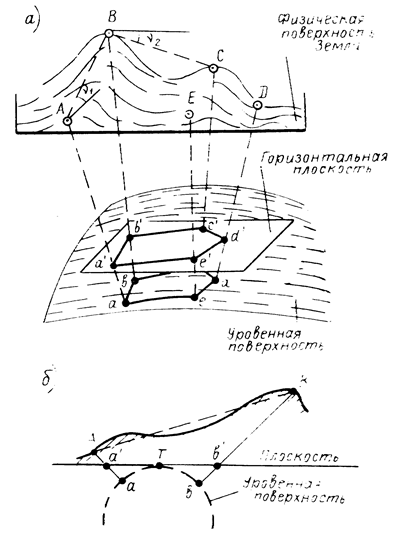
Рис. 3
При решении практических задач в качестве типичной фигуры Земли принимают сфероид или шар, а для небольших участков кривизну Земли вообще не учитывают. Такие отступления целесообразны, так как упрощается проведение геодезических работ. Но эти отступления приводят к искажениям при отображении физической поверхности Земли тем методом, который принято именовать в геодезии методом проекций.
Метод проекций при составлении карт и планов заключается в том, что точки физической поверхности Земли А, В и так далее проектируются отвесными линиями на уровенную поверхность (см. рис. 3, а, б). Точки а, b и так далее называются горизонтальными проекциями соответствующих точек физической поверхности. Затем определяется положение этих точек на уровенной поверхности с помощью различных систем координат, и тогда их можно нанести на лист бумаги, т. е. на лист бумаги будет нанесен отрезок ab, который является горизонтальной проекцией отрезка AВ. Но, чтобы по горизонтальной проекции определить действительное значение отрезка AВ, необходимо знать длины аА и bВ (см. рис. 3, б), т.е. расстояния от точек A и В до уровенной поверхности. Эти расстояния называются абсолютными высотами точек местности.
Таким образом, задача составления карт и планов распадается на две:
определение положения горизонтальных проекций точек;
определение высот точек местности.
При проектировании точек на плоскость, а не на уровенную поверхность, появляются искажения: вместо отрезка ab будет отрезок а'b' вместо высот точек местности аА и bВ будут а'А и b'В (см. рис. 3, а, б).
Итак, длины горизонтальных проекций отрезков и высоты точек будут различны и при проектировании на уровенную поверхность, т.е. при учете кривизны Земли, и при проектировании на плоскость, когда кривизна Земли не учитывается (рис. 4). Эти различия будут наблюдаться в длинах проекций D S = t – S, в высотах точек D h = b'О – bО = b'О – R.
Задача в отношении учета кривизны Земли сводится к следующему: принимая Землю за шар с радиусом R, необходимо определить, для какого наибольшего значения отрезка S можно не учитывать кривизну Земли при условии, что в настоящее время относительная погрешность 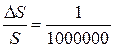 считается допустимой при самых точных измерениях расстояний (
считается допустимой при самых точных измерениях расстояний (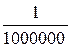 – 1 см на 10 км). Искажение по длине составит
– 1 см на 10 км). Искажение по длине составит
D S = t – S = R tga – R a = R (tga – a). Но, так как S мало по сравнению с радиусом Земли R, то для малого угла можно принять 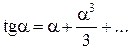 . Тогда
. Тогда 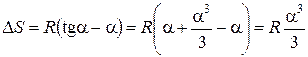 . Ho
. Ho 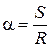 и тогда
и тогда 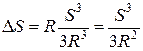 . Соответственно
. Соответственно 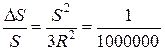 и
и 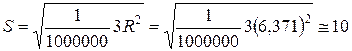 км (с округлением до 1 км).
км (с округлением до 1 км).
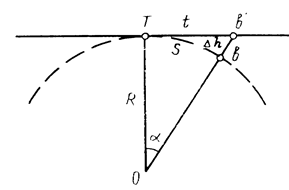
Рис. 4
Следовательно, участок сферической поверхности Земли диаметром в 20 км можно принимать за плоскость, т.е. кривизну Земли в пределах такого участка, исходя из погрешности 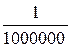 , можно не учитывать.
, можно не учитывать.
Искажение в высоте точки D h = b'О – bО = R seca – R = R (seca – 1). Принимая 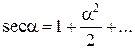 , получаем
, получаем 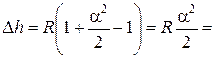
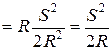 . При разных значениях S получаем:
. При разных значениях S получаем:
| S, км: | 0, 1; | 0, 2; | 0, 3; | 1; | 10; |
| D h, см: | 0, 1; | 0, 3; | 0, 7; | 7, 8; | 784. |
В инженерно-геодезических работах допускаемая погрешность обычно составляет не более 5 см на 1 км, и поэтому кривизну Земли следует учитывать при сравнительно небольших расстояниях между точками, порядка 0, 8 м.
ОБЩИЕ ПОНЯТИЯ О КАРТАХ, ПЛАНАХ И ПРОФИЛЯХ
Главное отличие плана от карты заключается в том, что при изображении участков земной поверхности на плане горизонтальные проекции соответствующих отрезков наносят без учета кривизны Земли. При составлении карт кривизну Земли приходится учитывать.
Практические потребности в точности изображения участков земной поверхности различны. При составлении проектов строительных объектов они значительно выше, чем при общем изучении территории района, геологических обследованиях и т.д.
Известно, что с учетомдопустимой погрешности при измерении расстояний D S = 1 см на 10 км участок сферической поверхности Земли диаметром в 20 км можно принимать за плоскость, т.е. кривизну Земли для такого участка можно не учитывать.
Соответственно создание плана схематически можно представить следующим образом. Непосредственно на местности (см. рис. 3, а) измеряют расстояния АВ, ВС …, горизонтальные углы b1; b2 … и углы наклона линий к горизонту n1, n2 .... Затем от измеренной длины линии местности, например AB, переходят к длине ее ортогональной проекции а'b' на горизонтальной плоскости, т.е. определяют горизонтальное проложение этой линии по формуле а'b' = AB cosn, и, уменьшая в определенное число раз (масштаб), откладывают отрезок а'b' на бумаге. Вычислив аналогичным путем горизонтальные проложения других линий, получают на бумаге многоугольник (уменьшенный и подобный многоугольнику а'b'c'd'е'), который является планом контура местности АВСDЕ.
План – уменьшенное и подобное изображение на плоскости горизонтальной проекции небольшого участка земной поверхности без учета кривизны Земли.
Планы принято подразделять по содержанию и масштабу. Если на плане изображены только местные объекты, то такой план называют контурным (ситуационным). Если дополнительно на плане отображен рельеф, то такой план называют топографическим.
Стандартные масштабы планов 1: 500; 1: 1000; 1: 2000; 1: 5000.
Карты обычно разрабатывают для обширной части земной поверхности, при этом приходится учитывать кривизну Земли. Изображение участка эллипсоида или шара нельзя перенести на бумагу без разрывов. В то же время соответствующие карты предназначаются для решения конкретных задач, например для определения расстояний, площадей участков и т.д. При разработке карт задача состоит не в полном устранении искажений, что невозможно, а в уменьшении искажений и математическом определении их значений с тем, чтобы по искаженным изображениям можно было вычислить действительные величины. Для этого применяют картографические проекции, дающие возможность изображать на плоскости поверхность сфероида или шара по математическим законам, обеспечивающим измерения по карте.
Различные требования к картам определили наличие многих картографических проекций, которые подразделяют на равноугольные, равновеликие и произвольные. В равноугольных (конформных) проекциях сфероида на плоскость сохраняются углы изображаемых фигур, но масштаб при переходе от точки к точке изменяется, что приводит к искажению фигур конечных размеров. Однако небольшие участки карты, в пределах которых изменения масштаба не имеют существенного значения, можно рассматривать и использовать как план.
В проекциях равновеликих (эквивалентных) сохраняется отношение площадей любых фигур на сфероиде и на карте, т.е. масштабы площадей везде одинаковы (при отличающихся масштабах по различным направлениям).
В произвольных проекциях не соблюдается ни равноугольность, ни равновеликость. Они применяются для мелкомасштабных обзорных карт, а также для специальных карт в тех случаях, когда карты обладают каким-либо специфическим полезным свойством.
Карта – построенное по определенным математическим законам, уменьшенное и обобщенное изображение поверхности Земли на плоскости.
Карты принято подразделять по содержанию, назначению и масштабу.
По содержанию карты бывают общегеографические и тематические, по назначению – универсальные и специальные. Общегеографические карты универсального назначения отображают земную поверхность с показом всех ее основных элементов (населенные пункты, гидрография и т.д.). Математическая основа, содержание и оформление специальных карт подчиняются их целевому назначению (карты морские, авиационные и многие другие сравнительно узкого назначения).
По масштабам карты условно делят на три вида:
крупномасштабные (1: 10 000 и крупнее);
среднемасштабные (1: 200 000 – 1: 1 000 000);
мелкомасштабные (мельче 1: 1 000 000).
Карты, подобно планам, бывают контурными и топографическими. В Российской Федерации государственные топографические карты издают в масштабах 1: 1 000 000 – 1: 10 000.
В тех случаях, когда карты или планы используют для проектирования инженерных сооружений, для получения оптимального решения особое значение приобретает наглядность в отношении физической поверхности Земли по какому-либо направлению. Например, при проектировании линейных сооружений (дорог, каналов и т.д.) необходимы: детальная оценка крутизны скатов на отдельных участках трассы, ясное представление о почвенно-грунтовых и гидрологических условиях местности, по которой проходит трасса. Такую наглядность, позволяющую принимать обоснованные инженерные решения, обеспечивают профили.
Профиль – изображение на плоскости вертикального разреза земной поверхности по заданному направлению. Чтобы неровности земной поверхности были более заметными, вертикальный масштаб следует выбирать крупнее горизонтального (обычно в 10–20 раз). Таким образом, как правило, профиль является не подобным, а искаженным изображением вертикального разреза земной поверхности.
|
|
