Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Аналитическое решение

Для определения сопротивления заземления 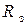необходимо знать потенциал шара. Чтобы найти потенциал шара, применим метод зеркальных изображений. Линии тока заземлителя на поверхности земли не имеют нормальных составляющих, идут вдоль поверхности. Поэтому электрическое поле шара в неоднородной проводящей среде будет аналогично электрическому полю двух шаров в однородной среде в том случае, когда на зеркальном изображении будет ток того же знака, что и на шаровом заземлителе (рис. П2).

Потенциал, создаваемый каждым из шаров в произвольной точке, найдём в предположении, что можно пренебречь искажением поля, вносимым другим шаром, в силу значительно большего расстояния между шарами, чем радиус шара. Окружим уединённый заземлитель сферой радиуса 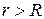. В силу симметрии плотность тока на поверхности сферы направлена по нормали к ней и во всех точках имеет величину:

. (1)

По закону Ома в дифференциальной форме напряжённость поля равна:

. (2)

Теперь потенциал найдётся интегрированием:

,

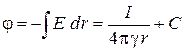причём, если принять, что 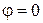при , то , и потенциал

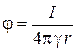. (3)

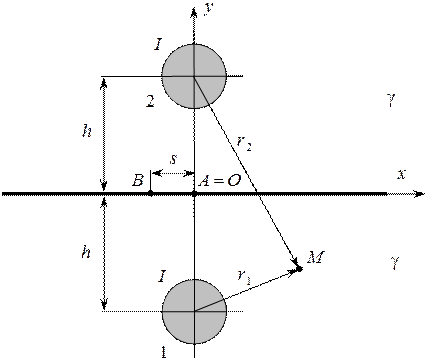
Рис. П2

Потенциал двух шаров в произвольной точке (см. рис. 2) найдём сложением:

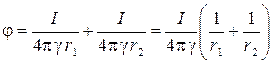. (4)

Опустим точку 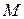на поверхность 1-го шара. При этом , ,

.

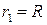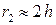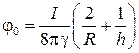Сопротивление шарового заземлителя:

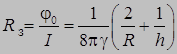. (5)

Теперь найдём шаговое напряжение 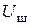между точкам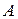и и 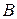. Для точки 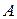: 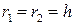; для точки 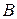: 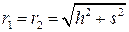. Потенциалы:

,

и шаговое напряжение:

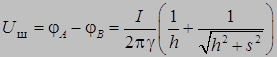. (6)

Предельный ток 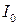, соответствующий предельному шаговому напряжению :

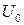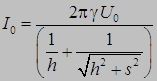. (7)

Формула (4) будет представлять формулу для нахождения потенциала в любой точке пространства, необходимую для построения картины эквипотенциальных линий во время компьютерного моделирования, если ввести систему координат 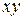(см. рис. 2) и в ней расписать расстояния , :

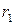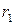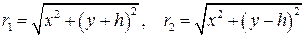. (6)

Тогда

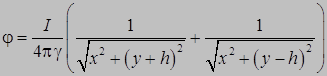. (7)

Формулы для составляющих 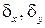плотности тока (составляющих 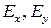напряжённости электрического поля) в любой точке внутри земли, необходимые для построения картины линий тока, получим из соотношений:

.

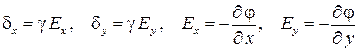Окончательно:

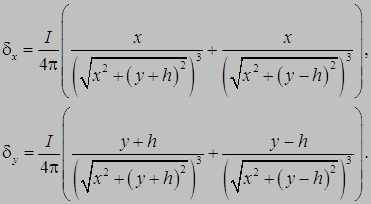. (8)