Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Саратов 2011

Саратовский государственный технический университет

Исследование РЕЗОНАНСА НАПРЯЖЕНИЙ В ПОСЛЕДОВАТЕЛЬНОМ rlc - КОНТУРЕ

Методические указания

к выполнению лабораторной работы

по курсу «Теоретические основы электротехники»

для студентов специальностей

200300, 200500 (направление 654100), 210300 (направление 652000),

210100 (направление 651900), 100400 (направление 650900), 180500 (направление 654500),

120200 (направление 651400), 120100 (направление 657800), 200700 (направление 654200)

Одобрено

редакционно-издательским отделом

Саратовского государственного технического университета

Саратов 2011

Цель работы: экспериментальное изучение линейной цепи синусоидального тока, состоящей из последовательно соединенных активного сопротивления, индуктивной катушки и конденсатора. Изучение основных закономерностей в такой цепи. Изучение резонанса напряжений.

Основные понятия

Существуют системы элементов, которые называются гармоническими осцилляторами, отличительной особенностью которых является возможность возникновения в них гармонических (синусоидальных) колебаний с некоторой определенной частотой ω ₀ при наличии некоторого запаса энергии. Эта частота называется собственной частотой системы. Примерами таких систем являются груз, подвешенный на пружине, или электрический контур, содержащий емкость и индуктивность.

Рассмотрим цепь, содержащую последовательно соединенные индуктивность, емкость и активное сопротивление (рис. 1). Запишем закон Ома для этой цепи:

,

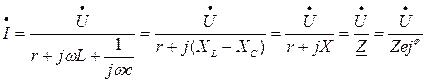или для действующих значений:

.

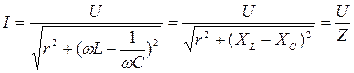В общем случае ток и напряжение в такой цепи не совпадает по фазе. Это видно из векторной диаграммы (рис. 2). Угол сдвига фаз 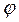между током 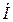и напряжением :

,

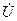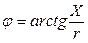где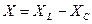

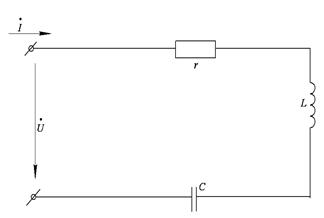
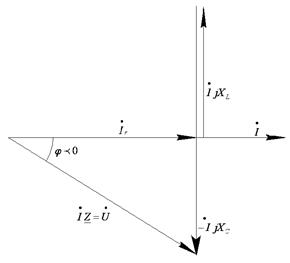
Рис.1 Рис.2

Резонанс напряжений - это явление, наступающее в электрической цепи синусоидального тока, содержащей последовательно соединенные активное сопротивление, индуктивную катушку и конденсатор, и заключающееся в том, что ток в цепи и приложенное ко всей цепи напряжение совпадают по фазе. Резонанс в последовательном RLC - контуре возникает при равенстве реактивных сопротивлений конденсатора и катушки индуктивности:

,

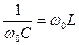откуда определяется резонансная частота контура .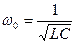

При резонансе напряжения на C и L могут существенно превышать входное напряжение. Если сравнивать резонанс в электрических цепях с резонансом в механике, то роль трения играет активное сопротивление r, причем при его увеличении добротность снижается. Полное сопротивление такой цепи в комплексной форме запишется в виде:

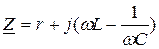
Условие резонанса можно добиться, изменяя С, L и 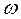. В данной работе мы рассматриваем резонанс, возникающий в ходе изменения частоты источника .

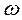Векторная диаграмма для случая резонанса дана на рис.3. Из нее мы имеем,

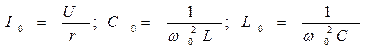
где 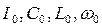- резонансные значения соответствующих величин.

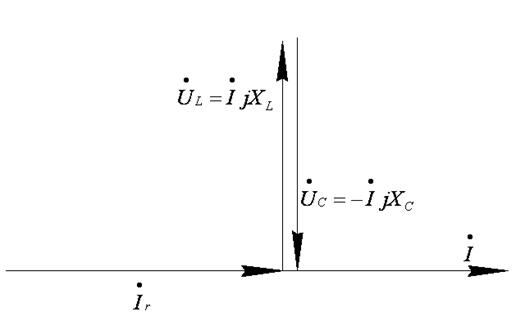
Рис.3

Зависимости тока и напряжения на индуктивности и емкости от частоты называются резонансными кривыми показанными на рис.4.

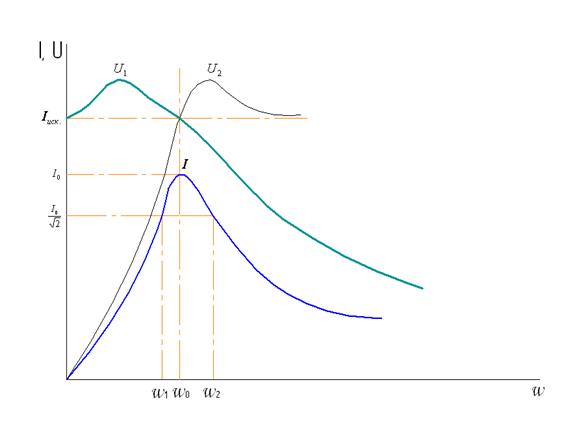
Рис.4

Полосу частот вблизи резонанса, на границе которой ток снижается в 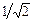раз по сравнению с резонансным значением, называют полосой пропускания резонансного контура. При резонансе ток в цепи I₀=E/R имеет максимальное значение. Отношение напряжения на реактивных элементах к входному напряжению называется добротностью контура, которая может быть определена также как отношение реактивного сопротивления конденсатора или катушки индуктивности к активному сопротивлению:

.

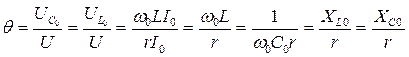Эта величина показывает, во сколько раз напряжение на реактивных сопротивлениях превышает входное напряжение в режиме резонанса.

Если частота входного напряжения 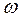< 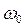,, то сопротивление конденсатора превышает сопротивление катушки индуктивности, а при 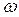> 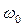, наоборот, сопротивление катушки превышает сопротивление конденсатора. В первом случае сопротивление всего контура носит активно-емкостной характер, а во втором - активно-индуктивный.

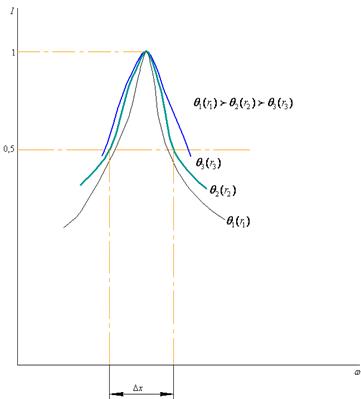
Рис.5

Добротность контура также можно определить при помощи характеристики 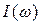по формуле:

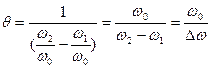
где 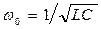- резонансная частота; 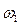и - значения граничных частот полосы пропускания 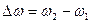, соответствующие двум равным токам 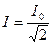при разных знаках угла сдвига фаз .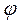