Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методика удлинения ряда наблюдений
|
|
Ряд непрерывных наблюдений имеет количество членов от 1 до n. Номер N. под которым в этот ряд можно поместить расход QВИУ. можно определить по эмпирической формуле Н.Н. Чегодаева
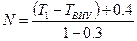. (5.12)
где ТВИУ – год наблюдения высокого исторического уровня;
Т1 – год наивысшего расхода из ряда непрерывных
наблюдений.
Удлиненный ряд наблюдений по номерам расходов будет выглядеть следующим образом:
1; 2; ……. n –1; n; n +1; …. N -1; N.
В этом ряду расходы располагаются в порядке возрастания. Расходы с порядковыми номерами от 1 до n соответствуют ряду непрерывных наблюдений, в диапазоне от n +1 до N -1 наблюдения отсутствуют. Считается, что в период отсутствия наблюдений средний расход по величине равен среднему расходу за период непрерывных наблюдений без учета наибольшего расхода в этом ряду. На основании этих предпосылок вычисляется:
– среднее арифметическое значение ряда Q¢ средн .;
– коэффициент вариации (изменчивочти) ряда С¢ V;
– коэффициент асимметрии ряда С¢ S.
по следующим формулам:
, (5.13)
где QN – расход при высоком историческом уровне (ВИУ);
N – номер ВИУ в удлиненном ряду;
n – номер наивысшего расхода в непрерывной части ряда,
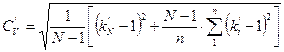, (5.14)
где
; (5.15)
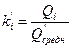; (5.16)
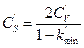; (5.17)
Расход заданной вероятности превышения определяется по формуле:
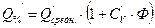(м3/сек). (5.18)
где Ф – табличный параметр (табл. 5.5).
Таблица 5.5.
Значения параметра Ф в зависимости от CS и вероятности превышения
| CS | Вероятность превышения паводка | ||||||||
| 1: 1000 | 1: 500 | 1: 300 | 1: 100 | 1: 50 | 1: 33 | 1: 25 | 1: 10 | 1: 5 | |
| Значения параметра Ф | |||||||||
| 0.0 | 3.1 | 2.9 | 2.7 | 2.3 | 2.0 | 1.9 | 1.8 | 1.3 | 0.8 |
| 0.1 | 3.3 | 3.0 | 2.8 | 2.4 | 2.1 | 1.9 | 1.8 | 1.3 | 0.8 |
| 0.2 | 3.4 | 3.1 | 2.9 | 2.5 | 2.1 | 1.9 | 1.8 | 1.3 | 0.8 |
| 0.3 | 3.5 | 3.2 | 3.0 | 2.6 | 2.2 | 1.9 | 1.8 | 1.3 | 0.8 |
| 0.4 | 3.7 | 3.3 | 3.1 | 2.6 | 2.2 | 2.0 | 1.8 | 1.3 | 0.8 |
| 0.5 | 3.8 | 3.5 | 3.3 | 2.7 | 2.3 | 2.0 | 1.9 | 1.3 | 0.8 |
| 0.6 | 4.0 | 3.6 | 3.3 | 2.8 | 2.3 | 2.1 | 1.9 | 1.3 | 0.8 |
| 0.7 | 4.1 | 3.7 | 3.4 | 2.8 | 2.4 | 2.1 | 1.9 | 1.3 | 0.8 |
| 0.8 | 4.2 | 3.8 | 3.5 | 2.9 | 2.4 | 2.1 | 2.0 | 1.3 | 0.8 |
| 0.9 | 4.3 | 3.9 | 3.7 | 3.0 | 2.4 | 2.1 | 2.0 | 1.3 | 0.8 |
| 1.0 | 4.5 | 4.1 | 3.7 | 3.0 | 2.5 | 2.2 | 2.0 | 1.3 | 0.8 |
| 1.1 | 4.7 | 4.2 | 3.8 | 3.1 | 2.5 | 2.2 | 2.0 | 1.3 | 0.7 |
| 1.2 | 4.8 | 4.3 | 3.9 | 3.1 | 2.6 | 2.2 | 2.1 | 1.3 | 0.7 |
| 1.3 | 5.0 | 4.4 | 4.0 | 3.2 | 2.6 | 2.3 | 2.1 | 1.3 | 0.7 |
| 1.4 | 5.1 | 4.6 | 4.1 | 3.3 | 2.7 | 2.3 | 2.1 | 1.3 | 0.7 |
| 1.5 | 5.2 | 4.7 | 4.2 | 3.3 | 2.7 | 2.3 | 2.1 | 1.3 | 0.7 |
| 1.6 | 5.4 | 4.8 | 4.3 | 3.4 | 2.8 | 2.4 | 2.1 | 1.3 | 0.7 |
| 1.7 | 5.5 | 4.9 | 4.4 | 3.4 | 2.8 | 2.4 | 2.2 | 1.3 | 0.7 |
| 1.8 | 5.7 | 5.0 | 4.5 | 3.5 | 2.8 | 2.4 | 2.2 | 1.3 | 0.6 |
| 1.9 | 5.8 | 5.1 | 4.5 | 3.5 | 2.8 | 2.4 | 2.2 | 1.3 | 0.6 |
| 2.0 | 5.9 | 5.2 | 4.6 | 3.6 | 2.9 | 2.5 | 2.2 | 1.3 | 0.6 |
| 2.1 | 6.0 | 5.3 | 4.8 | 3.6 | 2.9 | 2.5 | 2.2 | 1.3 | 0.6 |
| 2.2 | 6.2 | 5.4 | 4.9 | 3.7 | 2.9 | 2.5 | 2.2 | 1.3 | 0.6 |
| 2.3 | 6.4 | 5.5 | 4.9 | 3.7 | 2.9 | 2.5 | 2.2 | 1.3 | 0.6 |
| 2.4 | 6.5 | 5.7 | 5.0 | 3.8 | 3.0 | 2.5 | 2.2 | 1.2 | 0.5 |
| 2.5 | 6.6 | 5.8 | 5.0 | 3.8 | 3.0 | 2.5 | 2.2 | 1.2 | 0.5 |
| 2.6 | 6.7 | 5.8 | 5.1 | 3.9 | 3.0 | 2.5 | 2.2 | 1.2 | 0.5 |
| 2.7 | 6.9 | 5.9 | 5.2 | 3.9 | 3.0 | 2.5 | 2.2 | 1.2 | 0.5 |
| 2.8 | 7.0 | 6.0 | 5.3 | 3.9 | 3.0 | 2.5 | 2.2 | 1.2 | 0.5 |
| 2.9 | 7.1 | 6.1 | 5.4 | 4.0 | 3.1 | 2.5 | 2.2 | 1.2 | 0.5 |
| 3.0 | 7.2 | 6.3 | 5.4 | 4.0 | 3.1 | 2.5 | 2.2 | 1.2 | 0.4 |
| 3.2 | 7.5 | 6.5 | 5.5 | 4.1 | 3.1 | 2.5 | 2.3 | 1.1 | 0.4 |
| 3.5 | 7.9 | 6.8 | 5.8 | 4.2 | 3.2 | 2.5 | 2.3 | 1.1 | 0.3 |
|
|