
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
VI.3. Символьное представление чисел
|
|
В 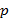 -ичной позиционной системе счисления для изображения чисел используются
-ичной позиционной системе счисления для изображения чисел используются 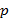 цифр и знаки " +" и " − ". Записи
цифр и знаки " +" и " − ". Записи
 ,
,
± 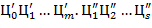 ,
,
± 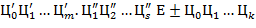 ,
,
где 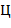 (с индексами и штрихами) −
(с индексами и штрихами) − 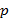 -ичные цифры, служат для изображения соответственно целого числа
-ичные цифры, служат для изображения соответственно целого числа
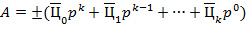
и вещественных чисел
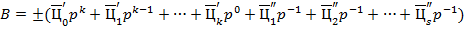
и
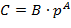 ,
,
где 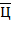 − числовое значение цифры
− числовое значение цифры 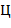 . Отметим, что любое вещественное число
. Отметим, что любое вещественное число 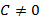 может быть представлено в виде
может быть представлено в виде 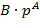 , где
, где 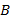 − вещественное число, называемое мантиссой, такое, что
− вещественное число, называемое мантиссой, такое, что 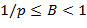 , а
, а 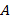 − целое, называемое порядком. Полезные сведения о различных способах записи чисел можно подчерпнуть, например, у Д. Кнута ([9], том 2, гл. 4).
− целое, называемое порядком. Полезные сведения о различных способах записи чисел можно подчерпнуть, например, у Д. Кнута ([9], том 2, гл. 4).
49. (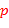 -ичные таблицы). Напечатать таблицы сложения и умножения чисел для
-ичные таблицы). Напечатать таблицы сложения и умножения чисел для 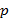 -ичной системы счисления,
-ичной системы счисления, 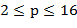 .
.
50. (Преобразования из одной формы в другую.)
а) Преобразовать целое число 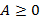 из внутренней формы представления в его символьное представление
из внутренней формы представления в его символьное представление 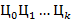 в
в 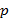 -ичной системе счисления.
-ичной системе счисления.
б) Преобразовать вещественное число 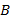
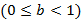 из внутренней формы представления в его символьное представление
из внутренней формы представления в его символьное представление 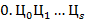 в
в 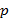 -ичной системе счисления. Здесь
-ичной системе счисления. Здесь 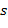 − заданное целое число, которое показывает, сколько цифр должно быть учтено в дробной части.
− заданное целое число, которое показывает, сколько цифр должно быть учтено в дробной части.
в) Преобразовать вещественное число 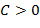 из внутренней формы представления в
из внутренней формы представления в 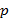 -ичной системе счисления вида
-ичной системе счисления вида 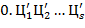
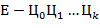 , где
, где 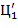 − значащая цифра, т.е.
− значащая цифра, т.е. 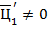 (или, что то же самое,
(или, что то же самое, 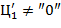 ).
).
г) Выполнить обратные преобразования.
Указания. а) значение цифры 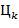 равно остатку от деления
равно остатку от деления 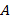 на
на 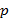 . Остальные цифры найти нетрудно, если учесть, что
. Остальные цифры найти нетрудно, если учесть, что 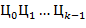 есть
есть 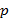 -ичное представление числа
-ичное представление числа 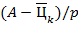 . б) Здесь значение
. б) Здесь значение 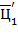 цифры
цифры 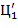 равно целой части числа
равно целой части числа 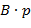 . Чтобы найти остальные цифры следует учесть, что
. Чтобы найти остальные цифры следует учесть, что 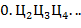 есть символьное представление числа
есть символьное представление числа 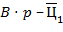 . в) Для получения тербуемого представления сначала необходимо найти вещественное число
. в) Для получения тербуемого представления сначала необходимо найти вещественное число 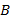 и целое
и целое 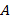 такие, что
такие, что 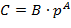 ,
, 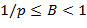 . Тогда
. Тогда 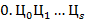 есть символьное представление числа
есть символьное представление числа 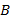 , а
, а  есть символьное представление числа
есть символьное представление числа 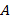 .
.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
51. (Операции над числами в символьном представлении.)
а) Сложить и перемножить два целых числа вида
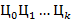
одинаковой длины.
б) Сложить и перемножить два вещественных числа вида
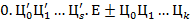 ,
,
представленных в символьном виде в 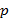 -ичной системе счисления. Рекомендация: операции выполнить, не переходя к внутреннему представлению чисел − в этом″ соль″ задания.
-ичной системе счисления. Рекомендация: операции выполнить, не переходя к внутреннему представлению чисел − в этом″ соль″ задания.
52. (Числа-палиндромы.) Палиндромы − это десятичное число, читаемое одинаково туда и обратно. Например, 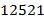 – палиндром. Возьмём любое число
– палиндром. Возьмём любое число 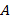 . Если это не палиндром, то реверсируем его цифры, т.е. запишем их в обратном порядке. В результате получим некоторое число
. Если это не палиндром, то реверсируем его цифры, т.е. запишем их в обратном порядке. В результате получим некоторое число 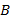 . Вычислим
. Вычислим
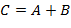 . Если
. Если 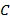 − не палиндром, то описанные действия повторяются до тех пор пока не получим палиндром. Проверить этот алгоритм для чисел
− не палиндром, то описанные действия повторяются до тех пор пока не получим палиндром. Проверить этот алгоритм для чисел 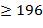 . (Замечание.
. (Замечание. 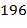 − первое число, для которого не известно, работает ли этот алгоритм. Указание. Здесь могут получаться большие числа. Поэтому их следует представить в символьном виде, используя для этой цели достаточно длинные массивы с компонентами – цифрами.)
− первое число, для которого не известно, работает ли этот алгоритм. Указание. Здесь могут получаться большие числа. Поэтому их следует представить в символьном виде, используя для этой цели достаточно длинные массивы с компонентами – цифрами.)
53. (Точное представление.) Напечатать точное десятичное представление несократимой, рациональной дроби 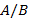 ,
, 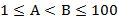 . Периодическая часть дроби должна быть отделена от непериодической части пробелом или отделена скобками. Образец печати:
. Периодическая часть дроби должна быть отделена от непериодической части пробелом или отделена скобками. Образец печати:
1 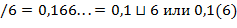
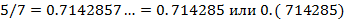
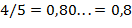
54. (Римские цифры.)
а) Записать заданное целое число римскими цифрами.
б) выполнить обратное преобразование.
Указание. Для записи чисел в римской нотации, которая, заметим, не является позиционной, используются цифры I (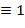 ), V (
), V (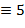 ), X (
), X (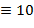 ), L (
), L (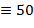 ), C (
), C (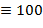 ), D
), D 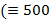 ), M (
), M (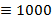 ). Считать, что все числа не превосходят
). Считать, что все числа не превосходят 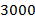 .
.
V.1.4. Задачи из раздела " Синтаксис и компиляция"
55. (Распознавание регулярных цепочек символов.)
а) Следующая синтаксическая диаграмма дает правило конструирования регулярного выражения из букв 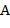 ,
, 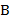 и
и 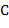 :
:
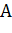
|

|
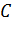
|
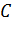
|
 BB
BB
|

Примерами регулярных выражений, полученных по этой диаграмме, являются: 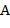 ,
, 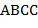 ,
, 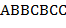 ,
, 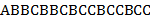 .
.
а) Установить, является ли заданная последовательность букв регулярным выражением указанного типа.
Указание. Разрешен только однократный просмотр исходной последовательности, т.е. слева направо, без возвратов.
б) решить задачу а), считая, что регулярное выражение задается одной из следующих диаграмм (на выбор):
Вставить рисунок на стр. 22
Вставить рисунок на стр. 22
Вставить рисунок на стр. 23
Вставить рисунок на стр. 23
56. (Распознавание некоторых синтаксических конструкций.)
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Используя синтаксические диаграммы, определим следующие конструкции:
Имя:
Целое:
integer
Описание имя:
, char
имя
множество [ ]
целое
,
список формальных параметров:
integer
(имя:)
, char
;
ВСТАВИТЬ РИСУНОК НА СТР. 23
для заданной последовательности символов установить, является ли она: а) именем, б) целым, в) описанием, г) множеством, д) списком формальных параметров.
57. (Правильная последовательность скобок.) Правильная последовательность скобок (сокращенно: ППС) - это конструкция, определяемая следующей диаграммой:
()
ППС
Вставить рисунок на стр. 24
Для заданной последовательности символов установить, являет ся ли она ППС.
Поясняющие примеры. Последовательности ″ ()(())″ и ″ (()())″ являются ППС, а ″ (()))(.)(″ и ″)()()()(″ не являются.
Указание. При просмотре последовательности слева направо необходимо контролировать, чтобы число просмотренных закрывающих скобок не превышало числа открывающих. К концу просмотра число закрывающих скобок должно сравняться с числом открывающих.
58. (Язык Дика 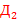 .) Слова языка
.) Слова языка 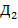 определяются следующей синтаксической программой:
определяются следующей синтаксической программой:
(слово)
[ слово ]
Вставить рисунок на стр. 24
Для заданной последовательности символов установить, является ли она. словом языка 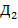 .
.
Поясняющие примеры. Последовательность скобок ″ [(([()]))]()″ является словом языка 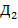 а последовательность ″ [(]]″ нe является.
а последовательность ″ [(]]″ нe является.
Указание. От " правильной последовательности скобок " предыдущей задачи " слова" этой задачи отличаются лишь наличием двух сортов скобок. Для контроля правильности закрытия скобок удобно использовать специальный массив-стек. При просмотре исходного текста в стек помещаются только открывающие скобки; если встречается закрывающая скобка, то соответствующая открывающая исключается из стека. Подчеркиваем, что закрыться может только последняя (!) из незакрытых скобок, причем если только она парна текущей закрывающей скобке. Поэтому стек либо заполняется слева, направо, либо освобождается справа налево. Замечание. Можно устранить использование стека, применяя технику, известную в математической логике под названием " гёделизация". Вместо стека заведем целочисленную переменную 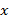 с начальным значением
с начальным значением 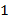 . Запоминанию в стеке символа " (" (или " [") соответствует преобразование
. Запоминанию в стеке символа " (" (или " [") соответствует преобразование 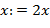 (или
(или 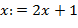 ). Исключению последней скобки из стека соответствует преобразование
). Исключению последней скобки из стека соответствует преобразование 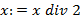 . Последняя, скобка в стеке суть " (", когда
. Последняя, скобка в стеке суть " (", когда 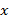 четно, и " [", когда
четно, и " [", когда 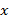 нечетно. Почему текущее значение
нечетно. Почему текущее значение 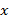 всегда будет однозначно кодировать текущее состояние стека? Как обобщить это кодирование на случай
всегда будет однозначно кодировать текущее состояние стека? Как обобщить это кодирование на случай 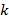 сортов скобок?
сортов скобок?
59. (Использование стека.) Текст 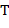 , составленный из букв "
, составленный из букв " 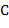 " и "
" и " 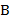 ", называется допустимым, если 1) число вхождений буквы "
", называется допустимым, если 1) число вхождений буквы " 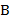 " не превышает числа вхождений буквы "
" не превышает числа вхождений буквы " 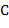 " при чтении слева направо и 2) число букв "
" при чтении слева направо и 2) число букв " 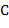 " и " B " в тексте одинаково.
" и " B " в тексте одинаково.
а) Установить, является ли заданный текст допустимым.
б) Пусть 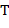
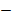 заданный допустимый текст длины
заданный допустимый текст длины 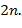 Преобразовать входной текст длины n (символов) в выходной текст, выполняя следующие действия. Пусть α и β − очередные символы соответственно текста
Преобразовать входной текст длины n (символов) в выходной текст, выполняя следующие действия. Пусть α и β − очередные символы соответственно текста 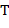 и входного текста (при чтении текстов слева направо). Тогда, если
и входного текста (при чтении текстов слева направо). Тогда, если  , то β помещается в стек; Если же
, то β помещается в стек; Если же 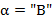 , то. символ, записанный в вершине стека, перемещается в выходной текст.
, то. символ, записанный в вершине стека, перемещается в выходной текст.
Пояснения. 1) Стек − это линейный список, в котором все включения и исключения осуществляются на правом конце, называемом вершиной стека. Таким образом, стек либо заполняется слева направо, либо освобождается справа налево. Для моделирования стека здесь рекомендуется использовать массив.
2) " 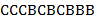 " − пример допустимого текста
" − пример допустимого текста 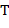 . Применяя его к входному тексту "
. Применяя его к входному тексту " 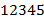 ", получаем выходной текст "
", получаем выходной текст " 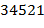 ".
".
60. (Использование дека с ограниченным выходом.) Текст, составленный из букв 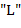 ,
, 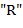 и
и 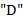 , называется допустимым, если 1) число вхождений буквы
, называется допустимым, если 1) число вхождений буквы 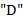 не превышает суммарного числа вхождений букв
не превышает суммарного числа вхождений букв 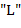 и
и 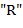 при чтении слева направо; 2) общее число вхождений в текст буквы
при чтении слева направо; 2) общее число вхождений в текст буквы 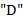 равно суммарному числу вхождений в текст букв
равно суммарному числу вхождений в текст букв 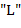 и
и 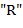 ;
;
(3) если при чтении текста слева направо в некоторый момент времени число вхождений буквы 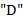 равно
равно 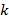 , а число вхождений букв
, а число вхождений букв 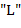 и
и 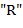 также равно
также равно 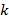 , то
, то 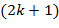 -ый символ текста есть
-ый символ текста есть 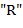 , 4) сочетание букв
, 4) сочетание букв 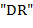 не допустимо, если это не противоречит 3).
не допустимо, если это не противоречит 3).
а) Установить, является ли заданный текст допустимым.
б) Пусть 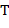 − заданный допустимый текст длины
− заданный допустимый текст длины 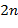 . Преобразовать входной текст длины
. Преобразовать входной текст длины 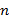 (символов) в выходной текст, выполняя следующие действия. Пусть
(символов) в выходной текст, выполняя следующие действия. Пусть 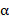 и β − очередные символы соответственно из текста
и β − очередные символы соответственно из текста 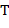 и входного текста (при чтении текстов слева направо). Тогда, если
и входного текста (при чтении текстов слева направо). Тогда, если 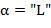 или
или 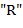 , тоβ помещается в дек соответственно в левый (
, тоβ помещается в дек соответственно в левый (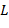 ) или правый конец (
) или правый конец (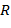 ), если же
), если же 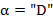 , то символ, записанный в деке на левом конце, исключается из дека и перемещается в выходной текст.
, то символ, записанный в деке на левом конце, исключается из дека и перемещается в выходной текст.
Пояснения. 1) Дек − это линейный список, в котором все включения и исключения (и всякий доступ) возможны на обоих концах списка. Для моделирования дека здесь рекомендуется использовать массив. 2) 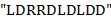 пример допустимого текста. Применяя его к входному тексту
пример допустимого текста. Применяя его к входному тексту 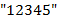 , получаем выходной текст
, получаем выходной текст 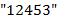 .
.
61. (Выделение подтерма.) Термы образуются из переменных и функциональных символов. Функциональные символы − это имена функций; каждый функциональный символ имеет размерность (или местность, или арность) − число аргументов функции. Общее определение терма таково:
1) переменная есть терм;
2) если 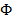 − функциональный символ размерности
− функциональный символ размерности 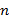 , а
, а 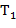 ,
, 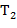 ,...,
,..., 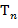 − термы, то
− термы, то 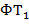 ,
, 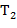 ,...,
,..., 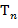 − тоже терм, причем его (собственными) подтермами называются термы
− тоже терм, причем его (собственными) подтермами называются термы 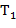 ,
, 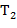 ,...,
,..., 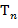 и их подтермы. Рассмотрим частный случай. Пусть
и их подтермы. Рассмотрим частный случай. Пусть 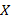 ,
, 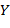 ,
, 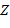 − переменные, а
− переменные, а 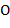 ,
, 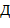 ,
, 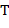 − функциональные символы соответственно размерности
− функциональные символы соответственно размерности 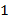 ,
,  ,
, 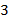 (
(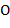 − один,
− один, 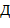 − два,
− два, 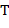 − три). Тогда термы − это слова, определяемые синтаксической диаграммой:
− три). Тогда термы − это слова, определяемые синтаксической диаграммой:
X
Y
Z
О
Д
Т терм терм терм
Например, 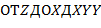 − терм, который для наглядности часто изображают в виде
− терм, который для наглядности часто изображают в виде 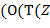 ,
, 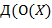 ,
, 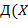 ,
, 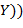 ,
, 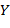 ). Одним из его подтермов является терм
). Одним из его подтермов является терм 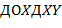 .
.
В заданной последовательности символов, являющейся термом, выделить первый подтерм, начинающийся с функционального символа 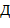 , т.е. вычислить номера позиций начала и конца этого подтерма.
, т.е. вычислить номера позиций начала и конца этого подтерма.
Указание. Чтобы вычислить номер конечной позиции подтерма, потребуется в процессе просмотра подтерма слева направо считать количество еще незаполненных аргументных мест.
Подтерм, начинающийся с функционального символа 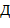 , имеет
, имеет 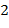 аргументных места. Переменная заполняет в точности одно аргументное место. Функциональный символ размерности
аргументных места. Переменная заполняет в точности одно аргументное место. Функциональный символ размерности 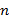 отменяет необходимость заполнить одно аргументное место, но вызывает необходимость заполнить
отменяет необходимость заполнить одно аргументное место, но вызывает необходимость заполнить 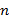 аргументных мест. Когда число аргументных мест, требующих заполнения, станет равным нулю, тогда подтерм и закончится.
аргументных мест. Когда число аргументных мест, требующих заполнения, станет равным нулю, тогда подтерм и закончится.
62. (Синтаксический анализ простых арифметических выражений.) Арифметические выражения в скобочной (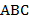 ) и бесскобочной (
) и бесскобочной (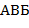 ) нотациях определяются следующим образом:
) нотациях определяются следующим образом:

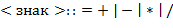
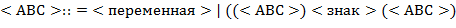
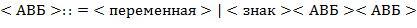
Пример записи одного и того же выражения в скобочной и бесскобочной нотациях: 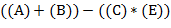 и
и 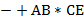 .
.
Написать программы для проверки правильности запись арифметических выражений в виде 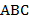 и
и 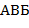 .
.
Указание. В строке символов 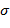 , являющейся записью арифметического выражения, заменим каждую букву на цифру " 0" и каждый знак на цифру "
, являющейся записью арифметического выражения, заменим каждую букву на цифру " 0" и каждый знак на цифру " 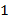 ". В результате получим строку
". В результате получим строку 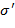 . Справедливо утверждение:
. Справедливо утверждение: 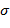 есть
есть 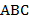 (соответственно
(соответственно 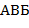 ) тогда и только тогда, когда
) тогда и только тогда, когда 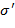 может быть превращена в цифру
может быть превращена в цифру 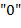 заменами ее подстрок
заменами ее подстрок 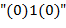 (соответственно
(соответственно 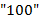 ) на
) на 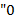 ".
".
Остальное − дело техники. Впрочем, отметим, что синтаксис 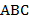 и
и 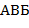 рекурсивен. Поэтому написание рекурсивных процедур − здесь также подходящий способ решения поставленной задачи. Можно также использовать стек.
рекурсивен. Поэтому написание рекурсивных процедур − здесь также подходящий способ решения поставленной задачи. Можно также использовать стек.
63. (Перевод в прямую польскую запись. Обратный перевод.)
а) Преобразовать арифметическое выражение, представленное в виде 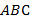 , в арифметическое выражение представленное в виде
, в арифметическое выражение представленное в виде 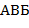 . (Синтаксис
. (Синтаксис 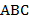 и
и 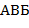 дан в задаче 58. Запись выражения в виде
дан в задаче 58. Запись выражения в виде 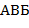 называется прямой польской записью.)
называется прямой польской записью.)
б) Выполнить обратное преобразование (переход от 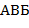 к
к 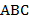 ).
).
Указания. Предположим, что строка символов 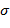 представляет
представляет 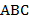 или
или 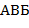 .
.
а) Алгоритм перевода 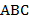 в
в 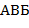 заключается в следующем: в б отыскивается часть строки
заключается в следующем: в б отыскивается часть строки 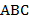 вида
вида 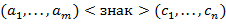 , где
, где 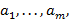
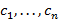 − буквы или знаки (но не скобки), эта часть заменяется на
− буквы или знаки (но не скобки), эта часть заменяется на 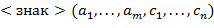 . Это действие повторяется до тех пор, пока в строке не исчезнут все скобки,
. Это действие повторяется до тех пор, пока в строке не исчезнут все скобки,
б) Перевод 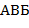 в
в 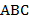 осуществляется так: сначала все переменные (т.е.буквы) заключаются в круглые скобки на каждом последующем шаге отыскивается подстрока вида
осуществляется так: сначала все переменные (т.е.буквы) заключаются в круглые скобки на каждом последующем шаге отыскивается подстрока вида 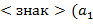 ,...,
,..., 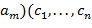 ) такая, чтокак среди
) такая, чтокак среди 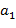 ,...,
,..., 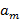 , так и среди
, так и среди 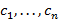 имеется одинаковое число открывающих и закрывающих скобок; она заменяется на подстроку
имеется одинаковое число открывающих и закрывающих скобок; она заменяется на подстроку 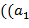 ,...,
,..., 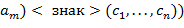 .Это повторяется до тех пор, пока первый символ исходной строки не превратится в открывающую скобку. После этого первая и последняя скобки удаляются. Другой алгоритм основан на использовании стека.
.Это повторяется до тех пор, пока первый символ исходной строки не превратится в открывающую скобку. После этого первая и последняя скобки удаляются. Другой алгоритм основан на использовании стека.
64. (Обработка арифметических выражений. Перевод в польскую запись и вычисление значения.) Здесь рассматриваются арифметические выражения, составленные из переменных, знаков операций и круглых скобок. Для обозначения переменных используются одиночные буквы. В качестве знаков операций используются  ,
, 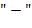 ,
, 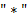 ,
,  и
и 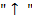 . Это − бинарные операции: сложение, вычитание, умножение, деление и возведение в степень. Операции имеют следующие приоритеты (отражающие старшинство операций):
. Это − бинарные операции: сложение, вычитание, умножение, деление и возведение в степень. Операции имеют следующие приоритеты (отражающие старшинство операций):
| операция | + − | ∗ ∕ | 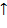
|
| приоритет |
В отличие от задачи 63, где рассматриваются выражения в полной скобочной записи, здесь некоторые скобки могут быть опущены. Так, вместо 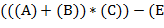 ) можно писать
) можно писать 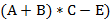 . В отличие от обычной инфиксной записи арифметических выражений, когда знаки операций помещаются между операндами, в суффиксной записи (другие названия: постфиксная, обратная польская запись) знаки операций помещаются после своих операндов. (Например,
. В отличие от обычной инфиксной записи арифметических выражений, когда знаки операций помещаются между операндами, в суффиксной записи (другие названия: постфиксная, обратная польская запись) знаки операций помещаются после своих операндов. (Например, 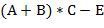 и
и 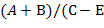 ) записываются в виде
) записываются в виде 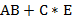 и
и 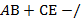 .)
.)
а) Преобразовать инфиксную запись арифметического выражения в суффиксную.
б) Каждой переменной (букве) арифметического выражения в суффиксной записи сопоставлено некоторое числовое значение. Вычислить значение выражения при обычной интерпретации арифметических операций.
Указания. а) Переход от инфиксной записи к суффиксной может быть осуществлен за один последовательный просмотр. Алгоритм преобразования основан на использовании стека − памяти, действующей по принципу " последним пришел – первым ушел":
1) из входной строки, являющейся записью исходного алгебраического выражения, извлекается очередной символ 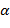 .
.
2) Если 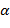 − открывающая скобка, то
− открывающая скобка, то 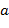 заносится в стек с приоритетом
заносится в стек с приоритетом 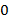 .
.
3) Если 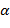 − буква, то
− буква, то 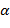 помещается в выходную строку.
помещается в выходную строку.
4) Если 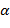 − операция и стек пуст, то
− операция и стек пуст, то 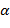 заносится в стек. Если стек не пуст, то приоритет
заносится в стек. Если стек не пуст, то приоритет 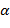 сравнивается с приоритетом символа
сравнивается с приоритетом символа 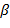 , находящегося на вершине стека. Если приоритет
, находящегося на вершине стека. Если приоритет 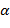 больше, то
больше, то 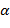 заносится в стек; в противном случае операция
заносится в стек; в противном случае операция 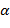 переносится с вершины стека в выходную строку и снова повторяется шаг 4) для новой вершины стека и т.д.
переносится с вершины стека в выходную строку и снова повторяется шаг 4) для новой вершины стека и т.д.
5) Если 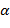 − закрывающая скобка, то операции из стека последовательно переносятся в выходную строку до тех пор, пока на вершине стека не окажется открывающая скобка; эта скобка уничтожается.
− закрывающая скобка, то операции из стека последовательно переносятся в выходную строку до тех пор, пока на вершине стека не окажется открывающая скобка; эта скобка уничтожается.
6) Если просмотр выходной строки еще не закончен, то переходим на шаг 1); в противном случае из стека последовательно переносятся все оставшиеся операции.
б) Вычисление значения выражения, представленного в суффиксной записи, также основано на использовании стека и может быть осуществлено за один последовательный просмотр:
1) Если очередной символ выражения есть буква, то сопоставляемое ей числовое значение заносится в стек.
2) Если очередной символ выражения есть знак операции 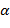 , то из стека извлекаются два числовых значения. Пусть эти значения суть
, то из стека извлекаются два числовых значения. Пусть эти значения суть 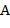 и
и 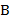 , причем
, причем 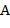 извлечено первым. Над ними выполняется соответствующая операция и значение
извлечено первым. Над ними выполняется соответствующая операция и значение 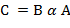 заносится в стек.
заносится в стек.
В результате такого просмотра в стеке останется только одно значение. Это и есть искомое значение выражения.
VI.5. Дополнительные задачи (трудные)
65. (Алгебра блоков.) Последовательность, составленную из литер 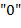 и
и 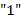 , будем называть блоком. Выражения над блоками в скобочной (
, будем называть блоком. Выражения над блоками в скобочной (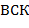 ), инфиксной (
), инфиксной (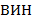 ) и префиксной (
) и префиксной (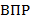 ) нотациях определяются так:
) нотациях определяются так:
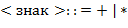
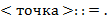
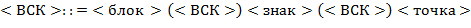
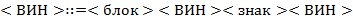
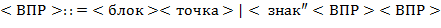
а) Выполнить преобразования 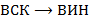 ,
, 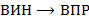 ,
, 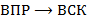 .
.
(Запись 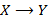 означает преобразование выражения вида
означает преобразование выражения вида 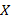 в выражение вида
в выражение вида 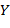 .)
.)
б) Вычислить блок, являющийся значением выражения вида 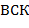 , при следующей трактовке операций блоками:
, при следующей трактовке операций блоками:
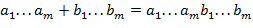
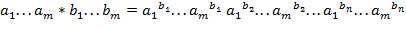
где 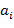 ,
, 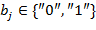 ,
, 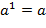 ,
, 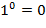 ,
,  .
.
Поясняющий пример:
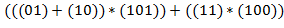
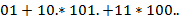
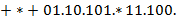
− записи одного и того же выражения соответственно в виде 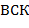 ,
, 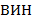 ,
, 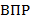 . Значение первого из них есть блок
. Значение первого из них есть блок 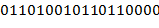 .
.
66. (Аналитическое, или символьное дифференцирование.) Синтаксис конструкции 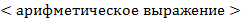 (обозначаемо ниже для краткости через
(обозначаемо ниже для краткости через 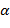 ,
, 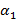 ,
, 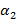 ,...) определен так:
,...) определен так:
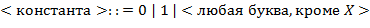
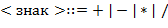
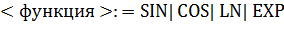
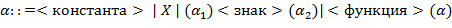
Пример конструкции 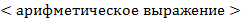 :
:
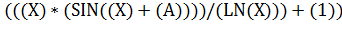
(это эквивалент выражения 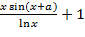 в обычной записи).
в обычной записи).
Найти 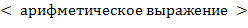 , являющееся
, являющееся 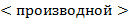 от заданного
от заданного 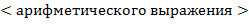 , используя следующие правила конструирования
, используя следующие правила конструирования 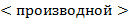 (обозначаемой через
(обозначаемой через 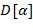 , если
, если 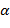 − соответствующее
− соответствующее 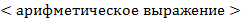 )
)
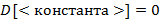
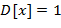

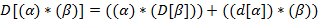
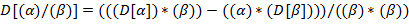
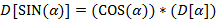
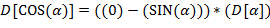
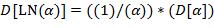
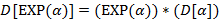
Указание. Правила (l) − (9) рекурсивны: в определении 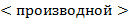 используется сама
используется сама 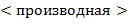 . Здесь можно использовать стек или описать рекурсивную процедуру.
. Здесь можно использовать стек или описать рекурсивную процедуру.
67. (Печать с выравниванием.) Входной текст представляет собой последовательность слов, разделенных пробелами, запятыми и точками. Напечатать его в соответствии со следующими требованиями:
ТРЕБОВАНИЯ К ПЕЧАТИ. СТРОКИ ДОЛЖНЫ БЫТЬ ОДНОЙ И ТОЙ ЖЕ
НАПЕРЁД ЗАДАННОЙ ДЛИНЫ. ПРИ ВВОДЕ ТЕКСТА ЛИШНИЕ ПРОБЕЛЫ
УДАЛЯЮТСЯ, А ЗНАКИ ПУНКТУАЦИИ ПОМЕЩАЮТСЯ НЕПОСРЕДСТВЕННО ЗА
ПРЕДМЕСТЗУЩИИИ БУКВАМИ. СЛОВА ПЕРЕНОСИТЬ НЕЛЬЗЯ. ПОСЛЕДНИЙ
СИМВОЛ В КАЖДОЙ СТРОКЕ НЕ ДОЛЖЕН БЫТЬ ПРОБЕЛОМ: ПОЭТОМУ ПРИ
ПЕЧАТИ МЕЖДУ СЛОВАМИ ВСТАВЛЯЮТСЯ ДОПОЛНИТЕЛЬНЫЕ ПРОВБЛЫ, НО
ТАК, ЧТОБЫ ПРОМЕЖУТКИ МЕЖДУ СЛОВАМИ БЫЛИ ПРИМЕРНО
ОДИНАКОВЫМИ. ПОСЛЕДНЯЯ СТРОКА НЕ ВЫРАВНИВАЕТСЯ.
68. (Составление подстрочника. − Примитивный перевод с английского на русский.) Предположим, что задан англо-русский словарь, образованный парами 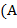 ,
, 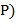 , где
, где 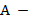 английское слово, а
английское слово, а 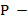 его русский перевод. Входной текст образован английскими словами. В качестве разделителей слов, предложений и их частей используются пробелы, точки и запятые.Преобразовать входной текст в выходной, заменяя каждое вхождение английского слова на его русский перевод. Лишние пробелы между словами убрать, а знаки пунктуации сохранить Если английское слово, встречающееся в тексте, отсутствует в словаре. то в выходной текст это слово помещается без перевода. Указания. В качестве структур данных для хранения англо-русского словаря использовать массив и файл записей вида
его русский перевод. Входной текст образован английскими словами. В качестве разделителей слов, предложений и их частей используются пробелы, точки и запятые.Преобразовать входной текст в выходной, заменяя каждое вхождение английского слова на его русский перевод. Лишние пробелы между словами убрать, а знаки пунктуации сохранить Если английское слово, встречающееся в тексте, отсутствует в словаре. то в выходной текст это слово помещается без перевода. Указания. В качестве структур данных для хранения англо-русского словаря использовать массив и файл записей вида 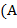 ,
, 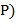 . При этом в массиве (″ быстрая память″) хранятся наиболее употребительные английские слова с их русскими эквивалентами, а в файле (внешний последовательный файл) записаны слова, относительно редко встречающиеся в текстах. Слопарь общеупотребительных слов желательно предварительно отсортировать, т.е. расположить английские слова по алфавиту − это позволит ускорить поиск нужных слов в словаре (применяя, пример, метод двоичного поиска вместо линейного поиска).
. При этом в массиве (″ быстрая память″) хранятся наиболее употребительные английские слова с их русскими эквивалентами, а в файле (внешний последовательный файл) записаны слова, относительно редко встречающиеся в текстах. Слопарь общеупотребительных слов желательно предварительно отсортировать, т.е. расположить английские слова по алфавиту − это позволит ускорить поиск нужных слов в словаре (применяя, пример, метод двоичного поиска вместо линейного поиска).
69. (Поиск анаграмм.) Анаграммой слова называется другое слово, полученное перестановкой букв. В заданном словаре русских слов найти все группы слов, являющиеся анаграммами друг друга. Печатать только те группы, которые состоят из двух или более слов.
70. (Головоломка по отгадыванию слов.) Даны список слов и таблица, составленная из букв. Напечатать каждое слово из списка, которое присутствует в таблице, если читать по горизонталям и диагоналям в любом направлении. Для заданного направления каждый из элементов таблицы может быть использован в качестве начального не более чем для одного слова из списка.
Пример. Пусть даны список слов (слева) и таблица (справа):
М О С К В А Ь А В О Т С О Р
К Л И Н Н Н М О С К В А К
Р О С Т О В А Е О С Л Н О Н
К А З А Н Ь З Ж Р М И Е Р Л
К У Р С К А У Б А Н И Р Д
М У Р О М К А Л У Г А Л О
К А Л У Г А
О Р Е Л
Тогда получаем решение:
Р О С Т О В 1, 8 В Л Е В О
М О С К В А 2, 2 В П Р А В О
К Л И Н 2, 5 В Н И З
К А З А Н Ь 6, 1 В В Е Р Х
К У Р С К 6, 1 В В Е Р Х – В П Р А В О
К А Л У Г А 6, 1 В П Р А В О
О Р Е Л 6, 8 В В Е Р Х – В Л Е В О
71. (Проверка решения кроссворда.) Рисунок кроссворда задан целочисленной матрицей. Неотрицательные числа обозначают белые клетки кроссворда а отрицательные − чёрные. Кроме того, положительные числа используются, как обычно, для нумерации клеток, начиная с которых вписываются соответствующие слова по горизонтали и вертикали. Имеется также два списка 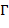 (горизонталь) и
(горизонталь) и 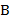 (вертикаль) слов, снабженных номерами.
(вертикаль) слов, снабженных номерами.
Установить, являются ли списки 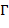 и
и 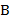 решением кроссворда.
решением кроссворда.
Пояснение. Произвольное слово 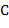 принадлежит
принадлежит 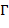 (соответственно,
(соответственно, 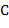 принадлежит
принадлежит 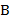 ), снабженное номером
), снабженное номером 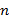 , должно быть вписанно в диаграмму кроссворда по горизонтали, начиная с клетки с тем же номером. Последовательности
, должно быть вписанно в диаграмму кроссворда по горизонтали, начиная с клетки с тем же номером. Последовательности 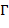 и
и 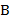 определяют решение кроссворда, если после его заполнения:
определяют решение кроссворда, если после его заполнения:
1) не останется белых клеток,
2) разные буквы не накладываются друг на друга,
3) ни одна из букв не вписана в чёрную клетку.
72. (Декомпозиция кроссворда.) Операция декомпозиции заполненного кроссворда заключается в следующем:
1) клетки кроссворда нумеруются так, как это принято для кроссвордов,
2) составляются списки пронумерованных слов по горизонтали и вертикали,
3) буквы в кроссворде заменяются пробелами.
Осуществить декомпозицию кроссворда.
73. (Рисунок кроссворда.) Рисунок кроссворда можно задать матрицей из 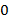 и
и 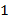 . При этом
. При этом 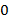 означает белый квадрат, а
означает белый квадрат, а 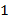 − черный. Для заданной матрицы напечатать рисунок кроссворда с нумерацией квадратов для слов " по горизонтали" и " по вертикали". Черные квадраты, примыкающие к границе убрать. Задание поясняет рис.1, иллюстрирующий переход от матрицы к соответствующему рисунку кроссворда.
− черный. Для заданной матрицы напечатать рисунок кроссворда с нумерацией квадратов для слов " по горизонтали" и " по вертикали". Черные квадраты, примыкающие к границе убрать. Задание поясняет рис.1, иллюстрирующий переход от матрицы к соответствующему рисунку кроссворда.
| ⟹ | |||||||||||||||
Рис.1 (к задаче 73)
74. (Развитие темы задач 1 и 10.) Найти наименьшее множество символов 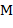 , при котором заданный текст
, при котором заданный текст 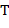 является
является 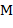 -перевертышем.
-перевертышем.
Замечание. Решение задачи заведомо существует. Если 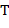 − палиндром, то
− палиндром, то 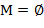 − пустое множество. Не исключено, что выбор
− пустое множество. Не исключено, что выбор 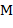 не однозначен. Так, текст-слово
не однозначен. Так, текст-слово 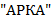 является
является 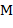 -перевертышем для
-перевертышем для 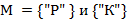 .
.
Указание. Быть может, при построении 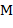 будет полезно учесть следующий факт. Предположим, что буква
будет полезно учесть следующий факт. Предположим, что буква 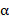 входит в текст
входит в текст 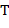 , но
, но 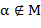 . Кроме того, пусть
. Кроме того, пусть 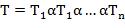 , где
, где 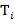 − фрагменты текста
− фрагменты текста 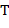 , не содержащие буквы
, не содержащие буквы 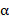 , а
, а 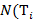 ,
, 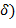 − число вхождений буквы
− число вхождений буквы 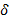 в фрагмент
в фрагмент 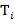 . Тогда, если
. Тогда, если 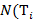 ,
, 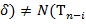 ,
, 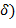 для некоторого
для некоторого 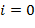 ,
,  ,
,  , то заведомо
, то заведомо 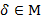 .
.
75. (Слова и кривые дракона.) Слово дракона 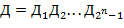 порядка
порядка 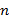 определяется так: значения букв
определяется так: значения букв 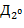 ,
, 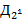 ,
, 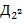 ,...,
,..., 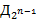 выбираются произвольно из алфавита
выбираются произвольно из алфавита 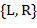 ; Если
; Если 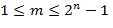 и
и 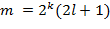 , где
, где 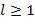 , то полагаем
, то полагаем

где 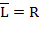 и
и 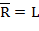 . (Нетрудно заметить, что имеется
. (Нетрудно заметить, что имеется 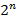 различных слов дракона порядка
различных слов дракона порядка 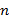 .) Два слова дракона
.) Два слова дракона 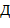 и
и 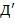 порядка
порядка 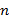 называют подобными, если после вычеркивания
называют подобными, если после вычеркивания
средней буквы эти слова либо совпадают, либо одно получается из другого заменой 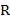 на
на 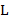 и
и 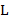 на
на 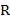 . Каждому слову дракона
. Каждому слову дракона 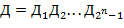 соответствует ломаная дракона. Она может быть начерчена так. Проведем отрезок
соответствует ломаная дракона. Она может быть начерчена так. Проведем отрезок 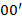 (Все отрезки имеют здесь одну и ту же длину.) Далее, если
(Все отрезки имеют здесь одну и ту же длину.) Далее, если 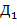 равно
равно 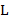 , то из точки
, то из точки 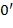 проведем влево (перпендикулярно к
проведем влево (перпендикулярно к 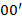 ) отрезок
) отрезок 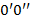 ; если же
; если же 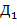 равно
равно 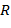 , то соответствующий отрезок проведем вправо. Аналогично построим отрезок
, то соответствующий отрезок проведем вправо. Аналогично построим отрезок 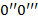 , соответствующий букв
, соответствующий букв 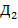 и т.д. На рис. 2 изображена ломаная дракона, соответствующая слову дракона.порядка
и т.д. На рис. 2 изображена ломаная дракона, соответствующая слову дракона.порядка 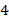 . Изломы отрезков закруглены для наглядности. О словах и ломаных дракона рассказывается, например, в статье [4].
. Изломы отрезков закруглены для наглядности. О словах и ломаных дракона рассказывается, например, в статье [4].
а) Напечатать все слова дракона порядка 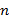 .
.
| R | L | |||||||
| R | R | L | R | |||||
| R | R | 0''' | L | 0'' | ||||
| L | L | |||||||
| R | 0' | |||||||
| R | L | |||||||
| R |
Рис.2 (к задаче 75). Ломаная дракона для слова 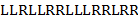
б) Множество всех слов дракона порядка 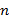 разбивается на классы попарно подобных слов..Напечатать по одному слову из каждого класса.
разбивается на классы попарно подобных слов..Напечатать по одному слову из каждого класса.
в) Для заданного слова дракона напечатать рисунок соответствующей ломаной дракона. (На рис. 2 элементы рисунка, подлежащие печати, показаны жирно.)
76. (Скатерть С. Улама, или картинки из простых чисел.) Напечатать картинку, которая получается следующим образом. В клетках поля размером 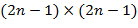 , где
, где 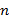 − заданное натуральное число, располагаются по спирали натуральные числа, начиная с заданного числа
− заданное натуральное число, располагаются по спирали натуральные числа, начиная с заданного числа 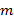 , которое помещается в центральную клетку. Затем простые числа заменяют символом
, которое помещается в центральную клетку. Затем простые числа заменяют символом 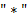 , а составные символом
, а составные символом  ⊔ " (пробел).
⊔ " (пробел).
Пример. При 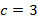 и
и 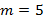 получаем
получаем
| A/B | |||||||||||
| ∗ | ∗ | ||||||||||
| ∗ | |||||||||||
|
|
