
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Задача о назначениях
|
|
Рассмотрим ситуацию, когда требуется распределить m работ (или исполнителей) по n станкам. Работа i (i=1,..., m), выполняемая на станке j (j=1,..., n), связана с затратами  . Задача состоит в таком распределении работ по станкам (одна работа выполняется на одном станке), которое соответствует минимизации суммарных затрат.
. Задача состоит в таком распределении работ по станкам (одна работа выполняется на одном станке), которое соответствует минимизации суммарных затрат.
Эту задачу можно рассматривать как частный случай транспортной задачи. Здесь работы представляют «исходные пункты», а станки – «пункты назначения». Предложение в каждом исходном пункте равно 1, т.е.  = 1 для всех i. Аналогично спрос в каждом пункте назначения равен 1, т.е. bj =1 для всех j. Стоимость «перевозки» (прикрепления) работы i к станку j равна cij. Если какую-либо работу нельзя выполнять на некотором станке, то соответствующая стоимость cij берется равной очень большому числу. Матрица стоимостей C определяется следующим образом:
= 1 для всех i. Аналогично спрос в каждом пункте назначения равен 1, т.е. bj =1 для всех j. Стоимость «перевозки» (прикрепления) работы i к станку j равна cij. Если какую-либо работу нельзя выполнять на некотором станке, то соответствующая стоимость cij берется равной очень большому числу. Матрица стоимостей C определяется следующим образом:
станки
виды работ 
 Прежде чем решать такую задачу необходимо ликвидировать дисбаланс, добавив фиктивные работы или станки в зависимости от начальных условий. Поэтому без потери общности можно положить m = n.
Прежде чем решать такую задачу необходимо ликвидировать дисбаланс, добавив фиктивные работы или станки в зависимости от начальных условий. Поэтому без потери общности можно положить m = n.
Пусть  = 0, если j -я работа не выполняется на i -м станке,
= 0, если j -я работа не выполняется на i -м станке,
 = 1, если j -я работа выполняется на i -м станке.
= 1, если j -я работа выполняется на i -м станке.
Таким образом, решение задачи может быть записано в виде двумерного массива  . Допустимое решение называется назначением. Допустимое решение строится путем выбора ровно одного элемента в каждой строке матрицы
. Допустимое решение называется назначением. Допустимое решение строится путем выбора ровно одного элемента в каждой строке матрицы  и ровно одного элемента в каждом столбце этой матрицы. Для заданного значения n существует n! допустимых решений.
и ровно одного элемента в каждом столбце этой матрицы. Для заданного значения n существует n! допустимых решений.
Теперь задача будет формулироваться следующим образом:

Ограничения первой группы необходимы для того, чтобы каждая работа выполнялась ровно один раз. Ограничения второй группы гарантируют, что каждому станку будет приписана ровно одна работа.
Для иллюстрации задачи о назначениях рассмотрим таблицу с тремя работами и тремя станками
Станки
| Виды работ | ||||
Специфическая структура задачи о назначениях позволяет использовать эффективный метод для ее решения.
Замечание. Оптимальное решение задачи не изменится, если из любой строки или столбца матрицы стоимостей вычесть произвольную постоянную величину. Приведеное замечание показывает, что если можно построить новую матрицу 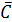 с нулевыми элементами и эти нулевые элементы или их подмножества соответствуют допустимому решению, то такое решение будет оптимальным.
с нулевыми элементами и эти нулевые элементы или их подмножества соответствуют допустимому решению, то такое решение будет оптимальным.

Оптимальное назначение:
 , остальные
, остальные 

К сожалению, не всегда удается определить решение так просто.
Венгерский алгоритм.
Шаг 1. (Редукция строк и столбцов).
Цель данного шага состоит в получении максимального возможного числа нулевых элементов в матрице стоимостей. Для этого из всех элементов каждой строки вычитают минимальный элемент соответствующей строки, а затем из всех элементов каждого столбца полученной матрицы вычитают минимальный элемент соответствующего столбца. В результате получают редуцированную матрицу стоимостей и переходят к поиску назначений.
Шаг 2. (Определение назначений)
а) Найти строки, содержащие ровно один невычеркнутый нулевой элемент. В каждой такой строке провести назначение, соответствующее невычеркнутому нулевому элементу. В каждом столбце, в котором было проведено назначение, вычеркнуть все невычеркнутые ранее нулевые элементы. Строки рассматриваются в порядке возрастания их номеров.
б) Найти столбцы, содержащие ровно один невычеркнутый элемент. В каждом таком столбце произвести назначение, соответствующее невычеркнутому новому элементу. В каждой строке, в которой было проведено назначение, вычеркнуть все невычеркнутые ранее нулевые элементы. Столбцы рассматриваются в порядке возрастания их номеров.
в) Выполнять пункты а) и б) до тех пор, пока не будет вычеркнуто максимально возможное число нулевых элементов. Если построенное назначение полное, то оно является оптимальным.
Если некоторые нули остались невычеркнутыми, то можно попытаться найти более полное назначение.
Если нельзя найти полного назначения, то необходима дальнейшая модификация матрицы стоимостей, т.е. перейти к шагу 3.
Шаг 3. (Модификация редуцированной матрицы).
Для редуцированной матрицы стоимостей:
а) Вычислить число нулей в каждой невычеркнутой строке и каждом невычеркнутом столбце.
б) Вычеркнуть строку или столбец с максимальным числом нулей.
в) Выполнять пункты а) и б) до тех пор, пока не будут вычеркнуты все нули.
г) Из всех невычеркнутых элементов вычесть минимальный невычеркнутый элемент и прибавить его к каждому элементу, расположенному на пересечении двух линий.
Перейти к шагу 2.
Замечания.
1) Если число линий, необходимое, для того чтобы вычеркнуть нулевые элементы, равно числу строк (строк), то существует полное назначение.
2) Если исходная задача является задачей максимизации, то все элементы матрицы стоимостей следует умножить на (-1) и сложить с достаточно большим числом так, чтобы матрица не содержала бы отрицательных элементов. Затем задачу следует решать как задачу минимизации.
Пример. Покажем работу венгерского алгоритма на примере задачи о назначениях со следующей матрицей стоимостей:

Итерация 1.
Шаг 1. Редукция строк и столбцов.
Значения минимальных элементов строк 1, 2, 3 и 4 равны 2, 4, 11 и 4 соответственно.
Выходя из элементов каждой строки соответствующее минимальное значение, получим следующую матрицу:

Шаг 2. Поиск допустимого решения, для которого все назначения имеют нулевую стоимость.
а) Строки 1, 2 и 4 содержат по одному невычеркнутому нулю. Рассматривая эти строки в порядке возрастания их номеров, произведем вначале назначение, соответствующее элементу (1, 1) и вычеркнем нулевой элемент (4, 1). Затем произведем назначение, соответствующее элементу (2, 2). Строка 4 не может быть использована, поскольку нулевой элемент (4, 1) был вычеркнут.
б) Столбцы 3 и 4 содержат по одному невычеркнутому нулю. Рассматривая эти столбцы в порядке возрастания их номеров, мы можем произвести третье назначение, соответствующее элементу (3, 3). В столбце 4 назначение невозможно, так как мы произвели назначение, соответствующее элементу (3, 3). После выполнения данного шага матрица стоимостей имеет следующий вид:

Таким образом, ни одно полное назначение не может быть получено, и необходимо провести дальнейшую модификацию редуцированной матрицы стоимостей.
Шаг 3. Модификация редуцированной матрицы.

а) Число нулей в строках 1, 2, 3 и 4 равно 1, 1, 2 и 1 соответственно. Для столбцов соответствующие величины равны 2, 1, 1 и 1.
б) Максимальное число нулей, по два, содержат строка 3 и столбец 1. Выбираем строку 3 и вычеркиваем все ее элементы горизонтальной линией.
в) Число невычеркнутых нулей в строках 1, 2 и 4 равно 1, 1 и 1 соответственно. Для столбцов соответствующие значения равны 2, 1, 0 и 0. Поэтому мы должны выбрать столбец 1 и вычеркнуть его вертикальной линией. После этого остается только один невычеркнутый нуль – элемент (2, 2). Поэтому можно вычеркнуть либо строку 2, либо столбец 2. Вычеркивая строку 2 горизонтальной линией, получаем следующую матрицу.

Значение минимального невычеркнутого элемента равно 2. Вычитая его из всех невычеркнутых элементов и складывая его со всеми элементами, расположенными на пересечении двух линий, получаем новую матрицу стоимостей.

Итерация 2.
Шаг 2.
Выполняя вновь процедуру допустимого решения нулевой стоимости, получаем следующее оптимальное решение:

Оптимальное назначение:
 остальные
остальные 

Пример (Задача размещения производства).
Компания разрабатывает план выпуска трех новых видов продукции. Предположим, что компания владеет пятью предприятиями и что на трех из них должны производиться новые виды продукции – по одному виду на одно предприятие. Ниже указаны издержки производства и сбыта единицы продукции.
1. Издержки производства единицы продукции (руб.):
| Предприятие | ||||||
| Вид продукции | ||||||
2. Издержки сбыта единицы продукции (руб.):
| Предприятие | ||||||
| Вид продукции | ||||||
Умножая прибыль, приходящуюся на единицу продукции, на годовой объем сбыта, можно получить общую годовую прибыль, соответствующую каждой паре вид продукции – предприятие. Данные величины (в тыс.руб.) приведены в следующей таблице:
| Предприятие | ||||||
| Вид продукции | -630 | -105 | ||||
| -11040 | -3200 | -7200 | ||||
Если прибыль рассматривать как отрицательные затраты, то исходная задача максимизации может быть сведена к задаче минимизации о назначениях. Для того чтобы матрица стоимостей не содержала отрицательных элементов, сложим каждый элемент матрицы с числом 5760 и введем два вида фиктивной продукции (4 и 5), которой соответствует нулевая прибыль. В результате будет получена следующая матрица:
| Предприятие | ||||||
| Вид продукции | -525 | -1050 | -245 | |||
| -5600 | -5760 | |||||
| -1080 | -918 | -1242 | -594 | -918 |
| Предприятие | ||||||
| Вид продукции | ||||||
 С =
С =
Итерация 1.
Шаг 1.

Шаг 2.

Шаг 3.

Итерация 2.
Шаг 2. Воспользуемся замечанием 1. Тогда получим:

Оптимальное решение данной задачи следующее: производство первого вида продукции назначается предприятию 4, второго вида – предприятию 1, третьего вида – предприятию 3, четвертого вида – предприятию 2, пятого вида – предприятию 5. Очевидно, что 2 последних назначения являются фиктивными, суммарная годовая прибыль, соответствующая данному решению, равна: 1050+5600+1242=7892 тыс. руб.
Оптимальное исследование рынка.
Группе, исследующий рынок, требуется получить данные из n различных мест. В ее распоряжении имеется n дней, и она предполагает провести по одному дню в каждом месте, проведя по  опросов
опросов  .
.
Вероятность успешного опроса в каждом месте задается матрицей P. Элемент матрицы  характеризует вероятность успешного опроса в течении
характеризует вероятность успешного опроса в течении  дня в
дня в  месте
месте  .
.
Определить время проведения опросов, при котором общее число опросов максимально.
Решение. Сведем данную задачу к задаче о назначениях.
Введем величину  , показывающую число успешных опросов в j -м месте в течение i -го дня.
, показывающую число успешных опросов в j -м месте в течение i -го дня.
Математическая модель задачи имеет следующий вид:

Функция F характеризует суммарное число успешных опросов. Ее нужно максимизировать. Первое и второе ограничения соответствуют тому, что в течение одного дня можно находиться только в одном месте. Для расчета модели венгерским методом надо перейти к противоположной функции

И в соответствующей таблице записывать значения  с противоположным знаком.
с противоположным знаком.
Оптимальное использование рабочих агентов.
Торговая фирма продает товары в n различных городах, покупательная способность жителей которых оценивается  условных единиц,
условных единиц,  . Для реализации товаров фирма располагает n торговыми агентами, каждого из которых она направляет в один из городов. Профессиональный уровень агентов различен; доля реализуемых i -м торговым агентом покупательных способностей составляет
. Для реализации товаров фирма располагает n торговыми агентами, каждого из которых она направляет в один из городов. Профессиональный уровень агентов различен; доля реализуемых i -м торговым агентом покупательных способностей составляет  ,
,  . Как следует распределить торговых агентов по городам, чтобы фирма получила максимальную выручку от продажи товаров?
. Как следует распределить торговых агентов по городам, чтобы фирма получила максимальную выручку от продажи товаров?
Решение этой проблемы может быть найдено с помощью задачи о назначениях.
В качестве кандидатов выступают торговые агенты, в качестве работ – города.
Введем параметр  , характеризующий величину покупательных способностей, реализуемых i -м агентом в j -м городе.
, характеризующий величину покупательных способностей, реализуемых i -м агентом в j -м городе.
Математическая модель записывается в следующем виде:

Первое и второе ограничения формализуют соответственно условия о том, что каждый в город направляется один торговый агент и один торговый агент не может работать в двух городах. Целевая функция F – это сумма реализованных покупательных способностей всеми торговыми агентами во всех городах. Она должна подлежать максимизации. Для решения задачи венгерским методом надо, как и в предыдущем примере, перейти к противоположной функции.
Глава 5.
Задача целочисленного линейного программирования
5.1.Постановки и методы решения
Целочисленное программирование ориентировано на решение задач математического программирования, в которых все или некоторые переменные должны принимать только целочисленные значения.
Задача называется полностью целочисленной, если условие целочисленности наложено на все ее переменные; когда это условие относится лишь к некоторым переменным, задача называется частично целочисленной. Если при этом ЦФ и функции, входящие в ограничения, линейные, то задача является линейной целочисленной.
Несмотря на то, что к настоящему времени разработан ряд методов решения целочисленных задач, ни один из них не обеспечивает желаемой эффективности соответствующих вычислительных процедур, что особенно проявляется при увеличении размерности задачи. Таким образом, в отличие от ЗЛП, время решения которых относительно невелико, реализация целочисленных алгоритмов в ряде случаев весьма затруднительна.
Одна из основных трудностей в целочисленном программировании связана с эффектом ошибки округления, возникающим при использовании цифровых ЭВМ. Даже наличие алгоритмов, применимых для решения задач с целочисленными коэффициентами и позволяющих обойтись без оперирования дробями (и, следовательно, избежать влияния ошибок округления), не упрощает ситуации, поскольку такие алгоритмы (в ряде случаев) сходятся чрезвычайно медленно.
Методы решения задач целочисленного линейного (ЗЦЛП) программирования можно условно разделить на две группы: методы отсечений, комбинаторные методы.
Исходной задачей для демонстрации возможностей методов отсечений, используемых при решении линейных целочисленных задач, является задача с ослабленными ограничениями, которая возникает в результате исключения требования целочисленности переменных. По мере введения специальных дополнительных ограничений, учитывающих требование целочисленности, многогранник допустимых решений ослабленной задачи постепенно деформируется, до тех пор пока координаты оптимального решения не станут целочисленными. Название «методы отсечений» связано с тем обстоятельством, что вводимые дополнительные ограничения отсекают (исключают) некоторые области многогранника допустимых решений, в которых отсутствуют точки с целочисленными координатами.
В основе комбинаторных методов лежит идея перебора всех допустимых целочисленных решений. Разумеется, на первый план здесь выдвигается проблема разработки тестовых процедур, позволяющих непосредственно рассматривать лишь часть (относительно небольшую) указанных решений, а остальные допустимые решения учитывать некоторым косвенным образом.
|
|