Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Задание 4.

Решить задачи с использованием искусственного базиса. Во всех задачах x 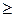0. Для каждой задачи написать двойственную задачу. Составить решение двойственной задачи по решению прямой задачи. Проверить и записать решения тех и других задач на MAPLE.

Составить двойственную задачу в общей форме к задаче

,

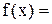
1) f = -5*x2-x3+x4-x5 → min,

-x1+x2+x3 = 2,

x1-2*x2+x4 = 2,

2*x1+x2+x3+x4+2*x5 = 11,

x1, x2, x3, x4, x5 ≥ 0.

Составим вспомогательную задачу:

U = u1+u2+u3 → min,

u1-x1+x2+x3 = 2,

u2+ x1-2*x2+x4 = 2,

u3+2*x1+x2+x3+x4+2*x5 = 11,

u1, u2, u3, x1, x2, x3, x4, x5 ≥ 0.

Из каждого равенства ограничений выражаем u1, u2, u3 через свободные переменные x1, x2, x3, x4, x5 и подставляем эти значения для целевой функции U. При такой записи вспомогательной задачи мы можем составить симплекс-таблицу:

Б.П. x1 x2 x3 x4 x5 Св. член

u1 -1.00 1.00 1.00 0.00 0.00 2.00

u2 1.00 -2.00 0.00 0.00 0.00 2.00

u3 2.00 1.00 1.00 1.00 2.00 11.00

u 2.00 0.00 2.00 2.00 2.00 15.00

Для получения следующей симплекс-таблицы воспользуемся программой D* в Турбо Паскаль. В программе D* установим константы const n=6; m=4 (число столбцов и строк). После нажатия RUN вводим через ENTER числа: -1.00 1.00 1.00 0.00 0.00 2.00 1.00 -2.00 0.00 0.00 0.00 2.00 2.00 1.00 1.00 1.00 2.00 11.00 2.00 0.00 2.00 2.00 2.00 15.00. После вводим номер разрешающего столбца j=1. Далее программа выдаст следующую симплекс-таблицу (при этом разрешающей стала вторая строка, поэтому в столбце для базисных переменных вместо u2 нужно поставить x1).

Б.П. x1 x2 x3 x4 x5 Св. член

u1 0.00 -1.00 1.00 1.00 0.00 4.00

x1 1.00 -2.00 0.00 1.00 0.00 2.00

u3 0.00 5.00 1.00 -1.00 2.00 7.00

u 0.00 4.00 2.00 0.00 2.00 11.00

Выбираем разрешающим столбцом j=2. После ввода программа выдаст следующую симплекс-таблицу (при этом разрешающей стала третья строка, поэтому в столбце для базисных переменных вместо u3 нужно поставить x2).

Б.П. x1 x2 x3 x4 x5 Св. член

u1 0.00 0.00 1.20 0.80 0.40 5.40

x1 1.00 0.00 0.40 0.60 0.80 4.80

x2 0.00 1.00 0.20 -0.20 0.40 1.40

u 0.00 0.00 1.20 0.80 0.40 5.40

Выбираем разрешающим столбцом j=3. После ввода программа выдаст следующую симплекс-таблицу (при этом разрешающей стала первая строка, поэтому в столбце для базисных переменных вместо u1 нужно поставить x3).

Б.П. x1 x2 x3 x4 x5 Св. член

x3 0.00 0.00 1.00 0.67 0.33 4.50

x1 1.00 0.00 0.00 0.33 0.67 3.00

x2 0.00 1.00 0.00 -0.33 0.33 0.50

u 0.00 0.00 0.00 0.00 0.00 0.00

Таким образом, решение найдено, поскольку u приняла оптимальное значение 0. Решив вспомогательную задачу, мы нашли базис для основной задачи. Базисом будет {А1, А2, А3}, а базисными переменными являются х1, х2, х3. Выразим базисные переменные х1, х2, х3 через свободные переменные х4, х5, используя таблицу. Получим:

x1 = -0.33*x4-0.67*x5+3

x2 = 0.33*x4-0.33*x5+0.5

x3 = -0.67*x4-0.33*x5+4.5

Подставим эти значения в выражение для функции f основной задачи. Получим:

f = -5*(.33*x4-0.33*x5+0.5)-(-0.67*x4-0.33*x5+4.5)+x4-x5 = -1.65*x4+1.65*x5-2.5+0.67*x4+0.33*x5-4.5+x4-x5 = 0.02*x4+0.98*x5-7

f-0.22*x4-0.98*x5 = -7

Теперь подставив коэффициенты для f в таблицу вместо коэффициентов для u, получим первую симплекс-таблицу для основной задачи:

Б.П. x1 x2 x3 x4 x5 Св. член

x3 0.00 0.00 1.00 0.67 0.33 4.50

x1 1.00 0.00 0.00 0.33 0.67 3.00

x2 0.00 1.00 0.00 -0.33 0.33 0.50

f 0.00 0.00 0.00 -0.22 -0.98 -7

Так как в последней строке коэффициенты для f при свободных переменных все отрицательные, то найден оптимальный план:

x1 = 3

x2 = 0.5

x3 = 4.5

x4 = 0

x5 = 0

x* = (3; 0.5; 4.5; 0; 0)

min f = -5*0.5-4.5+0-0 = -7

Проверим решение задачи, используя математическую систему MAPLE:

> with(simplex);

> minimize(-5*x2-x3+x4-x5, {-x1+x2+x3=2, x1-2*x2+x4=2, 2*x1+x2+x3+x4+2*x5=11}, NONNEGATIVE);

> subs({x3 = 0, x4 = 27/4, x5 = 0, x2 = 11/4, x1 = 3/4}, -5*x2-x3+x4-x5);

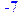
(y1) -x1+x2+x3 = 2,

(y2) x1-2*x2+x4 = 2,

(y3) 2*x1+x2+x3+x4+2*x5 = 11,

x1, x2, x3, x4, x5 ≥ 0,

f = -5*x2-x3+x4-x5 → min.

Введем три переменные y1, y2, y3 и запишем, в соответствии с правилами построения двойственных задач, двойственную задачу:

-y1+y2+2*y3 = 0,

y1-2*y2+y3 = -5,

y1+y3 = -1,

y2+y3 = 1,

2*y3 = -1,

y1, y2, y3 ≥ 0.

g(y) = 2*y1+2*y2+11*y3→ max

Согласно теореме должны выполняться следующие равенства:

y1*(-x1+x2+x3-2) = 0,

y2*(x1-2*x2+x4-2) = 0,

y3*(2*x1+x2+x3+x4+2*x5-11) = 0,

x1*(-y1+y2+2*y3) = 0,

x2*(y1-2*y2+y3+5)= 0,

x3*(y1+y3+1) = 0,

x4*(y2+y3-1) = 0,

x5*(2*y3+1) = 0.

Из решения основной задачи:

x1 = 3/4,

x2 = 11/4,

x3 = 0,

x4 = 27/4,

x5 = 0.

Найдем y1, y2, y3:

y1 = 0, y2 = 2, y3 = -1.

> subs({y2 = 2, y3 = -1, y1 = 0}, 2*y1+2*y2+11*y3);

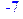
2) f = -x1+4*x2-x3-x4-x5 → min,

5*x1+5*x2+x3+2*x4+x5 = 28,

-x1+2*x2+x4 = 2,

3*x1+4*x2+x5 = 12,

x1, x2, x3, x4, x5 ≥ 0.

Составим вспомогательную задачу:

U = u1+u2+u3 → min,

u1+5*x1+5*x2+x3+2*x4+x5 = 28,

u2-x1+2*x2+x4 = 2,

u3+3*x1+4*x2+x5 = 12,

u1, u2, u3, x1, x2, x3, x4, x5 ≥ 0.

Из каждого равенства ограничений выражаем u1, u2, u3 через свободные переменные x1, x2, x3, x4, x5 и подставляем эти значения для целевой функции U. При такой записи вспомогательной задачи мы можем составить симплекс-таблицу:

Б.П. x1 x2 x3 x4 x5 Св. член

u1 5.00 5.00 1.00 2.00 1.00 28.00

u2 -1.00 2.00 0.00 1.00 0.00 2.00

u3 3.00 4.00 0.00 0.00 1.00 12.00

u 7.00 11.00 1.00 3.00 2.00 42.00

Для получения следующей симплекс-таблицы воспользуемся программой D* в Турбо Паскаль. В программе D* установим константы const n=6; m=4 (число столбцов и строк). После нажатия RUN вводим через ENTER числа: 5.00 5.00 1.00 2.00 1.00 28.00 -1.00 2.00 0.00 1.00 0.00 2.00 3.00 4.00 0.00 0.00 1.00 12.00 7.00 11.00 1.00 3.00 2.00 42.00. После вводим номер разрешающего столбца j=2. Далее программа выдаст следующую симплекс-таблицу (при этом разрешающей стала вторая строка, поэтому в столбце для базисных переменных вместо u2 нужно поставить x2).

Б.П. x1 x2 x3 x4 x5 Св. член

u1 7.50 0.00 1.00 -0.50 1.00 23.00

x2 -0.50 1.00 0.00 0.50 0.00 1.00

u3 5.00 0.00 0.00 -2.00 1.00 8.00

u 2.50 0.00 1.00 -2.50 2.00 31.00

Выбираем разрешающим столбцом j=1. После ввода программа выдаст следующую симплекс-таблицу (при этом разрешающей стала третья строка, поэтому в столбце для базисных переменных вместо u3 нужно поставить x1).

Б.П. x1 x2 x3 x4 x5 Св. член

u1 0.00 0.00 1.00 2.50 -0.50 11.00

х2 0.00 1.00 0.00 0.30 0.10 1.80

х1 1.00 0.00 0.00 -0.40 0.20 1.60

u 0.00 0.00 1.00 2.50 -0.50 11.00

Выбираем разрешающим столбцом j=4. После ввода программа выдаст следующую симплекс-таблицу (при этом разрешающей стала первая строка, поэтому в столбце для базисных переменных вместо u1 нужно поставить x4).

Б.П. x1 x2 x3 x4 x5 Св. член

x4 0.00 0.00 0.40 1.00 -0.20 4.40

x2 0.00 1.00 -0.12 0.00 0.16 0.48

x1 1.00 0.00 0.16 0.00 0.12 3.36

u 0.00 0.00 0.00 0.00 0.00 0.00

Таким образом, решение найдено, поскольку u приняла оптимальное значение 0. Решив вспомогательную задачу, мы нашли базис для основной задачи. Базисом будет {А1, А2, А4}, а базисными переменными являются х1, х2, х4. Выразим базисные переменные х1, х2, х4 через свободные переменные х3, х5, используя таблицу. Получим:

x1 = -0.16*x3-0.12*x5+3.36

x2 = 0.12*x3-0.16*x5+0.48

x4 = -0.4*x3+0.2*x5+4.4

Подставим эти значения в выражение для функции f основной задачи. Получим:

f = -x1+4*x2-x3-x4-x5 = -(-0.16*x3-0.12*x5+3.36)+4*(0.12*x3-0.16*x5+0.48)-x3-(-0.4*x3+0.2*x5+4.4)-x5 = 0.04*x3-1.72*x5-5.84

f – 0.04*x3+1.72*x5 = -5.84

Теперь подставив коэффициенты для f в таблицу вместо коэффициентов для u, получим первую симплекс-таблицу для основной задачи:

Б.П. x1 x2 x3 x4 x5 Св. член

x4 0.00 0.00 0.40 1.00 -0.20 4.40

x2 0.00 1.00 -0.12 0.00 0.16 0.48

x1 1.00 0.00 0.16 0.00 0.12 3.36

f 0.00 0.00 -0.04 0.00 1.72 -5.84

Выбираем разрешающим столбцом j=5. После ввода программа выдаст следующую симплекс-таблицу (при этом разрешающей стала вторая строка, поэтому в столбце для базисных переменных вместо х2 нужно поставить x5).

Б.П. x1 x2 x3 x4 x5 Св. член

x4 0.00 1.25 0.25 1.00 0.00 5.00

х5 0.00 6.25 -0.75 0.00 1.00 3.00

х1 1.00 -0.75 0.25 0.00 0.00 3.00

F 0.00 -10.75 1.25 0.00 0.00 -11.00

Выбираем разрешающим столбцом j=3. После ввода программа выдаст следующую симплекс-таблицу (при этом разрешающей стала третья строка, поэтому в столбце для базисных переменных вместо х1 нужно поставить x3).

Б.П. x1 x2 x3 x4 x5 Св. член

x4 -1.00 2.00 0.00 1.00 0.00 2.00

х5 3.00 4.00 0.00 0.00 1.00 12.00

х3 4.00 -3.00 1.00 0.00 0.00 12.00

f -5.00 -7.00 0.00 0.00 0.00 -26.00

Так как в последней строке коэффициенты для f при свободных переменных все отрицательные, то найден оптимальный план:

x1 = 0

x2 = 0

x3 = 12

x4 = 2

x5 = 12

x* = (0; 0; 12; 2; 12)

min f = -12-2-12 = -26

Проверим решение задачи, используя математическую систему MAPLE:

> with(simplex);

> minimize(-x1+4*x2-x3-x4-x5, {5*x1+5*x2+x3+2*x4+x5=28, -x1+2*x2+x4=2, 3*x1+4*x2+x5=12}, NONNEGATIVE);

> subs({x5 = 12, x3 = 12, x1 = 0, x4 = 2, x2 = 0}, -x1+4*x2-x3-x4-x5);

(y1) 5*x1+5*x2+x3+2*x4+x5 = 28,

(y2) -x1+2*x2+x4 = 2,

(y3) 3*x1+4*x2+x5 = 12,

x1, x2, x3, x4, x5 ≥ 0,

f = -x1+4*x2-x3-x4-x5 → min.

Введем три переменные y1, y2, y3 и запишем, в соответствии с правилами построения двойственных задач, двойственную задачу:

5*y1-y2+3*y3 = -1,

5*y1+2*y2+4*y3 = 4,

y1 = -1,

2*y1+y2 = -1,

y1+y2 = -1,

y1, y2, y3 ≥ 0.

g(y) = 28*y1+2*y2+12*y3 → max

Согласно теореме должны выполняться следующие равенства:

y1*(5*x1+5*x2+x3+2*x4+x5-28) = 0,

y2*(-x1+2*x2+x4-2) = 0,

y3*(3*x1+4*x2+x5-12) = 0,

x1*(5*y1-y2+3*y3+1) = 0,

x2*(5*y1+2*y2+4*y3-4)= 0,

x3*(y1+1) = 0,

x4*(2*y1+y2+1) = 0,

x5*(y1+y2+1) = 0.

Из решения основной задачи:

x1 = 0,

x2 = 0,

x3 = 12,

x4 = 2,

x5 = 12.

Найдем y1, y2, y3:

y1 = -1, y2 = 0, y3 = 1/6

> subs({y3 = 1/6, y1 = -1, y2 = 0}, 28*y1+2*y2+12*y3);

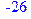
3) f = -7*x1-2*x3+x4-x5 → min,

-x1+x2+x3 = 2,

3*x1-2*x2+x4 = 3,

5*x1+2*x2+х3+х4+x5 = 11,

x1, x2, x3, x4, x5 ≥ 0.

Составим вспомогательную задачу:

U = u1+u2+u3 → min,

u1-x1+x2+x3 = 2,

u2+3*x1-2*x2+x4 = 3,

u3+5*x1+2*x2+х3+х4+x5 = 11,

u1, u2, u3, x1, x2, x3, x4, x5 ≥ 0.

Из каждого равенства ограничений выражаем u1, u2, u3 через свободные переменные x1, x2, x3, x4, x5 и подставляем эти значения для целевой функции U. При такой записи вспомогательной задачи мы можем составить симплекс-таблицу:

Б.П. x1 x2 x3 x4 x5 Св. член

u1 -1.00 1.00 1.00 0.00 0.00 2.00

u2 3.00 1.00 0.00 1.00 0.00 3.00

u3 5.00 2.00 1.00 1.00 1.00 11.00

u 7.00 4.00 2.00 2.00 1.00 16.00

Для получения следующей симплекс-таблицы воспользуемся программой D* в Турбо Паскаль. В программе D* установим константы const n=6; m=4 (число столбцов и строк). После нажатия RUN вводим через ENTER числа: -1.00 1.00 1.00 0.00 0.00 2.00 3.00 1.00 0.00 1.00 0.00 3.00 5.00 2.00 1.00 1.00 1.00 11.00 7.00 4.00 2.00 2.00 1.00 16.00. После вводим номер разрешающего столбца j=1. Далее программа выдаст следующую симплекс-таблицу (при этом разрешающей стала вторая строка, поэтому в столбце для базисных переменных вместо u2 нужно поставить x1).

Б.П. x1 x2 x3 x4 x5 Св. член

u1 0.00 1.33 1.00 0.33 0.00 3.00

x1 1.00 0.33 0.00 0.33 0.00 1.00

u3 0.00 0.33 1.00 -0.67 1.00 6.00

u 0.00 1.67 2.00 -0.33 1.00 9.00

Выбираем разрешающим столбцом j=3. После ввода программа выдаст следующую симплекс-таблицу (при этом разрешающей стала первая строка, поэтому в столбце для базисных переменных вместо u1 нужно поставить x3).

Б.П. x1 x2 x3 x4 x5 Св. член

x3 0.00 1.33 1.00 0.33 0.00 3.00

x1 1.00 0.33 0.00 0.33 0.00 1.00

u3 0.00 -1.00 0.00 -1.00 1.00 3.00

u 0.00 -1.00 0.00 -1.00 1.00 3.00

Выбираем разрешающим столбцом j=5. После ввода программа выдаст следующую симплекс-таблицу (при этом разрешающей стала третья строка, поэтому в столбце для базисных переменных вместо u3 нужно поставить x5).

Б.П. x1 x2 x3 x4 x5 Св. член

x3 0.00 1.33 1.00 0.33 0.00 3.00

x1 1.00 0.33 0.00 0.33 0.00 1.00

x5 0.00 -1.00 0.00 -1.00 1.00 3.00

u 0.00 0.00 0.00 0.00 0.00 0.00

Таким образом, решение найдено, поскольку u приняла оптимальное значение 0. Решив вспомогательную задачу, мы нашли базис для основной задачи. Базисом будет {А1, А3, А5}, а базисными переменными являются х1, х3, х5. Выразим базисные переменные х1, х3, х5 через свободные переменные х2, х4, используя таблицу. Получим:

x3 = -1.33*x2-0.33*x4+3

x1 = -0.33*x2-0.33*x4+1

x5 = x2+x4+3

Подставим эти значения в выражение для функции f основной задачи. Получим:

f = -7*x1-2*x3+x4-x5 = -7*(-0.33*x2-0.33*x4+1)-2*(-1.33*x2-0.33*x4+3)+x4-(x2+x4+3) = 2.31*x2+2.31*x4-7+2.66*x2+0.66*x4-6+x4-x2-x4-3 = 3.97*x2+2.97*x4-16

f – 3.97*x2-2.97*x4 = -16

Теперь подставив коэффициенты для f в таблицу вместо коэффициентов для u, получим первую симплекс-таблицу для основной задачи:

Б.П. x1 x2 x3 x4 x5 Св. член

x3 0.00 1.33 1.00 0.33 0.00 3.00

x1 1.00 0.33 0.00 0.33 0.00 1.00

x5 0.00 -1.00 0.00 -1.00 1.00 3.00

f 0.00 -3.97 0.00 -2.97 0.00 -16

Так как в последней строке коэффициенты для f при свободных переменных все отрицательные, то найден оптимальный план:

x1 = 1

x2 = 0

x3 = 3

x4 = 0

x5 = 3

x* = (1; 0; 3; 0; 3)

min f = -7-2*3+3 = -16

Проверим решение задачи, используя математическую систему MAPLE:

> with(simplex);

> minimize(-7*x1-2*x3+x4-x5, {-x1+x2+x3=2, 3*x1-x2+x4=3, 5*x1+2*x2+x3+x4+x5=11}, NONNEGATIVE);

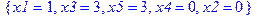
> subs({x1 = 1, x3 = 3, x5 = 3, x4 = 0, x2 = 0}, -7*x1-2*x3+x4-x5);

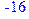
(y1) -x1+x2+x3 = 2,

(y2) 3*x1-2*x2+x4 = 3,

(y3) 5*x1+2*x2+х3+х4+x5 = 11,

x1, x2, x3, x4, x5 ≥ 0,

f = -7*x1-2*x3+x4-x5 → min.

Введем переменные y1, y2, y3, y4 и запишем, в соответствии с правилами построения двойственных задач, двойственную задачу:

-y1+3*y2+5*y3 = -7,

y1-2*y2+2*y3 = 0,

y1+y3 = -2,

y2+y3 = 1,

y3 = -1,

y1, y2, y3 ≥ 0.

g(y) = 2*y1+3*y2+11*y3→ max

Согласно теореме должны выполняться следующие равенства:

y1*(-x1+x2+x3-2) = 0,

y2*(3*x1-2*x2+x4- 3) = 0,

y3*(5*x1+2*x2+х3+х4+x5-11) = 0,

x1*(-y1+3*y2+5*y3+7) = 0,

x2*(y1-2*y2+2*y3)= 0,

x3*(y1+y3+2) = 0,

x4*(y2+y3-1) = 0,

x5*(y3+1) = 0.

Из решения основной задачи:

x1 = 1,

x2 = 0,

x3 = 3,

x4 = 0,

x5 = 3.

Найдем y1, y2, y3:

y1 = -6/5, y2 = -7/5, y3 = -4/5.

> subs({y1 = -6/5, y2 = -7/5, y3 = -4/5}, 2*y1+3*y2+11*y3);

4) f = -8*x2-2*x3-x4+x5 → min,

-x1+2*x2+x3 = 2,

6*x1+3*x2+x3+x4+x5 = 20,

3*x1-2*x2+x5 = 6,

x1, x2, x3, x4, x5 ≥ 0.

Составим вспомогательную задачу:

U = u1+u2+u3 → min,

u1-x1+2*x2+x3 = 2,

u2+6*x1+3*x2+x3+x4+x5 = 20,

u3+3*x1-2*x2+x5 = 6,

u1, u2, u3, x1, x2, x3, x4, x5 ≥ 0.

Из каждого равенства ограничений выражаем u1, u2, u3 через свободные переменные x1, x2, x3, x4, x5 и подставляем эти значения для целевой функции U. При такой записи вспомогательной задачи мы можем составить симплекс-таблицу:

Б.П. x1 x2 x3 x4 x5 Св. член

u1 -1.00 2.00 1.00 0.00 0.00 2.00

u2 6.00 3.00 1.00 1.00 1.00 20.00

u3 3.00 -2.00 0.00 0.00 1.00 6.00

u 8.00 3.00 2.00 1.00 2.00 28.00

Для получения следующей симплекс-таблицы воспользуемся программой D* в Турбо Паскаль. В программе D* установим константы const n=6; m=4 (число столбцов и строк). После нажатия RUN вводим через ENTER числа: -1.00 2.00 1.00 0.00 0.00 2.00 6.00 3.00 1.00 1.00 1.00 20.00 3.00 -2.00 0.00 0.00 1.00 6.00 8.00 3.00 2.00 1.00 2.00 28.00. После вводим номер разрешающего столбца j=1. Далее программа выдаст следующую симплекс-таблицу (при этом разрешающей стала третья строка, поэтому в столбце для базисных переменных вместо u3 нужно поставить x1).

Б.П. x1 x2 x3 x4 x5 Св. член

u1 0.00 1.33 1.00 0.00 0.33 4.00

u2 0.00 7.00 1.00 1.00 -1.00 8.00

x1 1.00 -0.67 0.00 0.00 0.33 2.00

u 0.00 8.33 2.00 1.00 -0.67 12.00

Выбираем разрешающим столбцом j=2. После ввода программа выдаст следующую симплекс-таблицу (при этом разрешающей стала вторая строка, поэтому в столбце для базисных переменных вместо u2 нужно поставить x2).

Б.П. x1 x2 x3 x4 x5 Св. член

u1 0.00 0.00 0.81 -0.19 0.52 2.48

х2 0.00 1.00 0.14 0.14 -0.14 1.14

х1 1.00 0.00 0.10 0.10 0.24 2.76

u 0.00 0.00 0.81 -0.19 0.52 2.48

Выбираем разрешающим столбцом j=3. После ввода программа выдаст следующую симплекс-таблицу (при этом разрешающей стала первая строка, поэтому в столбце для базисных переменных вместо u1 нужно поставить x3).

Б.П. x1 x2 x3 x4 x5 Св. член

x3 0.00 0.00 1.00 -0.24 0.65 3.06

x2 0.00 1.00 0.00 0.18 -0.24 0.71

x1 1.00 0.00 0.00 0.12 0.18 2.47

u 0.00 0.00 0.00 0.00 0.00 0.00

Таким образом, решение найдено, поскольку u приняла оптимальное значение 0. Решив вспомогательную задачу, мы нашли базис для основной задачи. Базисом будет {А1, А3, А5}, а базисными переменными являются х1, х2, х3. Выразим базисные переменные х1, х2, х3 через свободные переменные х4, х5, используя таблицу. Получим:

x3 = 0.24*x4-0.65*x5+3.06

x2 = -0.18*x4+0.24*x5+0.71

x1 = -0.12*x4-0.18*x5+2.47

Подставим эти значения в выражение для функции f основной задачи. Получим:

f = -8*x2-2*x3-x4+x5 = -8*(-0.18*x4+0.24*x5+0.71)-2*(0.24*x4-0.65*x5+3.06)-x4+x5 = -0.04*x4+0.38*x5-11.8

f + 0.04*x4-0.38*x5 = -11.8

Теперь подставив коэффициенты для f в таблицу вместо коэффициентов для u, получим первую симплекс-таблицу для основной задачи:

Б.П. x1 x2 x3 x4 x5 Св. член

x3 0.00 0.00 1.00 -0.24 0.65 3.06

x2 0.00 1.00 0.00 0.18 -0.24 0.71

x1 1.00 0.00 0.00 0.12 0.18 2.47

f 0.00 0.00 0.00 0.04 -0.38 -11.80

Выбираем разрешающим столбцом j=4. После ввода программа выдаст следующую симплекс-таблицу (при этом разрешающей стала вторая строка, поэтому в столбце для базисных переменных вместо х2 нужно поставить x4).

Б.П. x1 x2 x3 x4 x5 Св. член

x3 0.00 1.33 1.00 0.00 0.33 4.01

х4 0.00 5.56 0.00 1.00 -1.33 3.94

х1 1.00 -0.67 0.00 0.00 0.34 2.00

f 0.00 -0.22 0.00 0.00 -0.33 -11.96

Выразим базисные переменные х1, х4, х3 через свободные переменные х2, х5, используя таблицу. Получим:

x3 = -1.33*x2-0.336*x5+4.01

x4 = -5.56*x2+1.33*x5+3.94

x1 = 0.67*x2-0.34*x5+2

Подставим эти значения в выражение для функции f основной задачи. Получим:

f = -8*x2-2*(-1.33*x2-0.336*x5+4.01)-(-5.56*x2+1.33*x5+3.94)+x5 = 0.22*x2+0.33*x5-11.96

f – 0.22*x2-0.33*x5 = -11.96

Теперь подставив коэффициенты для f в таблицу вместо коэффициентов для u, получим первую симплекс-таблицу для основной задачи:

Б.П. x1 x2 x3 x4 x5 Св. член

x3 0.00 1.33 1.00 0.00 0.33 4.01

x4 0.00 5.56 0.00 1.00 -1.33 3.94

x1 1.00 -0.67 0.00 0.00 0.34 2.00

f 0.00 –0.22 0.00 0.00 -0.33 -11.96

Так как в последней строке коэффициенты для f при свободных переменных все отрицательные, то найден оптимальный план:

x1 = 2

x2 = 0

x3 = 4.01

x4 = 3.94

x5 = 0

x* = (2; 0; 4.01; 3.94; 0)

min f = -8*0-2*4.01-3.94+0 = -11.96

Проверим решение задачи, используя математическую систему MAPLE:

> minimize(-8*x2-2*x3-x4+x5, {-x1+2*x2+x3=2, 6*x1+3*x2+x3+x4+x5=20, 3*x1-2*x2+x5=6}, NONNEGATIVE);

> subs({x1 = 2, x4 = 4, x3 = 4, x5 = 0, x2 = 0}, -8*x2-2*x3-x4+x5);

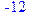
(y1) -x1+2*x2+x3 = 2,

(y2) 6*x1+3*x2+x3+x4+x5 = 20,

(y3) 3*x1-2*x2+x5 = 6,

x1, x2, x3, x4, x5 ≥ 0.

f = -8*x2-2*x3-x4+x5 → min,

Введем переменные y1, y2, y3, y4 и запишем, в соответствии с правилами построения двойственных задач, двойственную задачу:

-y1+6*y2+3*y3 = 0,

2*y1+3*y2-2*y3 = -8,

y1+y2 = -2,

y2 = -1,

y2+y3 = 1,

y1, y2, y3 ≥ 0,

g(y) = 2*y1+20*y2+6*y3→ max

Согласно теореме должны выполняться следующие равенства:

y1*(-x1+2*x2+x3- 2) = 0,

y2*(6*x1+3*x2+x3+x4+x5- 20) = 0,

y3*(3*x1-2*x2+x5- 6) = 0,

x1*(-y1+6*y2+3*y3) = 0,

x2*(2*y1+3*y2-2*y3+8)= 0,

x3*(y1+y2+2) = 0,

x4*(y2+1) = 0,

x5*(y2+y3-1) = 0.

Из решения основной задачи:

x1 = 2,

x2 = 0,

x3 = 4,

x4 = 4,

x5 = 0.

Найдем y1, y2, y3:

y1 = -18/17, y2 = -16/17, y3 = 26/17

> subs({y3 = 26/17, y2 = -16/17, y1 = -18/17}, 2*y1+20*y2+6*y3);

Составим двойственную задачу в общей форме к задаче

,

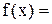
y1+y2 ≥ 1,

-5*y2 ≥ 1,

3*y1+y2 = -1,

-y1+3*y2 = 3,

y1≥ 0, y2 – произвольное,

g(y) = 7*y1+5*y2→ min