Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Задание 3. На координатной плоскости дан многоугольник ABCDE, который является областью допустимых решений задачи линейного программирования

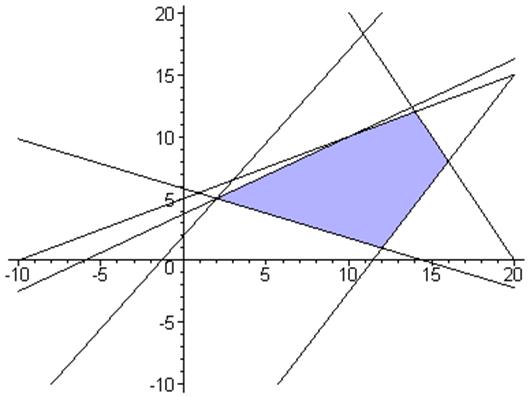
На координатной плоскости дан многоугольник ABCDE, который является областью допустимых решений задачи линейного программирования. Восстановить задачу, если известны целевая функция и координаты всех вершин многоугольника. Решить задачу графически и симплекс-методом.. Для восстановленной задачи записать двойственную и определить ее решение, используя теорему о дополняющей нежесткости. Данные

Восстановим задачу по известным целевой функции и координатам всех вершин многоугольника:

(AB): 5 x₁-10=8 x₂-40

5 x₁-8 x₂=-30

(BC): 2 x₁-20=4 x₂-40

2 x₁-4 x₂=-20

(CD): -4 x₁+56=2 x₂-24

-2 x₁-x2=-40

(DE): -7 x₁+112=-4 x₂+32

7 x₁-4 x₂=80

(EA): 4 x₁+10 x₂=58

2 x₁+5 x₂=29

Таким образом получаем задачу линейного программирования:

1. F=3x₁-2x₂®max,

5*x1-8*x2> =-30

2*x1-4*x2> =-20

-2*x1-x2> =-40

7*x1-4*x2< =80

4*x1+10*x2> =58

2. G=3x₁-2x₂®min

5*x1-8*x2> =-30

2*x1-4*x2> =-20

-2*x1-x2> =-40

7*x1-4*x2< =80

4*x1+10*x2> =58

Решим задачу графически в системе MAPLE

> with(plots); > inequal({5*x1-8*x2> =-30, 2*x1-4*x2> =-20, -2*x1-x2> =-40, 7*x1-4*x2< =80, 4*x1+10*x2> =58}, x1=-10..20, x2=-10..20, optionsexcluded = (color=white, thickness=2));

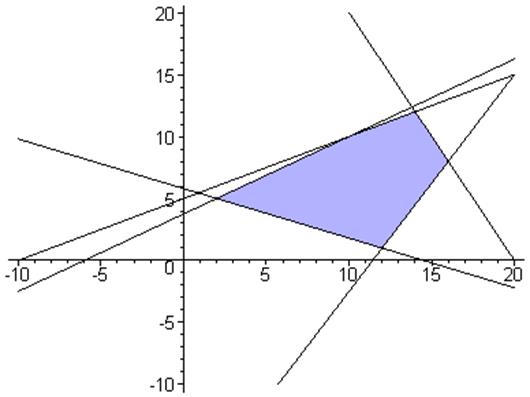
> with(simplex);

> maximize(3*x1-2*x2, {5*x1-8*x2> =-30, 2*x1-4*x2> =-20, -2*x1-x2> =-40, 7*x1-4*x2< =80, 4*x1+10*x2> =58}, NONNEGATIVE);

> subs({x2=1, x1=12}, 3*x1-2*x2);

>

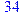
> inequal({3*x1-2*x2=34, 5*x1-8*x2> =-30, 2*x1-4*x2> =-20, -2*x1-x2> =-40, 7*x1-4*x2< =80, 4*x1+10*x2> =58}, x1=-10..20, x2=-10..20, optionsexcluded = (color=white, thickness=2));

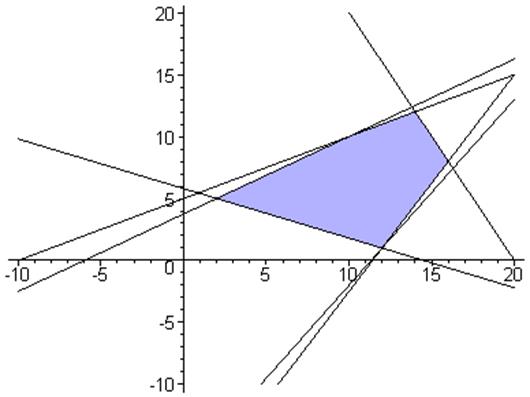
> minimize (3*x1-2*x2, {5*x1-8*x2> =-30, 2*x1-4*x2> =-20, -2*x1-x2> =-40, 7*x1-4*x2< =80, 4*x1+10*x2> =58}, NONNEGATIVE);

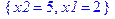
> subs({x2=5, x1=2}, 3*x1-2*x2);

> inequal({3*x1-2*x2=-4, 5*x1-8*x2> =-30, 2*x1-4*x2> =-20, -2*x1-x2> =-40, 7*x1-4*x2< =80, 4*x1+10*x2> =58}, x1=-10..20, x2=-10..20, optionsexcluded = (color=white, thickness=2));

Решим задачу симплекс-методом:

F=3x₁-2x₂®max,

5*x1-8*x2> =-30

2*x1-4*x2> =-20

-2*x1-x2> =-40

7*x1-4*x2< =80

4*x1+10*x2> =58

Составим вспомогательную задачу:

5 x₁-8 x₂> =-30

2 x₁-4 x₂> =-20

-2 x₁-x2> =-40

7 x₁-4 x_2< =80

4 x₁+10 x₂> =58

-5x1+8x2+x3=30

-2x1+4x2+x4=20

2x1+x2+x5=40

7x1-4x2+x6=80

4x1+10x2-x7=58

Из каждого равенства ограничений выражаем u1, u2, u3, u4, u5 через свободные переменные x1, x2, x3, x4, x5, x6, x7 и подставляем эти значения для целевой функции U. При такой записи вспомогательной задачи мы можем составить симплекс-таблицу: