
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
Статистический анализ в Excel.
|
|
Создаем новый лист. Переименовываем лист в «Описательная статистика». Копируем значения максимальных значений сопротивлений (в моем случае это R5). Справа вводим формулу для нахождения Р: 1/$(ссылка на Счет). Находим число сопротивлений: в ячейку Счет вводим формулу СЧЕТ(ссылка на все сопротивления). Далее задаем arg (x), который меняется от значения хmin-1 до хmax+1с шагом 0, 01. Для этого в первую строку вводим функцию хmin-1; во вторую длеаем ссылку на первую и прибавляем шаг. Далее протягиваем эти значения до значения хmax+1. Далее вводим сумму всех вероятностей, для которых х меньше чем значение arg(x). Для этого в ячейку F*(x) вводим формулу: функция СУММЕСЛИ($«ссылки на все сопротивления»; ”< ” & ЗНАЧЕН«ссылка на arg(x)»; $ «ссылка на все Р». Далее протягиваем данную формулу.
Далее используем пакет анализа Excel «Описательная статистика» (см. Рисунок 1). Для того чтобы его использовать, сначала надо его включить. Для этого нажимаем кнопку Office – параметры Excel – Надстройки - Надстройки Excel – перейти – поставить галочку на «Пакет анализа» - ок. Теперь на ленте выбираем вкладку Данные – Анализ данных. Выбираем «Описательная статистика».
Режим «Описательная статистика» служит для генерации одномерного статистического отчета по основным показателям положения, разброса и асимметрии выборочной совокупности.
В диалоговом окне данного режима задаются следующие параметры:
1. Входной интервал — Все сопротивления вместе с названием.
2. Группирование – оставляем как есть.
3. Метки в первой строке— ставим галочку.
4. Выходной интервал – ссылка на ячейку, куда выведется таблица
5. Итоговая статистика — ставим галочку. В выходном диапазоне получим по одному полю для каждого из следующих показателей описательной статистики: средняя арифметическая выборки, средняя ошибка выборки, медиана, мода, оценка стандартного отклонения по выборке, оценка дисперсии по выборке), оценка эксцесса по выборке, оценка коэффициента асимметрии по выборке, размах вариации выборки, минимальный и максимальный элементы выборки, сумма элементов выборки, количество элементов в выборке, к-й наибольший и к-й наименьший элементы выборки, предельная ошибка выборки.
6. Уровень надежности – ставим галочку. В выходной таблице включится строка для предельной ошибки выборки при установленном уровне надежности(95%).
7. К-й наибольший – Ставим галочку. В выходной таблице включится строка для к-го наибольшего значения элемента выборки. В поле, расположенное напротив флажка, введем число 2.
8. К-й наименьший — Ставим галочку. В выходной таблице включится строка для к-го наименьшего значения элемента выборки. В поле, расположенное напротив флажка, введем число 2.
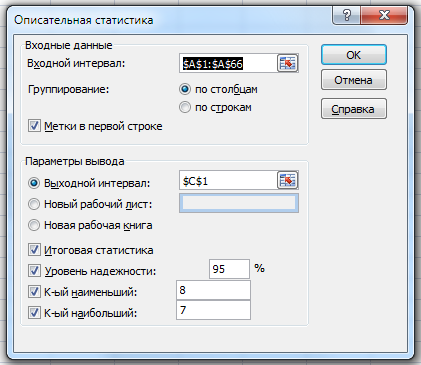
Рисунок 1 - Описательная статистика.
Получим статистический отчет по сопротивлениям в виде таблицы. В полученном отчете появятся следующие параметры:
«Среднее» - это оценка математического ожидания (рассчитывает среднюю арифметическую значений, заданных в списке аргументов).
«Стандартная ошибка» - определение средней ошибки выборки. Средняя ошибка выборки характеризует стандартное отклонение вариантов выборочной средней от генеральной средней и зависит от колеблемости признака в генеральной совокупности, числа отобранных единиц, а также от способа организации выборки.
«Медиана» - отображает значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности.
«Мода» - отображает наиболее часто встречающееся значение в интервале данных.
«Стандартное отклонение» - это корень из дисперсии;
«Дисперсия выборки» - числовая характеристика случайной величины, характеризующая рассеяние ее возможных значений около математического ожидания.
«Эксцесс» - характеризует так называемую «крутость», т. е. островершинностьили плосковершинность распределения.
«Асимметричность» - показывает распределение случайной величины относительно математического ожидания.
«Интервал» - показывает длинну интервала, в которую укладываются случайные величины (разность между максимальным и минимальным случайными величинами).
«Минимум» - находит наименьшее значение в множестве данных.
«Максимум» - находит наибольшее значение в множестве данных.
«Сумма» - находит сумму всех аргументов.
«Счет» - рассчитывает количество чисел в списке аргументов.
«Наибольший» - находит k-й по порядку наибольшее значение в множестве данных.
«Наименьший» - находит k-е по порядкунаименьшее значение в множестве данных.
«Уровень надежности» - определение коэффициента Стьюдента по заданному уровню надежности. Коэффициент Стьюдента определяет возможные пределы ошибки.
Найдем также нормальные функции распределения.
Для нахождения теоретической функциираспределения (нормальной функциейраспределения называют функцию F(x), определяющую для каждого значенияxслучайной величиныXвероятность того, что величина X примет значение, меньшее x, то есть F(x) = P(X< x)) вводим функцию НОРМРАСП («Вводим ссылку на диапозон значений arg (x)»; $«ссылка на ячейку Среднее»; $«вставляем ссылку на ячейку Стандартное отклонение»; Интегральная – ставим значение 1). Далее протягиваем формулу.
| R6 | |
| Среднее | 9, 9834375 |
| Стандартная ошибка | 0, 060890473 |
| Медиана | 10, 025 |
| Мода | 10, 12 |
| Стандартное отклонение | 0, 487123786 |
| Дисперсия выборки | 0, 237289583 |
| Эксцесс | 0, 074806799 |
| Асимметричность | -0, 229242844 |
| Интервал | 2, 38 |
| Минимум | 8, 72 |
| Максимум | 11, 1 |
| Сумма | 638, 94 |
| Счет | |
| Наибольший(1) | 11, 1 |
| Наименьший(1) | 8, 72 |
| Уровень надежности(95, 0%) | 0, 1216799 |
Постоим график выборочной функции распределения (см. Рисунок 2). Для этого заходим на вкладку «Вставка», в группу «Диаграммы», «Точечная»и выбираем «Точечная с маркерами». На вкладке «Конструктор» нажимаем «Выбрать данные» и выбираем «Диапазон данных для диаграммы»: для этого выделяем ячейки с «arg(R5)» и «F*(x)» (сумму всех вероятностей, для которых х меньше чем значение arg(x)).
Форматируем полученный график. Для этого удаляем легенду, на вкладке «Макет» выбираем «Ряд 1»– «Формат выделенного фрагмента». В появившемся окошке на вкладке «Параметры маркера» выбираем «Встроенный» и выбираем маркер «-», размер 2. Переходим на вкладку «Заливка маркера», выбираем «Сплошная заливка» и «Цвет» - черный.На вкладке «Цвет линии» выбираем «Нет линии» и на вкладке «Цвет линии маркера» выбираем «Сплошная заливка» и «Цвет» - черный. Теперь на вкладке «Макет» выбираем «Горизонтальная ось(значений)»– «Формат выделенного фрагмента». В появившемся окне на вкладке «Параметры оси» выбираем: «Минимальное значение» - «Фиксированное» - «9», «Максимальное значение» - «Фиксированное» - «15». Ставим линии сетки. Для этого на вкладке «Макет» выбираем «Сетка» - «Горизонтальные линии сетки по основной оси» («Вертикальные линии сетки по основной оси») – выбираем нужное.
На этом же графике построим теоретическую функцию распределения. Для этого заходим на вкладку «Конструктор» нажимаем «Выбрать данные» и выбираем «Добавить». В появившемся окошке выбираем «Значения Х» - выделяем ячейки с«arg(R5)»; «Значения У» - выделяем ячейки с Интегральной функциейраспределения F(x). Нажимаем «Изменить тип диаграммы» - «Точечная» и выбираем «Точечная с гладкими кривыми».
Форматируем полученный график. Для этого удаляем легенду, на вкладке «Макет» выбираем «Ряд 2»– «Формат выделенного фрагмента». В появившемся окошке на вкладке «Параметры маркера» выбираем «Нет». Переходим на вкладку «Заливка маркера», выбираем «Нет заливки». На вкладке «Цвет линии» выбираем «Сплошная линия» и «Цвет» - синий.

Рисунок 2– Графики выборочной (черной) и теоретической
|
|
