Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Задачи по физике твердого тела.

Задача 1

Выразить ширину запрещенной зоны, энергию активации доноров и акцепторов через энергетические уровни потолка валентной зоны, дна зоны проводимости, энергетических уровней доноров и акцепторов для 3 –х случаев:

а) нулевой энергетический уровень лежит внутри валентной зоны;

б) совпадает с потолком ВЗ;

в) совпадает с дном зоны проводимости.

Задача 2

Энергетический уровень орбиты наименьшего радиуса при n =1 в атоме H сосавляет -13, 6 эВ. Определить с какой длиной волны излучения связан переход электрона с этой орбиты на орбиту для которой n = 3.

Расчитать энергию залегания донорного уровня в полупроводнике у которого

величина эффективной массы электрона равна 0, 05 эВ и относительная диэлектрическая проницаемость e = 16.

Задача 3.

Для квадратной двумерной зоны Бриллюэна найти число энергетических состояний, размещающихся в углу зоны, ограниченной окружностью с радиусом 1/8 диагонали.

Задача 4.

Определить постоянную Холла в InSb при Т=300К, содержащем акцепторы с концентрацией Na = 5× 10¹⁶ см^-3, если отношение холловской подвижности к дрейфовой равно 1.18, а отношение подвижности электронов к подвижности дырок b = m_n/m_p = 80. Магнитное поле слабое, ni = 1.6× 10¹⁶ см^-3. Акцепторы считать полностью ионизованными.

Задача 5.

15.Рассчитать положение уровня Ферми для собственного полупроводника при Т=0К и Т=300К, полагая что:

а) эффективные массы электронов и дырок одинаковы;

б) Отношение эффективных масс равно 0.6.

Задача 6.

5.Найти полуширину кривой . f – функйция Ферми- Дирака.

Задача 7.

В беспримесном германии при Т=500К концентрация собственных носителей заряда равна 2.10¹⁶ см^-3. Пренебрегая зависимостью ширины запрещенной зоны от температуры определить значение произведения эффективных масс электронов и дырок: m_n* × m_p*.

Задача 8

Записать выражение для концентрации электронов и энергии Ферми в электронном полупроводнике при Ev =0.

Задача 8

Слиток получен сплавлением 100г Ge и 3.22× 10^-6 г Sb. Найти:

а) концентрацию атомов Sb, если плотность Ge – 5.46 г/см3, атомный вес Ge 72, 6, атомный вес Sb – 121, 76; б) удельное сопротивление кристалла при комнатной температуре (т =300К), если подвижность электронов и дырок соответственно равны m_n =3600 см²/В× с и m_P =1700 см²/В× с.

Задача 9

Слиток получен сплавлением 100г Ge и 3.22× 10^-6 г 0.78× 10^-6 г Ga. Найти:

а) концентрацию атомов Ga, если плотность Ge – 5.46 г/см3, атомный вес Ge 72, 6, атомный вес Ga – 121, 76;

б) удельное сопротивление кристалла при комнатной температуре (т =300К), если подвижность электронов и дырок соответственно равны m_n =3600 см²/В× с и m_P =1700 см²/В× с.

Задача 10.

Оценить интервал энергий в которм функция распределентия Ферми лежит в интеравле 0.1 – 0.9.

Задача 11

Найти зависимость концентрации электронов от температуры, если концентрация дырок изменяется по закону: Каков тип проводимости полупроводника?

Задача 12

Какова ошибка при использовании распределения Максвелла-Больцмана вместо распределения Ферми –Дирака в случаях: а) 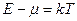, б) .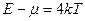

Задача 13

Найти число электронов в Ge при комнатной температуре когда уровень Ферми совпадает с дном зоны проводимости.

Задача 14

Вычислить собственные концентрации электронов Ge и Si при Т=300К. Эффективные массы плотности состояний в валентной зоне принять равными 0, 362m_o и 0, 595 m_o, и значения ширины запрещенной зоны 0, 66 эВ и 1, 1 эВ соответственно для Ge и Si.

Задача 15

Найти величину термоЭДС в Ge р- типа, содержащего 6.10¹⁵см^-3 мелких акцепторов при Т=200К. Считать, что рассеяние происходит на акустических колебаниях.

Задача 16

Постоянная Холла и удельное сопротивление равны 3.66× 10^-4 м³/Кл и 3.93× 10^-3 Ом× м соответственно.Вычислить концентрацию подвижных носителей заряда, полагая, что ток обусловлен носителями одного типа. (А_r=1).

Задача 17

Вычислить удельное сопротивление Ge и Si при температуре Т=300К. Принять значения подвижностей для этих материалов равными соответственно:

Si: m_n =1450 см²/В× с; m_p =500 см²/В× с;

Ge: m_n =3800 см²/В× с; m_P =1800 см²/В× с;

Задача 18

Образец полупроводника имеет размеры 20 х 0, 5 х 1 мм³, его удельное сопротивление r =10 Ом.см. в магнитном поле 5 кГс возникает холловское напряжение 5 мВ при токе 10 мА. Найти: концентрацию и подвижность носителей заряда, холловский угол, частоту циклотронного резонанса, время релаксации.

Задача 19

Рассчитать зависимость населенности верхнего минимума GaAs от температуры электронного газа в отсутствие вырождения. Найти чему равно отношение концентрации электронов n₂/n₁ верхнего и нижнего минимумов при Т=300К и Т=1000К. Эффективную массу плотности состояний принять равной m* =15m*. Верхний минимум находится выше на DЕ =0, 35 эВ. Полную концентрацию электронов считать независимой от температуры.

Задача 20

По температурной зависимости уровня Ферми

примесного полупроводника определить температуру, при которой m проходит через максимум.

Задача 21

Получить выражение для температуры, при которой собственная концентрация носителей равна примесной в кремнии.

Задача 22

Найти температуру, при которой происходит истощение примесей в донорном невырожденном кремнии.

Задача 23

Найти отношение концентраций легких и тяжелых дырок в кремнии р-типа.

Задача 24

Определить критическую концентрацию примеси при которой происходит переход от невырожденного к вырожденному полупроводнику при данной температуре.

Задача 25

По известным значениям концентраций носителей заряда при двух температурах n₁ = 1, 3× 10¹⁶ см^-3 при Т₁ =400К и n₂ = 6, 2× 10¹⁵ см^-3 при Т₂ =350К определить ширину запрещенной зоны.

Задача 26

По известным значениям продольной m_l и поперечной m_t эффективнs[ масс определить значения эффективной массы плотности состояний и эффективной массы проводимости.

Задача 27

При некоторой температуре в собственном кремнии подвижность носителей обращается в нуль (m =0). определить какая доля электрического тока переносится электронами. (m_n =3500 см²/Вси m_з = 1400 см²/Вс)

Задача 28

Определить значение Холл-фактора при сильном вырождении (m/кТ > 10) при рассеянии только на ионах примеси, либо только на фононах.