Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Вычислить тройной интеграл с помощью цилиндрических или сферических координат

Вычислить данные тройные интегралы.

По счастью, интеграл у нас только один. И, по счастью, пределы интегрирования явно заданы. Осталось только вычисления провести, и закончим с этим J

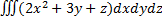, V: 2≤ x≤ 3, -1≤ y≤ 2, 0≤ z≤ 4

Ну, поехали, что ли. Не забываем две простые вещи: при интегрировании по одной из переменных все остальные считаются постоянными, и первообразная от постоянной С есть С*x. Отсюда имеем:

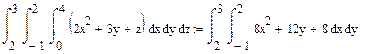
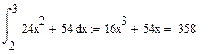
И снова сбивается шрифт, и снова какая-то мудрость с вычислениями. Хотя вроде бы все просчитал правильно, ощущение такое, что где-то есть лишняя двойка… Проверь, ок?

Вычислить тройной интеграл с помощью цилиндрических или сферических координат

Ну вот, и понеслось, как говорится. Г***о по трубам, прошу прощения за просторечие!

В нашем случае:

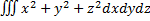, V: x²+y²+z²=4, x≥ 0, z≥ 0, y≥ 0.

В уравнении, которое ограничивает тело, трудно не узнать сферу с центром в начале координат, а поскольку все три параметра интегрирования неотрицательны, интересует нас только первая, кхем, восьмая доля пространства. Долька от арбуза, такие дела J Строить не буду, с твоего позволения: MathCad не очень-то воспринимает неявно заданные функции, а задавать поверхность вращения мне уже лень/

Итак, переходим к ядреным сферическим координатам:

Область интегрирования ограничена следующими неравенствами:

D: 0≤ θ ≤ π /2; 0≤ ρ ≤ 2; 0≤ φ ≤ π /2

Формулы перехода к сферическим координатам у тебя имеются, надеюсь. Мне просто неохота приводить их теперь J Воистину, двенадцатый час, Олик, надо закругляться и спать идти! J Давай на завершение.

Итак, после всех преобразований будем иметь:

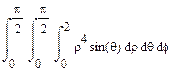
Это эквивалентно:

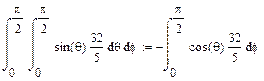
Отсюда делаем простой вывод: 32/5*φ |^{π /2}₀=32π /10, или, иначе говоря, 16π /5. С ответом совпадает, проверено J Завтра жди догона, и ложись пораньше J Спокойной ночи: *