Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Експериментальні основи теорії відносності. Постулати Ейнштейна. Перетворення Лоренца. Принцип відносності Ейнштейна.

Аналізуючи основи класичної механіки Ньютона, Ейнштейн прийшов до висновку, що уявлення про абсолютний простір і час є неправельними. У спеціальній т-ї відносності (СТВ) простір і час органічно пов’язаний між собою і з рухом матерії. В основу цієї теорії було покладено 2 постулати.

1 Всі фізичні явища у всіх інерціальних системах відліку відбуваються одноково.

2 Швидкість світла у вакуумі однакова у всіх інерціальних системах відліку і не залежить від напрямку його поширення та руху приймача та джерела.

Перший постулат є узагальненням принципу відносності Галілея на довільні фізичні явища. Всі закони і їхні рівняння є інваріантними. тобто не змінюються за формаю при переході від однієї системи до іншої. Тобто всі с-ми відліку є еквівалентними.

Другий постулат показує, що швидкість світла у вакуумі є інваріантною.

В нерятивійський механіці перехід від координат та часу однієї інерціальної с-ми до іншої здійснювався за допомогою перетворень Галілея. З цих перетворень випливає з-н складання швидкостей але якщо в с-мі світловий сигнал поширюється в напряку вектора зі швидкісттю с, то в с-мі швидкість сигналу тобто перевищеє с, звідци випливає що перетворення Галілея не справедливі і повинні бути замінені на інші.

Візьмемо дві інерціальні системи відліку , нехай в момент часу в точці знаходиться точкове джерело світла яке випромінює світло. Тді базуючись на поспулатах Ейнштейна це світло має описати свери оскільки час і простір є одномірними то залежність між 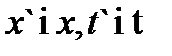повинна бути лінійною при (3) підставимо в (2): (4) це рівняння описує сферу у нерухомій с-мі відліку, отже р-ні (1, 4) повинні відповідати одне одному , , ,

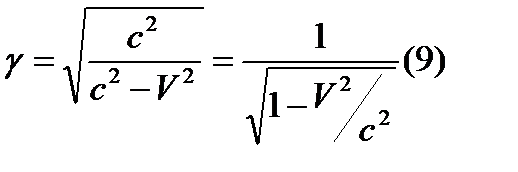
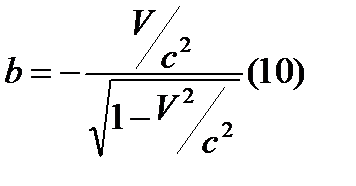
Перетворення Лоренца:

(від нерухомої системи відліку до рухомої) 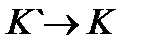(від рухомої до нерухомої)

якщо томаємо , , ,