Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Случай, когда и – комплексные параметры

Пусть , , , где – вещественные параметры. Уравнение (1) перепишем в виде

Введем новую функцию,

,

которая является регулярным решением уравнения

в област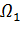и и

в области .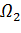

В области 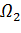перейдем к характеристическим координатам: 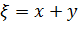и .

При этом уравнении (52) примет вид

Пусть 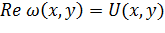и .

Тогда уравнение (51) равносильно следующей системе уравнений,

а уравнение (52) равносильно системе

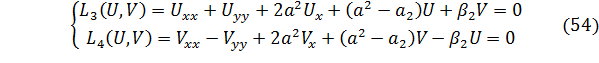
В области 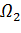перейдем к характеристическим координатам 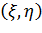, и система (54) примет вид:

Лемма. Если , и

то для любого регулярного решения уравнения (52) или системы (54) справедливо равенство

при любом .

Доказательство. Рассмотрим тождество

Из уравнения (55) и (56) выразил 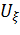и , преобразуем следующее выражение

С учетом последних преобразований тождество (57) принимает вид:

Интегрируя последнее тождество получим:

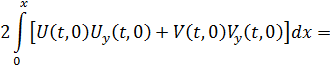
где – область, ограниченна отрезками прямых , .

Следуя роботе Сабитова К.Б. [2] можно доказать следующую теорему.

Теорема. Если в классе регулярных уравнений (1) существует решение задачи 1, то оно единственное при всех и ,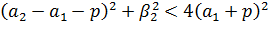

где .

ЛИТЕРАТУРА

1. Елеева В.А. Краевая задача для смешанного уравнения третьего порядка параболо-гиперболического типа – УМЖ, 1995, - Е.47, с.20-30.

2. Сабитов К.Б. О задачах Триколи для уравнения Лаврентьева – Бицадзе со спектральным параметром – ДУ, 1986 – 22, №11, с.1977-1984.

3. Сабитов К.Б. К теории уравнений смешанного параболо-гиперболического типа со спектральным параметром – ДУ, 1989 – 25, №1, с. 117-126.

4. Лепин Е.С. Курс высшей алгебры. – М.: Гостехиздат, 1953. – 345 с.

5. Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.: Наука, 1977.-735 с.

6. Векуа И.Н. Новые методы решения эллиптических уравнений. – М.: Гостехиздат, 1948. – 296 с.

7. Салахитдинов М.С., Уринов А.К. О некоторых краевых задачах уравнений смешанно типа. ДУ и вопросы ветвления. – Ташкент, ФАН, 1982. – 312 с.

8. Трикоми Ф. О линейных уравнениях смешанного типа. – М.: ОГИЗ, 1947. – 191 с.

9. Джураев Т.Д. Краевые задачи для уравнений смешанного и смешанно-составного типа. – Ташкент, ФАН, 1979. – 238 с.

10. Градштей И.С., Рыжик И.М. Таблица интегралов, суммы, рядов и произведений. – М., 1963.

11. Ректорик К. Вариационные методы в математической физике и технике. – М.: Иностранная литература, 1985. – 589 с.