
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Удк 517. 2
|
|
Федеральное агентство по образованию
Волгоградский государственный архитектурно-строительный университет
Кафедра высшей математики
Неопределенный и определенный интегралы.
Дифференциальные уравнения
Методические указания и индивидуальные задания
К контрольной работе №4
Волгоград 2010
УДК 517.2
Неопределенный и определенный интегралы. Дифференциальные уравнения: Методические указания и индивидуальные задания к контрольной работе №4 / Сост. Н.А. Болотина, К.В. Катеринин, Р.К. Катеринина, И.П. Руденок; Волгогр. гос. архит. - строит. ун-т. — Волгоград: ВолгГАСУ, 2010. — 24 c.
Содержатся краткие теоретические сведения, образец решения типового варианта контрольной работы, индивидуальные задания.
Для студентов сокращенной формы обучения ИДО всех неэкономических специальностей по дисциплине " Математика".
Библиогр. назв. 3
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
И РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ
I. Неопределённый интеграл
1. Первообразная функция и неопределённый интеграл
Определение 1. Функция F (x) называется первообразной для функции f (x) на отрезке [ a; b ], если во всех точках этого отрезка выполняется равенство:
F ¢ (x) = f (x).
Любая непрерывная функция f (x) имеет бесчисленное множество первообразных, причём все первообразные содержатся в выражении F (x)+ C, где
С — произвольная постоянная.
Определение 2. Совокупность всех первообразных функции f (x) называется неопределённым интегралом от функции f (x) и обозначается  .
.
Таким образом, по определению,
 .
.
2. Основные свойства неопределенного интеграла
1.  ;
;  .
.
2. 
3. 
4.  .
.
5. Если F (x) — первообразная функции f (x), то справедлива формула:

6. Свойство инвариантности формул интегрирования: если  , то
, то  где u – дифференцируемая функция переменной x.
где u – дифференцируемая функция переменной x.
3. Таблица основных неопределенных интегралов
1.  . .
| 2. 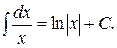
|
3. 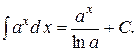 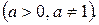
| 4. 
|
5. 
| 6. 
|
7. 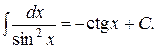
| 8. 
|
9. 
| 10. 
|
11. 
| 12.  . .
|
13. 
| |
14. 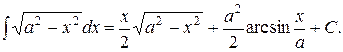
| |
15. 
|

4. Основные методы интегрирования
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
4.1. Непосредственное интегрирование
Используя тождественные преобразования подынтегральной функции и свойства неопределённых интегралов можно в ряде случаев данный интеграл свести к одному или нескольким табличным интегралам.
Пример 1. Найти 
Решение. Используя правила интегрирования (свойства 4 и 3) и табличные интегралы 4, 5, 1, получим:
 =
=  = =
= =  .
.
При интегрировании каждого слагаемого появляется своя произвольная постоянная, но в конечном итоге записываем только одну, так как сумма постоянных есть постоянная.
Правильность проведённого интегрирования можно проверить дифференцированием результата, при этом должна получиться подынтегральная функция.
Проверка:
 .
.
Пример 2. Найти 
 .
.
Решение. Выполняя деление, представим подынтегральную функцию как сумму двух функций, а затем, используя правила интегрирования 4, 3 и табличные интегралы 2, 1, получим:

 =
= 
 =
= 

 -
- 

 =
=  =
=
=  .
.
Пример 3. Найти 
 .
.
Решение. 
 =
= 
 =
= 
 =
= 
 =
=
= 
 –
– 
 =
=  .
.
Часто при сведении данного интеграла к табличному используют преобразование дифференциала, которое называют подведением под знак дифференциала и затем применяют свойство инвариантности формул интегрирования (свойство 6).
Пример 4. Найти 
 .
.
Решение. Преобразуем подынтегральную функцию:
 .
.

 =
= 
 -
- 
 =
= 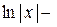

 =
= 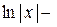
 .
.
Здесь при нахождении второго интеграла использовано преобразование дифференциала  и свойство 6.
и свойство 6.
Пример 5. Найти 
 .
.
Решение. Разлагаем подынтегральную функцию на сумму двух функций по формуле  , затем применяем преобразование дифференциала
, затем применяем преобразование дифференциала  и свойство 6. Получим:
и свойство 6. Получим: 


 = =
= = 
 =
= 

 +
+ 

 =
= 

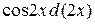 =
=
=  .
.
4.2. Метод замены переменной (метод подстановки)
Часто вычисление интеграла упрощается, если ввести новую переменную интегрирования и в качестве такой новой переменной выбрать некоторую функцию z =ψ (x), входящую в подынтегральное выражение. Это целесообразно делать в тех случаях, когда множитель dz =ψ '(x) dx также находится в составе подынтегрального выражения.
Формула замены переменной при такой подстановке имеет вид:
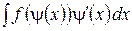 =
= 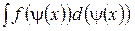 =
=  . (1)
. (1)
Формулу (1) можно читать «справа налево», т.е. подбирать подстановку в виде  :
:
 .
.
Пример 6. Найти  .
.
Решение. Наличие множителя xdx даёт возможность применить подстановку z=x2 +1. Дифференцируя, получим dz = 2 x dx, x dx =  dz, следовательно,
dz, следовательно,  .
.
Пример 7. Найти  .
.
Решение. Введём подстановку z = arctg x. Эта замена целесообразна, так как под интегралом содержится дробь  . Тогда
. Тогда 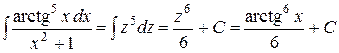 .
.
4.3. Метод интегрирования по частям
Пусть u (x) и v (x) — дифференцируемые функции. Формула
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
 = u v -
= u v -  (2)
(2)
называется формулой интегрирования по частям. Этой формулой пользуются в тех случаях, когда интеграл  более простой по сравнению с заданным интегралом
более простой по сравнению с заданным интегралом  .
.
Пользуясь формулой (2), весьма важно правильно выбрать множители u и dv. Для разложения подынтегрального выражения на указанные множители нет общих правил. Вместе с тем можно руководствоваться следующими указаниями.
Если подынтегральное выражение содержит произведение показательной или тригонометрической функции на многочлен, то за множитель u следует принять многочлен.
Если подынтегральное выражение содержит произведение логарифмической или обратной тригонометрической функции на многочлен, то за множитель u следует принять логарифмическую или обратную тригонометрическую функцию.
Пример 8. Найти  .
.
Решение. Принимаем u= 2 х –5, dv =  . Тогда
. Тогда  ,
, 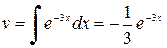 . Применяя формулу (2) получим:
. Применяя формулу (2) получим:
 =
= 
=  .
.
Следует отметить, что при определении функции v по дифференциалу dv можно брать любую произвольную постоянную, так как в конечный результат она не входит. Поэтому удобно принять С =0.
Пример 9. Найти  .
.
Решение. 
=  .
.
Рассмотренные выше методы вычисления неопределённых интегралов не дают общего правила для интегрирования любой функции. Однако можно выделить несколько классов функций (дробно-рациональные, тригонометрические и др.), интегралы от которых можно вычислять стандартными методами [1], [2], [3].
II. Определённый интеграл
1. Основные свойства определенного интеграла
1.  .
.
2.  .
.
3.  .
.
4. 
5.  — свойство аддитивности.
— свойство аддитивности.
6. Если f (x) ³ 0 на [ a, b ], то  .
.
2. Формула Ньютона – Лейбница
Формула Ньютона – Лейбница является основной формулой интегрального исчисления, она позволяет вычислить определённый интеграл от любой функции f (x), для которой известна первообразная F (x):
 . (3)
. (3)
Разность F (b)- F (a) принято обозначать знаком двойной подстановки F (x)  , поэтому формулу Ньютона-Лейбница можно записать и так:
, поэтому формулу Ньютона-Лейбница можно записать и так:  = F (x)
= F (x)  .
.
Пример 10. Вычислить  .
.
Решение. Используя свойства 4 и 3, а при нахождении первообразных табличные интегралы 2 и 1, получим:
 =
=  = =4
= =4 
3. Метод замены переменной в определённом интеграле
При использовании подстановки в определённом интеграле подынтегральное выражение преобразуется так же, как и в случае неопределённого интеграла. Особенность заключается в том, что нет необходимости возвращаться к прежней переменной. Достаточно дополнительно произвести замену пределов интегрирования, определив интервал, который должна пройти новая переменная.
Пример 11. Вычислить  .
.
Решение. Преобразуем подынтегральное выражение:
 . Применим подстановку:
. Применим подстановку:  , тогда
, тогда  . Определим новый промежуток интегрирования. Если
. Определим новый промежуток интегрирования. Если  то
то  и t = 1; если
и t = 1; если  , то
, то  = t и t = 0. Значит,
= t и t = 0. Значит,  Положительный знак перед последним интегралом взят в соответствии со свойством 2, при этом верхний и нижний пределы интегрирования поменялись местами.
Положительный знак перед последним интегралом взят в соответствии со свойством 2, при этом верхний и нижний пределы интегрирования поменялись местами.
4. Интегрирование по частям в определённом интеграле
Формула
 (4)
(4)
называется формулой интегрирования по частям в определённом интеграле.
Пример 12. Вычислить  .
.
Решение.  =
=  =
=
=  =
=  .
.
5. Интегралы с бесконечными пределами
Пусть функция ƒ (х) непрерывна на промежутке [ a, +∞). Если интеграл  при в → ∞ имеет конечный предел, то этот предел называют несобственным интегралом и обозначают
при в → ∞ имеет конечный предел, то этот предел называют несобственным интегралом и обозначают  . При этом говорят, что несобственный интеграл существует или сходится.
. При этом говорят, что несобственный интеграл существует или сходится.
Таким образом, по определению,
 .
.
Если же указанный предел не существует или он бесконечен, то говорят, что интеграл  не существует или расходится.
не существует или расходится.
Аналогично определяется несобственный интеграл на промежутке (-∞; в ]:
 .
.
Пример 13.

=  .
.
Пример 14.
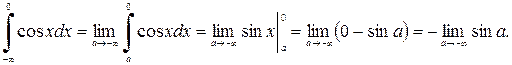
Так как предел  не существует, то данный интеграл расходится.
не существует, то данный интеграл расходится.
6. Вычисление площади плоской фигуры
Площадь фигуры, ограниченной кривыми  и
и 
 и прямыми х=а, х=в (рис.1) находится по формуле:
и прямыми х=а, х=в (рис.1) находится по формуле:
 (5)
(5)

|
|














|
|





 В случае, когда данная фигура ограничена только двумя кривыми
В случае, когда данная фигура ограничена только двумя кривыми  и
и  (рис. 2), прежде всего следует найти абсциссы точек пересечения этих кривых х1 = а и х2 = в. После этого для вычисления площади такой фигуры можно использовать формулу (5).
(рис. 2), прежде всего следует найти абсциссы точек пересечения этих кривых х1 = а и х2 = в. После этого для вычисления площади такой фигуры можно использовать формулу (5).
Пример 15. Вычислить площадь фигуры, ограниченной линиями у=х
и у= 2- х2.
Решение. Найдём точки пересечения прямой у = х с параболой у =2– х 2.
Для этого решим систему уравнений: 
Значение у=х из первого уравнения подставим во второе, получим:
х= 2– х 2, откуда найдём х 1=-2, х 2=1. Тогда из первого уравнения у 1=-2, у 2=1.
 Следовательно, линии пересекаются в точках А (-2; -2) и В (1; 1) (рис. 3).
Следовательно, линии пересекаются в точках А (-2; -2) и В (1; 1) (рис. 3).
Искомая площадь, согласно формуле (5), равна:



III. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
1. Основные понятия
Определение 3. Уравнение вида
F (x, y, y¢) = 0 (6)
где х — независимая переменная, у — искомая функция, у ¢ — ее производная, называется дифференциальным уравнением первого порядка.
Решением дифференциального уравнения (6) называется всякая функция у= φ (х), которая при подстановке в уравнение обращает его в тождество.
Дифференциальное уравнение первого порядка имеет бесчисленное множество решений. Общим решением уравнения (6) называется такое решение у= φ (х, С), которое при любом значении произвольной постоянной С удовлетворяет этому уравнению.
Решение, которое получается из общего решения при некотором конкретном числовом значении С=С0 называется частным решением.
Частное решение имеет вид у = φ (х, С0). Чтобы найти С0 задаётся начальное условие у= у 0 при х= х 0, которому должно удовлетворять искомое частное решение.
2. Дифференциальные уравнения с разделяющимися переменными
Определение 4. Дифференциальным уравнением с разделяющимися переменными называется уравнение вида:
М (x) N (y) dx + P (x) Q (y) dy =0. (7)
Разделив обе части уравнения (7) на произведение P (x) N (y) получим уравнение с разделёнными переменными:
 . (8)
. (8)
Почленное интегрирование уравнения (8) приводит к выражению:
 ,
,
которое в неявной форме определяет решение исходного уравнения и называется общим интегралом этого уравнения.
Пример 16. Решить уравнение  х dx + y (4 + x 2) dy =0.
х dx + y (4 + x 2) dy =0.
Решение. Разделим обе части уравнения на (4+ x 2)  . Получим:
. Получим:

Выполняем интегрирование:
 ,
, 
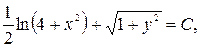
 .
.
Полученное выражение есть общий интеграл данного уравнения.
3. Линейные уравнения первого порядка. Уравнение Бернулли
Определение 5. Уравнение вида
у¢ + р (х) у = f (x), (9)
где р (х) и f (x) — непрерывные функции, называется линейным дифференциальным уравнением первого порядка.
Будем искать решение у (х) уравнения (9) в виде произведения двух функций у (х)= U (x) V (x). Тогда у ¢ = U ¢ (x) V (x)+ U (x) V ¢ (x) и уравнение (9) примет вид:
U ¢ V + UV ¢ + p (x) UV = f (x), или
U ¢ V + U (V ¢ + p (x) V)= f (x).
Выберем функцию V такой, чтобы выражение в скобке V ¢ + p (x) V равнялось нулю. Тогда получим два уравнения с разделяющимися переменными:
V ¢ + p (x) V =0 и U ¢ V = f (x).
Решая первое уравнение находим V= V (x), причём достаточно взять частное решение, когда произвольная постоянная равна 0. Подставив найденное значение V (x) во второе уравнение и решив его, найдём U (x, C). Возвращаясь к переменной у получим общее решение уравнения (9) у (х)= U (x, С) V (x).
К линейным уравнениям приводятся уравнения Бернулли, которые отличаются от линейных наличием в правой части, кроме функции f (x), ещё и множителя уп, где п ≠ 0, п ≠ 1. Общий вид такого уравнения:
у ¢ + р (х) у = f (x) y n.
На практике при решении уравнений Бернулли их не сводят к линейным, а интегрируют, как и линейные, подстановкой у (х)= U (x) V (x).
Пример 17. Решить уравнение у ¢ +  = у2х.
= у2х.
Решение. Дано уравнение Бернулли. Сделав замену у = UV, у ¢ = U ¢ V + UV ¢, получим: U ¢ V + UV ¢ +  =(UV)2 х или U ¢ V + U (V ¢ +
=(UV)2 х или U ¢ V + U (V ¢ +  )= U2V2х.
)= U2V2х.
Приравнивая к нулю выражение в скобках, получим два уравнения:
V ¢ +  = 0 и U ¢ V = U 2 V 2х.
= 0 и U ¢ V = U 2 V 2х.
Решаем первое уравнение. V ¢ +  = 0,
= 0,  ,
, 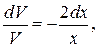
 , V =
, V =  .
.
Подставим найденное значение V во второе уравнение и решим его:
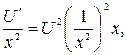



 U =
U =  .
.
Значения U (x) и V (x) подставим в решение у = U V. Получим:
у =  — это и есть общее решение данного уравнения.
— это и есть общее решение данного уравнения.
РЕШЕНИЕ ТИПОВОГО ВАРИАНТА
1. Найти неопределённые интегралы:
а)  , б)
, б)  , в)
, в)  .
.
В пунктах а) и б) результаты проверить дифференцированием.
Решение. а) Введём подстановку t = - x 2.Тогда dt = - 2 x dx, xdx = -  dt.
dt.
 =
=  =
= 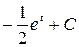 =
=  .
.
Проверка. 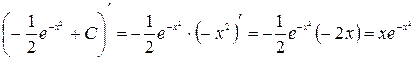 .
.
б) Применим метод интегрирования по частям, тогда
 =
=  =
=  =
=
= 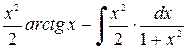 =
=  =
=
=  =
= 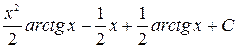 =
=
=  .
.
Проверка. ( )' =
)' =  .
.
в) Из квадратного трёхчлена знаменателя выделим полный квадрат:

Тогда  .
.
Введём подстановку  . Получим:
. Получим:

=  .
.
2. Вычислить несобственный интеграл  или установить его расходимость.
или установить его расходимость.
Решение.  =
= 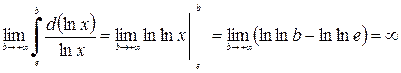 .
.
Следовательно, данный интеграл расходится.
3. Вычислить площадь фигуры, ограниченной линиями у = 2 х – х 2, у = 2 х,
х = 0, х = 2.
Решение. Данная фигура ограничена сверху графиком показательной функции у = 2 х, снизу – параболой у = 2 х – х 2, с боков – отрезками прямых х = 0, х = 2, параллельных оси Оу (Рис.4).
|





|





|







|

|





|
|

|
Следовательно, S = 
= 
4. Найти общее решение дифференциального уравнения  и частное решение, удовлетворяющее начальному условию у0 = 1 при х0 = π.
и частное решение, удовлетворяющее начальному условию у0 = 1 при х0 = π.
Решение. Данное уравнение является линейным, поэтому его можно решить с помощью подстановки у = UV, у ¢ = U ¢ V + UV ¢.
Тогда данное уравнение примет вид:
U ¢ V + UV ¢ + UV tg x =  , или V (U ¢ + U tg x) + U V ¢ =
, или V (U ¢ + U tg x) + U V ¢ =  .
.
Полагая выражение в скобке равным нулю, получим два уравнения:
U ¢ + U tg x =0 и U V ¢ =  .
.
Решаем первое уравнение:  + U tg x = 0,
+ U tg x = 0,  ,
,
 ,
, 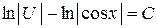 .
.
При С = 0 получим частное решение U = cos x, подставим его во второе уравнение и решим полученное уравнение:
cos x  =
=  ,
,  , V = tg x + C.
, V = tg x + C.
Общее решение исходного уравнения у = U V = cos x (tg x + C). Из него выделим частное решение, удовлетворяющее начальному условию у (π) = 1: 1 = cos π (tg π + C), 1 = - 1 (0 + С), откуда С = - 1. Подставляя значение
С = -1 в общее решение, получим частное решение исходного уравнения:
у = cos x (tg x - 1) = sin x – cos x.
ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
1. Найти неопределенные интегралы. В пунктах а) и б) результаты проверить дифференцированием.
1. а)  б)
б)  ; в)
; в) 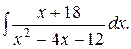
2. а)  б)
б)  ; в)
; в) 
3. а)  б)
б)  ; в)
; в) 
4. а)  б)
б)  ; в)
; в) 
5. а) 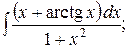 б)
б)  ; в)
; в) 
6. а)  б)
б)  ; в)
; в) 
7. а)  б)
б)  ; в)
; в) 
8. а)  б)
б)  ; в)
; в) 
9. а)  б)
б)  ; в)
; в) 
10. а)  б)
б) 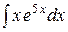 ; в)
; в) 
11. а)  б)
б)  ; в)
; в) 
12. а) 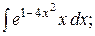 б)
б)  ; в)
; в) 
13. а)  б)
б)  ; в)
; в) 
14. а)  б)
б)  ; в)
; в) 
15. а) 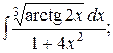 б)
б)  ; в)
; в) 
16. а)  б)
б)  ; в)
; в) 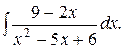
17. а)  б)
б)  ; в)
; в) 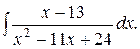
18. а)  б)
б)  ; в)
; в) 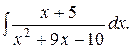
19. а)  б)
б)  ; в)
; в) 
20. а)  б)
б)  ; в)
; в) 
21. а)  б)
б)  ; в)
; в) 
22. а)  б)
б)  ; в)
; в) 
23. а) 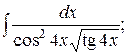 б)
б) 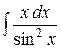 ; в)
; в) 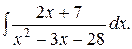
24. а)  б)
б)  ; в)
; в) 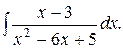
25. а) 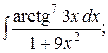 б)
б)  ; в)
; в) 
26. а)  б)
б)  ; в)
; в) 
27. а) 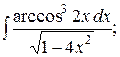 б)
б)  ; в)
; в) 
28. а)  б)
б)  ; в)
; в) 
29. а) 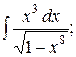 б)
б)  ; в)
; в) 
30. а)  б)
б)  ; в)
; в) 
2. Вычислить несобственный интеграл или установить его расходимость.
1.  .
.
2.  .
.
3.  .
.
4.  .
.
5. 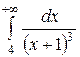 .
.
6.  .
.
7.  .
.
8.  .
.
9.  .
.
10.  .
.
11.  .
.
12.  .
.
13.  .
.
14.  .
.
15.  .
.
16.  .
.
17.  .
.
18.  .
.
19.  .
.
20. 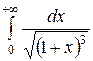 .
.
21.  .
.
22. 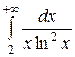 .
.
23.  .
.
24.  .
.
25.  .
.
26.  .
.
27.  .
.
28.  .
.
29.  .
.
30.  .
.
3. Вычислить площадь фигуры, ограниченной линиями:
1. 3 x 2 – 4 y = 0, 2 x – 4 y + 1 = 0.
2. y = x 3 + 3, x = 0, y = x – 1, x = 2.
3. 
 x = 4, y = 0.
x = 4, y = 0.
4. 4 x – 3 y 2 = 0, 4 x + 2 y – 1 = 0.
5. y = x 3 – 2, x = 0, y = x + 2, x = –3.
6.  , y = x.
, y = x.
7. 2 x + 3 y 2 = 0, 2 x + 2 y + 1 = 0.
8. y = x 3 – 1, x = 0, y = x + 3, x = –2.
9. x y = 6, x + y – 7 = 0.
10. 3 x 2 – 2 y = 0, 2 x + 2 y – 1 = 0.
11. y = x 3 + 1, x = 0, y = x + 5, x = –2.
12. y = 7 x 2, y = 1 + 2 x – x 2.
13. 2 x – 3 y 2 = 0, 2 x + 2 y – 1 = 0.
14. y = x 3 + 2, x = 0, y = x + 6, x = –2.
15. 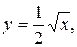
 y = 2, x = 0.
y = 2, x = 0.
16. 4 x + 3 y 2 = 0, 4 x + 2 y + 1 = 0.
17. y = x 3 + 3, x = 0, y = x + 7, x = –2.
18. y = x + 1, y = cos x, y = 0 (x ≤ 0).
19. 3 x 2 + 4 y = 0, 2 x – 4 y – 1 = 0.
20. y = x 3 – 2, x = 0, y = x – 6, x = 2.
21. x y = 4, x + y – 5 = 0.
22. 3 x 2 – 4 y = 0, 2 x + 4 y – 1 = 0.
23. y = x 3 – 1, x = 0, y = x – 5, x = 2.
24. y = 2 x, y = 2 x – x 2, x = 0, x = 2.
25. 3 x 2 – 2 y = 0, 2 x – 2 y + 1 = 0.
26. y = x 3 + 2, x = 0, y = x – 2, x = 2.
27. y = – 3 x 2 – 3 x, y + 9 x + 9 = 0.
28. 3 x 2 + 4 y = 0, 2 x + 4 y + 1 = 0.
29. y = x 3 + 1, x = 0, y = x – 3, x = 2.
30. y = – x 2 + 4, 2 x + y – 4 = 0.
4. Найти общее решение дифференциального уравнения и частное
решение, удовлетворяющее начальному условию: y = y0 при x = x0.
1.  y 0 = 0, x 0 =
y 0 = 0, x 0 =  .
.
2.  y 0 = 3, x 0 =
y 0 = 3, x 0 =  .
.
3.  y 0 = 1, x 0 = 3.
y 0 = 1, x 0 = 3.
4.  y 0 = 2, x 0 = 0.
y 0 = 2, x 0 = 0.
5.  y 0 =
y 0 =  , x 0 = – 1.
, x 0 = – 1.
6.  y 0 = 2, x 0 = 1.
y 0 = 2, x 0 = 1.
7.  y 0 = 5, x 0 = -2.
y 0 = 5, x 0 = -2.
8.  y 0 = 1, x 0 = π.
y 0 = 1, x 0 = π.
9.  y 0 = 0, x 0 = e.
y 0 = 0, x 0 = e.
10.  y 0 = 4, x 0 = 0.
y 0 = 4, x 0 = 0.
11.  y 0 = 1, x 0 = 0.
y 0 = 1, x 0 = 0.
12. 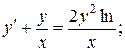 y 0 =
y 0 =  , x 0 = 1.
, x 0 = 1.
13.  y 0 = 3, x 0 = 0.
y 0 = 3, x 0 = 0.
14. 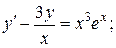 y 0 = e, x 0 = 1.
y 0 = e, x 0 = 1.
15.  y 0 = e, x 0 = 1.
y 0 = e, x 0 = 1.
16.  y 0 = 2, x 0 = 0.
y 0 = 2, x 0 = 0.
17.  y 0 =
y 0 = 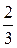 , x 0 = 0.
, x 0 = 0.
18.  y 0 = 1, x 0 = 0.
y 0 = 1, x 0 = 0.
19.  y 0 = 1, x 0 =
y 0 = 1, x 0 =  .
.
20. 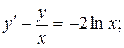 y 0 = 1, x 0 = 1.
y 0 = 1, x 0 = 1.
21.  y 0 = 1, x 0 = 3.
y 0 = 1, x 0 = 3.
22.  y 0 = 3, x 0 = 0.
y 0 = 3, x 0 = 0.
23.  y 0 = 0, x 0 =
y 0 = 0, x 0 =  .
.
24.  y 0 = 2, x 0 = 0.
y 0 = 2, x 0 = 0.
25.  y 0 = 1, x 0 = 0.
y 0 = 1, x 0 = 0.
26.
| <== предыдущая лекция | | | следующая лекция ==> |
| Информационное обеспечение обучения | | | Новинка! 2 тура по цене одногоЭкскурсионный тур выходного дня 2 ночи/1день |
