Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
Параллакс светила
|
|
Параллаксом называется его кажущееся смещение, обусловленное перемещением наблюдателя. Вследствие данного явления направления из разных точек земной поверхности на светила солнечной системы не будут параллельными. Поэтому наблюдения, сделанные в один и тот же момент в разных точках земной поверхности, не будут сравнимы между собой. Очевидно, и наблюдения, сделанные в одной и той же точке, но через некоторый промежуток времени, так же не будут сравнимы между собой, так как вследствие суточного вращения Земли вокруг своей оси место наблюдателя переместится за этот промежуток времени в другую точку пространства. Следовательно, явление параллакса для тел солнечной системы связанно с суточным вращением Земли.
Для того, чтобы сравнить наблюдения светил между собой в астрономии принято небесные координаты светил относить к центру Земли, т.е. к точке, которая принимает участия в суточном вращении Земли.
Допустим, что из точки А земной поверхности наблюдатель усматривает светило S по направлению AS (рисунок 14). Переместим мысленно наблюдателя из точки А в центр Земли О. Очевидно, что из центра Земли он будет усматривать то же самое светило по направлению OS. Проведем через точку А прямую AS’, параллельную направлению OS. Полученный угол SAS’ представляет собой величину изменения направления на светило вследствие перемещения наблюдателя из точки А в точку О.
| z |
| Истинный горизонт |
| S |
| S' |
| O |
| A |
| PA |
| h |
| hсв |
| R |
| Истинный Горизонт, приведенный к центру земли |
| PA |
Рисунок 14 — Явление параллакса
Поэтому параллакс светила — это угол (PA), под которым со светила усматривается перемещение наблюдателя АО, равное радиусу Земли. Обозначим через hcв высоту светила над истинным горизонтом, измеренную из точки А, буквой h — геоцентрическую, или истинную высоту светила. Из рисунка видно, что когда светило находится на горизонте (hcв=0), влияние параллакса достигает наибольшей величины. В этом случае он называется горизонтальным параллаксом (НР) светила. Практическая разница между полярным и экваториальным горизонтальными параллаксами незначительна и достигает лишь 0 ’, 3 (у Луны). Поэтому при составлении мореходных таблиц для всех наблюдателей в расчет принимается экваториальный горизонтальный параллакс Луны. В общем случае параллакс светила можно выразить по формуле:
;
Величина горизонтального экваториального параллакса НР зависит от расстояния до светила.
У светил солнечной системы он меняется в определенных границах, данные о которых сведены в таблицу 2.
Таблица 2 — Диапазон изменения горизонтального параллакса некоторых светил солнечной системы
| Светило | Горизонтальный параллакс |
| Солнце | от 8 '', 8 до 0 ', 15 |
| Луна | от 53 ', 5 до 61 ', 5 |
| Венера | от 0 ', 1 до 0 ', 55 |
| Марс | от 0 ', 1 до 0 ', 4 |
Значения горизонтального параллакса для Луны приводятся в ежедневных таблицах морского астрономического ежегодника (Nautical Almanac) с точностью до 0 ', 1, и их величины даются на каждый час UTC.
Как видно из таблицы значения параллакса для Солнца и планет не велики и, как правило, уже учтены в таблицах общей поправки измеренных высот (Приложение Б).
Значением параллакса для звезд, вследствие их большой удаленности, можно пренебречь.
3. Наклонение видимого горизонта
Вследствие действия земной рефракции горизонт будет несколько приподнят и изобразится малым кругом (рисунок 15). Луч из точки c’ придет к глазу наблюдателя по кривой c’А, и наблюдатель будет усматривать любую точку на горизонте cc’ по касательной к этой кривой АВ из точки А — видимый горизонт. Угол между плоскостью истинного горизонта (АН) и направлением на видимый горизонт (АВ) называется наклонением видимого горизонта d(DIP).
Из рисунка видно, что d увеличивает высоту светила, а поэтому значение d, как поправки, в большинстве случаев отрицательное, величина наклонения горизонта зависит от высоты глаза наблюдателя и от состояния атмосферы. SAН, обозначаемый на черте буквой hсв, представляет собой искомую высоту светила, а угол SAB, обозначенный через h, представляет видимую высоту светила.
| S |
| c’ |
| c |
| Истинный горизонт |
| O |
| A |
| z |
| d |
| b |
| h |
| hсв |
| D |
| Видимый горизонт |
| b’ |
| В |
| Н |
Рисунок 15 — Наклонение видимого горизонта
Для приближенных расчетов значения d, выраженного в минутах, служит формула:
;
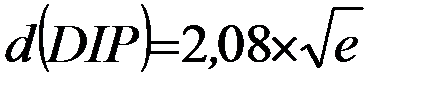где e — высота глаза наблюдателя в метрах.
В мореходных таблицах и астрономическом ежегоднике приводится специальная таблица, где даны значения d(DIP) (Приложение Б, таблица Б2) в зависимости от высоты глаза наблюдателя для средних условий: t= + 10° С и Р = 760 мм.
4. Полудиаметр светила
При наблюдении Солнца и Луны, которые представляются нам в виде дисков различной угловой величины, обычно измеряют высоту верхнего или нижнего края диска светила. Поэтому для определения высоты центра светила к измеренной высоте надо придать с нужным знаком величину видимого полудиаметра Солнца или Луны.
Допустим, что на рисунке 16 в точке А земной поверхности находится наблюдатель, АН — линия истинного горизонта, S — светило (Солнце, Луна). Наблюдатель измеряет высоту верхнего или нижнего края диска, которая будет отличаться от истинной высоты hсв на величину полудиаметра светила, т.е. на величину угла SAb (SAb’) — радиуса светила.
| Истинный горизонт |
| A |
| z |
| hсв |
| b’ |
| Н |
| S |
| b |
Рисунок 16 — Полудиаметр светила
Из рисунка видно, что при измерении высоты нижнего края светила полудиаметр SD прибавляется к видимой высоте, а при измерении высоты верхнего края диска светила — вычитается из видимой высоты верхнего края Солнца. Значения полудиаметров Солнца приводятся на каждые три дня в ежедневных таблицах (Nautical Almanac), а для Луны — на каждые 24ч, с точностью до 0', 1. В зависимости от расстояния до светила видимый полудиаметр Солнца в течение года меняется от 15', 8, когда Земля около 2 июля проходит через Афелий, до 16', 3, когда Земля около 1 января находится в Перигелии. В среднем полудиаметр Солнца принимают равным 16'. Полудиаметр Луны меняется в пределах от 14', 7 в Апогее до 16', 7 в Перигее. В среднем он равен 15', 7.
|
|