Работа силы (сил) над одной точкой

§ Работа нескольких сил определяется естественным образом как работа их равнодействующей (их векторной суммы). Поэтому дальше будем говорить об одной силе.

При прямолинейном движении одной материальной точки и постоянном значении приложенной к ней силы работа (этой силы) равна произведению величины проекции вектора силы на направление движения и величины совершённого перемещения^[3]:

Здесь точкой обозначено скалярное произведение^[4], — вектор перемещения; подразумевается, что действующая сила постоянна в течение всего того времени, за которое вычисляется работа.

Кінети́ чна ене́ ргія — частина енергії фізичної системи, яку вона має завдяки руху.

Кінетичну енергію заведено позначати буквами або .

У випадку частинки із масою та швидкістю кінетична енергія дається формулою

Кінетична енергія залежить від системи відліку, оскільки від неї залежить швидкість. Справді, для спостерігача, що рухається паралельно з тілом, за яким ведеться спостереження, тіло здається непорушним, а, отже, не має кінетичної енергії. Для спостерігача в іншій системі відліку це тіло рухається, а, отже, небезпечне при зіткненні.

Потенціа́ льна ене́ ргія — частина енергії фізичної системи, що виникає завдяки взаємодії між тілами, які складають систему, та із зовнішніми щодо цієї системи тілами, й зумовлена розташуванням тіл у просторі. Разом із кінетичною енергією, яка враховує не тільки положення тіл у просторі, а й рух, потенціальна енергія складає механічну енергію фізичної сиcтеми.

Потенціальна енергія матеріальної точки визначається як робота з її переміщення із точки простору, для якої визначається потенціальна енергія у якусь задану точку, потенціальна енергія якої приймається за нуль. Потенціальна енергія визначається лише для поля консервативних сил.

Потенціальна енергія здебільшого позначається літерами 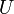або .

Залежність потенціальної енергії матеріальної точки від просторових координат утворює скалярне поле .

Сила, яка діє на частку в полі , визначається, як

Повна енергія матеріальної точ

Фізичні сили, для яких можна впровадити потенціальну енергію називаються потенціальними силами.

Значення потенціальної енегрії загалом визначене з точністю до певної сталої, водночас різниця значень потенціальної енергії частинки в різних положеннях — однозначна величина. Тому здебільшого рівень потенціальної енергії в якійсь певній точці чи при якомусь певному положенні вибирається за нульовий, а для інших точок чи положень системи потенціальна енергія відраховується від цього рівня.

11. Імпульсом або вектором кількості руху в класичній механіці називається міра механічного руху тіла, векторна величина, що для матеріальної точки дорівнює добутку маси точки на їїшвидкість та має напрямок швидкості.

В класичній механіці імпульс (традиційно позначається p) визначається як добуток маси тіла m та його швидкості v:

p = m v.

Мірою механічного руху, яка визначає можливість передачі механічного руху від одного тіла до іншого, є кількість руху або імпульс тіла Р. Імпульс тіла - це векторна фізична величина, напрям якої співпадає з напрямом швидкості v: Р=M*V. Повний імпульс системи тіл Р дорівнює векторний сумі імпульсів окремих тіл:

Імпульс сили — векторна фізична величина, яка дорівнює добутку сили на час її дії.

,

де — імпульс сили.

Приріст імпульсу тіла під дією сили , що діє впродовж часу дорівнює імпульсу сили.

.

Закон збереження імпульсу - один із фундаментальних законів фізики, який стверджує, що у замкненій системі сумарний імпульс усіх тіл зберігається.

Якщо на систему тіл зовнішні сили не діють або вони врівноважені, то така система називається замкненою, для неї виконується закон збереження імпульсу: повний імпульс замкненої системи тіл залишається незмінним за будь-яких взаємодій тіл цієї системи між собою:

Закон збереження імпульсу є наслідком однорідності простору.

12. Релятивістська механіка - розділ фізики, який розглядає закони механіки (закони руху тіл і часток) при швидкостях, порівнянних зі швидкістю світла. При швидкостях значно менших швидкості світла переходить в класичну (ньютонівську) механіку. Релятивістська механіка - теорія, в якій, на відміну від класичної механіки, де просторові координати і час є незалежними, при відсутності голономних зв'язків залежать від часу, (час є абсолютним, тобто тече однаково у всіх системах відліку) і діють перетворення Галілея, події відбуваються в чотиривимірному просторі, що об'єднує фізична тривимірний простір і час (простір Мінковського) і діють перетворення Лоренца. Таким чином, на відміну від класичної механіки, одночасність подій залежить від вибору системи відліку.

Основні закони релятивістської механіки - релятивістське узагальнення другого закону Ньютона і релятивістський закон збереження енергії-імпульсу є наслідком такого " змішування" просторових і тимчасової координат при перетвореннях Лоренца.

13. Зако́ н всесві́ тнього тяжі́ ння — фізичний закон, що описує гравітаційну взаємодію в рамках Ньютонівської механіки. Закон стверджує, щосила притягання між двома тілами (матеріальними точками) прямо пропорційна добутку їхніх мас, і обернено пропорційна квадрату відстані між ними.

Закон всесвітнього тяжіння сформулював Ісаак Ньютон у 1687 році у трактаті «Philosophiæ Naturalis Principia Mathematica».

У математичній формі закон всесвітнього тяжіння записується для матеріальних точок у вигляді:

,

де 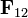— сила, що діє на друге тіло (матеріальну точку) з боку першого тіла, — гравітаційна стала, та — маси першого та другого тіла, відповідно, — вектор, що сполучає перше тіло з другим. — відстань між тілами.

14. Прискорення вільного падіння (позначення g) — прискорення, яке отримує тіло, рухаючись під впливом сили тяжіння Землі. Воно однакове для всіх тіл, залежить від географічноїшироти місцезнаходження тіла, його висоти підняття над рівнем моря та інших факторів.

Прискорення вільного падіння не залежить від маси тіл, але сильно змінюється в залежності від маси самої планети (і навіть від положення на ній, від полюса до екватора), див. таблицю значень g для інших небесних тіл.

Прискорення вільного падіння не однакове скрізь на Землі. Стандартне значення приблизно відповідає прискоренню падіння тіла на широті 45° і на висоті рівня моря. Відхилення від стандартної величини обумовлено низкою причин:

- Обертанням Землі. Внаслідок обертання Землі, за рахунок дії доцентрової сили, прискорення вільного падіння тіла на полюсах вище, ніж на екваторі.

- Формою Землі. Земля не ідеальна сфера, а має сплюснуту на полюсах форму.

- Висотою над рівнем моря.

- Неоднорідністю Землі.

15. Дія сили на тверде тіло залежить не тільки від модуля цієї сили, але і від площі поверхні тіла, на яку вона діє. Взаємодія рідин і газів із твердими тілами, а також взаємодія між сусідніми шарами рідини або газу теж відбувається не в окремих точках, а на певній поверхні їх дотикання. Одна і та ж людина глибоко провалюється, йдучи по снігу, і майже не провалюється у сніг, стаючи на лижі. Тому для характеристики подібних взаємодій введено поняття тиску.

Тиском p називають скалярну фізичну величину, що дорівнює відношенню модуля сили тиску, що діє перпендикулярно до поверхні, до площі цієї поверхні S:

У разі рівномірного розподілу сил тиску тиск на всіх ділянках поверхні однаковий і чисельно дорівнює силі тиску, що діє на поверхню одиничної площі.

Залежність тиску в рідині або газі від глибини приводить до виникнення виштовхувальної сили, що діє на будь-яке тіло, занурене в рідину або газ. Цю силу називають архімедовою силою. Дійсно, якщо тверде тіло занурюється в рідину або газ, то воно буде витісняти рідину (газ) і в результаті рідина (газ) чинитиме на тверде тіло тиск у відповідь. Цей приклад прояву третього закону Ньютона стверджує, що дія і протидія рівні та протилежні. Грецький учений Архімед за два століття до початку нашої ери встановив за допомогою дослідів, що виштовхувальна сила дорівнює вазі витісненої тілом рідини (F_A = mg = r₀ gV). Виведемо цю формулу. Для цього помістимо тіло у формі куба з ребром h та площею грані S у рідину густиною r_0.Отже, закон Архімеда формулюється так: на тіло, занурене в рідину або газ, діє виштовхувальна сила, що чисельно дорівнює вазі рідини або газу, витіснених зануреною частиною тіла, напрямлена вертикально вгору і прикладена в центрі тяжіння витісненого об'єму рідини або газу.

16. Рівня́ ння Берну́ ллі — рівняння гідроаеромеханіки, яке визначає зв'язок між швидкістю рідини, тиском в ній та висотою частинок над площиною відліку. Рівняння Бернуллі виражає закон збереження енергії рухомої рідини. Застосовується в гідравліці і гідродинаміці. Виведене Данилом Бернуллі в 1738 р.

Для виведення рівняння Бернуллі стосовно елементарної цівки в'язкої рідини розглянемо його енергетичний сенс. З цією метою підрахуємо механічну енергію нескінченно малої частки масою dm з центром у т. А, що знаходиться в межах елементарної цівки, щодо горизонтальної площини порівняння О1 – О1.

Як відомо, потенціальна енергія дорівнює:

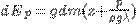
Отже, виходячи з вище сказаного кінцевий вигляд рівняння Бернуллі для елементарної струминки реальної рідини має вигляд:

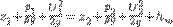
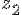де і - питомі енергії положення, що характеризують потенційну енергію в перерізах 1-1 і 2-2;

і - питомі енергії тиску, що характеризують потенційну енергію тиску в тих же перерізах;

і 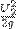- питомі кінетичні енергії у тих же перерізах;

- втрати питомої енергії.

17. Коливання — найпоширеніша форма руху в навколишньому світі та техніці.

Бачимо, що основною рисою коливань є їх періодичність. Але періодичними є й обертові рухи. На відміну від обертових рухів, які мають для кожної точки колові траєкторії, під час коливальних рухів точка чи тіло рухаються в протилежних напрямах по одній і тій самій траєкторії.У коливальному русі точка (тіло) проходить всі точки траєкторії руху (окрім двох крайніх) двічі — один раз в одному напрямі, другий - у зворотному.

Гармонічними коливаннями називаються періодичні коливання фізичної величини, які відбуваються згідно із законом

,

де 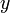— це фізична величина, що коливається, — час, — це найбільше значення, яке приймає величина 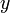під час коливань, яке називають амплітудою коливань, — циклічна частота коливань, — фаза коливань.

Періодом коливань називається величина

.

Лінійна частота коливань визначається, як

.

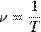18. Механічне коливання — такий вид руху тіла, під час якого воно багаторазово проходить одні й ті самі положення. Коливання називаються гармонічними, якщо їх характеристики (наприклад, зміщення тіла з положення рівноваги) змінюються у часі за законом синуса або косинуса.
Вільними (власними) називаються коливання, які здійснює тіло за рахунок початкової енергії, без зовнішньої дії під час коливань. Період — час одного коливання, , обернена величина — частота ; , (герц), .
Величина, аналогічна кутовій швидкості обертання , називається циклічною (круговою) частотою коливань: .
Амплітудою коливаньА називається максимальне зміщення матеріальної точки з положення рівноваги: .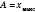

19. Гармонічними коливаннями називаються періодичні коливання фізичної величини, які відбуваються згідно із законом

,

де 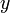— це фізична величина, що коливається, — час, — це найбільше значення, яке приймає величина 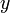під час коливань, яке називають амплітудою коливань, — циклічна частота коливань, — фаза коливань.

Періодом коливань називається величина

.

Лінійна частота коливань визначається, як

.

Розгляд гармонійних коливань важливо з двох причин:

Коливання зустрічаються в природі і техніці, часто мають характер, близький до гармонійному;