Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Разрыв одной фазы

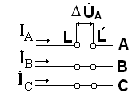
Разрыв одной фазы (рис.4.17) можно характеризовать следующими граничными условиями:

(4.57)

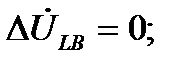(4.58)

(4.59)

Эти условия аналогичны граничным условиям двухфазного к.з. на землю, следовательно данная аналогия должна быть и в расчетных выражениях.

Так при разложении на симметричные составляющие условия (4.58)-(4.59) приводят к равенствам:

(4.60)

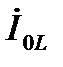Используя (4.55)-(4.56) и (4.60), выразим и через :

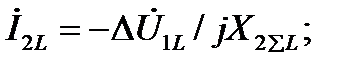(4.61)

(4.62)

В соответствии с (4.57) можно записать

,

откуда , (4.63)

где верхний индекс (1) и далее (2) одновременно с нижним индексом указывает обрыв соответственно одной и двух фаз.

После подстановки (4.63) в (4.54), получим:

. (4.64)

Подставляя (4.63) в (4.61)-(4.62), найдем:

; (4.65)

. (4.66)

Для определения напряжений с одной из сторон продольной несииметрии

(при разрыве одной фазы) нужно предварительно найти по схемам отдельных последовательностей симметричной части цепи соответствующие составляющие этих напряжений. Прибавив к ним 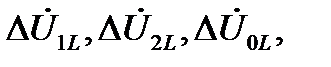получают симметричные составляющие напряжений с другой стороны продольной несимметрии.

Далее, зная все симметричные составляющие токов и напряжений, определяют фазные величины токов и напряжений путем сложения симметричных составляющих соответствующих фаз.

В частности, для определения фазных токов в месте обрыва одной фазы могут быть использованы выражения, аналогичные (4.32), в которых ток 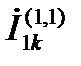и реактивност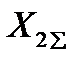и и должны быть соответственно замененены током и реактивностями и .

Аналогично, для нахождения модуля фазных токов при обрыве одной фазы может быть использован коэффициент, определяемый по выражению, аналогичному (4.33).

На рис. 4.18 в качестве иллюстрации приведены векторные диаграммы напряжений по концам разрыва (соответственно в точках и ), а на рис.4.19 – комплексная схема замещения.