Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Вказівки до виконання роботи. Для виконання роботи необхідно вивчити такий матеріал: явища переносу; теплопровідність.

Для виконання роботи необхідно вивчити такий матеріал: явища переносу; теплопровідність.

[ 1, т.1 §§ 15.3; 2, §§ 48; 3, вступ до розд.5, §§ 5.8–5.10; 4, т.1 §§ 112, 113]

Щоб експериментально визначити коефіцієнт теплопровідності l можна використати процес передачі теплоти в твердому тiлi, оскільки закономірності такого процесу завжди пов’язані з коефіцієнтом теплопровідності.

Коефіцієнт теплопровідності можна знайти з основного рівняння, яке описує процес теплопровідності – рівняння Фур’є:

,

де – кількість тепла, що передається вздовж осі x крізь елемент площі за час при градієнті температури .

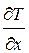Звiдси

.

Практичне вимірювання величин, які входять в останнє рівняння, має деякі ускладнення, тому краще розглядати такi процеси, в яких можна легко i точно вимiряти всi величини, що входять до розрахункової формули для визначення . Один iз таких процесiв – регулярний режим.

Нехай нагрiте до деякої температури T тiло розмiщене в середовищi, яке добре проводить тепло (наприклад вода).Температура цього середовища пiдтримується сталою і рівною T ₀. Тодi внаслiдок теплопровiдностi рiзниця температур тiла та середовища 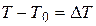постiйно зменшуватиметься i в момент встановлення рiвноваги дорiвнюватиме нулю. Закон цього зменшення, тобто функцiя Δ T = f (t), залежить вiд розмiрiв та форми тiла, його теплофiзичних властивостей, а також вiд того, як було нагрiте тiло (рiвномiрно чи нi) перед початком дослiду. В початковiй стадiї теплообмiну цей закон досить складний.

З часом настає так званий регулярний режим нагрiвання (чи охолодження), при якому рiзниця температур мiж будь-якою точкою зразка та навколишнiм середовищем залежить вiд часу за законом:

. (2.2.1)

Величина a у формулі (2.2.1) називається темпом нагрiвання (чи охолодження) i пов’язана з властивостями тiла:

, (2.2.2)

де k – коефiцiєнт форми, що залежить вiд форми та розмiрiв тiла; c – питома теплоємнiсть тiла; r – густина тiла. Для цилiндра:

, (2.2.3)

де R, h – вiдповiдно радiус i висота цилiндра.

Таким чином, визначення коефiцiєнта теплопровідностi l цилiндричного зразка з вiдомими густиною речовини r та питомою теплоємнiстю c зводиться до визначення темпу нагрiвання а. З цiєю метою вимiрюють рiзницю температур мiж зразком i зовнiшнiм середовищем у рiзнi моменти часу.

Згiдно з (2.2.1)

. (2.2.4)

Залежність після настання регулярного режиму на графіку має вигляд прямої з кутовим коефіцієнтом а (рис. 2.2.1).

Щоб знайти темп нагрівання а, на прямолiнiйнiй ділянці графіка вибирають довільно (але на досить великій відстані одна від одної) точки 1 i 2. Для цих точок визначають моменти часу τ ₁ та τ ₂, а також відповідні їм значення логарифмів різниці температур lnΔ T ₁ i lnΔ T ₂.

Тодi темп нагрівання розраховується за формулою:

. (2.2.5)

Пiсля визначення темпу нагрiвання можна знайти коефiцiєнт теплопровiдностi:

. (2.2.6)

За середовище, в якому нагрiвається зразок, доцiльно взяти воду, яка кипить, оскiльки, по-перше, в цьому разi забезпечується достатнiй теплообмiн поверхнi зразка з водою за рахунок перемiшування, по-друге, температура води, що кипить, вiдома та не змiнюється, коли зразок нагрiвається.

Температуру вимiрюють за допомогою диференцiальної термопари та потенцiометра постiйного струму або самозаписувача.