
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Введение. Физические основы электромагнетизма
|
|
Физические основы электромагнетизма
Часть 2
Магнитное поле и электромагнитная индукция
Учебное электронное издание
Владимир 2013
УДК 538.3
ББК 22.33
Г 65
Рецензент
Кандидат физико-математических наук, доцент кафедры технико-технологических дисциплин, декан технико-экономического факультета Владимирского государственного университета имени Александра Григорьевича и Николая Григорьевича Столетовых
В.А. Игонин
Соответствует требованиям государственных стандартов. Состоит из трёх глав, в которых раскрывается физический смысл основных законов и понятий электромагнетизма.
Предназначено для студентов второго и третьего курсов всех форм обучения и специальностей педагогического образования, изучающих физику.
Рекомендовано для формирования профессиональных компетенций в соответствии с ФГОС 3-го поколения.
Ил. 41. Библиогр.: 5 назв.
УДК 538.3
ББК 22.33
© ФГБОУ ВПО «Владимирский государственный университет», 2013
© Гончаров А.В., 2013
Введение
В первой части издания рассматривались вопросы, связанные с электростатическим полем и с постоянным электрическим током. Вторая часть посвящена раскрытию физического смысла основных законов постоянного магнитного поля, электромагнитной индукции и магнитных свойств вещества.
Особое внимание следует обратить на понятия поток и циркуляция вектора магнитной индукции, с помощью, которых формулируются основные законы и свойства магнитного поля. Законы Био-Савара-Лаплпса и закон полного тока позволяют решить основную задачу магнитостатики: рассчитать индукцию во всех точках магнитного поля по заданному распределению постоянных токов.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Приводятся примеры практического использования сил Ампера и Лоренца, а также эффекта Холла.
Подробно разбираются опыты Фарадея по электромагнитной индукции, которые привели к открытию вихревого электрического поля и созданию генераторов постоянного и переменного напряжения.
В последней главе описываются магнитные свойства вещества и методы расчёта магнитного поля в магнетиках.
Приводимые ссылки на веб-страницы, позволяют, познакомиться с работами А.Г.Столетова по намагничиванию железа.
В конце каждой главы для самостоятельной работы приводятся вопросы и качественные задачи, позволяющие оценить уровень усвоения теоретического материала.
Данное издание является дополнением к читаемому курсу лекций «Общая и экспериментальная физика» для студентов физико-математического факультета по направлению педагогическое образование.
Глава I. Основные магнитные явления. Законы магнитного поля
§ 1.1 Опыты Эрстеда и Ампера. Вектор магнитной индукции
Изучение магнитных явлений развивалось совершенно отдельно от исследований электричества, так как эти области казались совсем не связанными друг с другом. До некоторых пор считалось, что магнитными свойствами наделены, прежде всего, железо и каким-то образом сама Земля.
Но уже в начале XIX века было накоплено много интересных и удивительных фактов, таких как размагничивание или перемагничивание корабельных компасов и намагничивание металлических изделий во время грозы. Эти факты были описаны и систематизированы французским учёным Ф. Араго. К тому времени некоторые учёные (Эрстед, Ампер, Араго) исходя из взаимосвязи явлений в природе, полагали, что между электрическими и магнитными явлениями существует определённая связь.
В 1820 г Ганс (Ханс) Кристиан Эрстед сделал открытие (во время чтения лекции студентам), что электрический ток влияет на магнитную стрелку компаса.
Опыт Эрстеда изображён на рис.
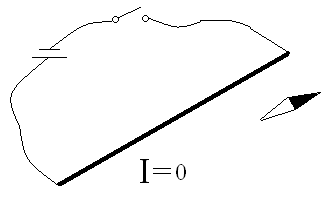

Рис.1
а) до замыкания цепи б) после замыкания цепи
В момент замыкания цепи проводник с током действует на стрелку, поворачивая её на 900.
В том же году Ампер обнаружил наличие сил, действующих между двумя проводами с током. На рис.2 представлены опыты Ампера. Если ток в проводах течёт в одном направлении, то провода притягиваются друг к другу с силами равными по величине  (рис.2а). В случае противоположного направления токов, провода отталкиваются (рис.2б). Силы
(рис.2а). В случае противоположного направления токов, провода отталкиваются (рис.2б). Силы  и
и  не являются электрическими т.к. провода с током электрически нейтральны.
не являются электрическими т.к. провода с током электрически нейтральны.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе

Рис.2
а) б)
Стало очевидным, что электрические токи могут производить магнитные эффекты, и в свою очередь магниты могут вызывать силы, действующие на токи. Такие силы Ампер назвал магнитными.
Для описания электростатических взаимодействий было введено понятие электростатическое поле, аналогично механизм магнитных взаимодействий можно описать с помощью магнитного поля.
Магнитное поле создаётся вокруг проводника с током и распространяется в пространстве с конечной скоростью (3·108 м/с) и действует с некоторой силой на магнитную стрелку или проводник с током. Учитывая, что электрический ток – это направленное движение заряженных частиц, можно сделать вывод, что источником магнитного поля являются движущиеся электрически заряженные частицы.
Магнитное поле в пространстве можно обнаружить по его основному свойству: поле действует с некоторой силой на проводник с током или движущуюся электрически заряженную частицу или магнитную стрелку. На неподвижные электрические заряды магнитное поле не действует.
Таким образом, магнитное поле можно изучать с помощью магнитной стрелки или рамки с током.
На рамку с током в магнитном поле будет действовать пара сил, создающая вращательный момент, и рамка начнёт поворачиваться (рис.3).
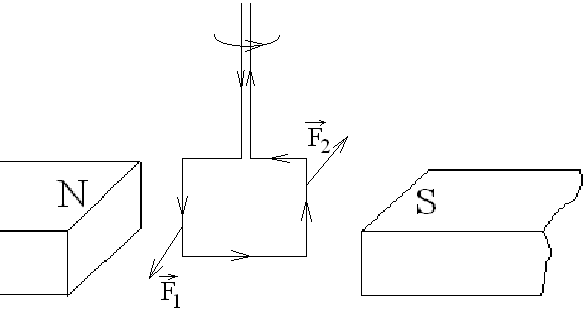
Рис.3
Эта маленькая рамка с током играет роль пробного заряда, который использовался для изучения электрического поля.
Ток в рамке должен быть малым, чтобы не искажать исследуемое магнитное поле. Эксперимент показывает, что максимальный момент 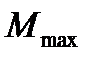 , действующий на рамку пропорционален силе тока
, действующий на рамку пропорционален силе тока  в рамке и её площади
в рамке и её площади  :
:  ~
~ 
Отношение 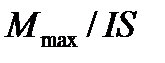 не зависит от свойств рамки и характеризует магнитное поле в данной точке. Произведение
не зависит от свойств рамки и характеризует магнитное поле в данной точке. Произведение  называют магнитным моментом рамки:
называют магнитным моментом рамки:  .
.
Магнитный момент является векторной величиной  , направление которой определяется по правилу правого буравчика: если ручку буравчика вращать по направлению тока, то поступательное движение буравчика совпадает с направлением вектора
, направление которой определяется по правилу правого буравчика: если ручку буравчика вращать по направлению тока, то поступательное движение буравчика совпадает с направлением вектора  . Вектор
. Вектор  направлен по нормали к рамке.
направлен по нормали к рамке.
Опыты показывают, что отношение  не зависит от силы тока в рамке в данной точке магнитного поля. Это отношение есть численное значение вектора магнитной индукции
не зависит от силы тока в рамке в данной точке магнитного поля. Это отношение есть численное значение вектора магнитной индукции 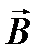 поля, и является его силовой характеристикой:
поля, и является его силовой характеристикой:  .
.
Направление вектора 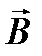 в данной точке магнитного поля можно определить с помощью рамки с током или магнитной стрелки. Условились считать, что вектор
в данной точке магнитного поля можно определить с помощью рамки с током или магнитной стрелки. Условились считать, что вектор  рамки с током указывает направление вектора
рамки с током указывает направление вектора  , если рамка находится в устойчивом равновесии (рис.4). Во втором случае за направление вектора
, если рамка находится в устойчивом равновесии (рис.4). Во втором случае за направление вектора  принимается направление от южного полюса (S) к северному (N) магнитной стрелки, свободно устанавливающейся в магнитном поле (рис.4).
принимается направление от южного полюса (S) к северному (N) магнитной стрелки, свободно устанавливающейся в магнитном поле (рис.4).

Рис.4
Графически магнитное поле можно представить в виде силовых линий или линиями магнитной индукции – линиями, касательные к которым совпадают с вектором 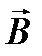 в каждой точке. Из опытов известно, что линии магнитной индукции всегда замкнуты и охватывают проводники с током (рис.5).
в каждой точке. Из опытов известно, что линии магнитной индукции всегда замкнуты и охватывают проводники с током (рис.5).
| поле прямого тока |
| поле кругового тока |
| поле соленоидального тока |


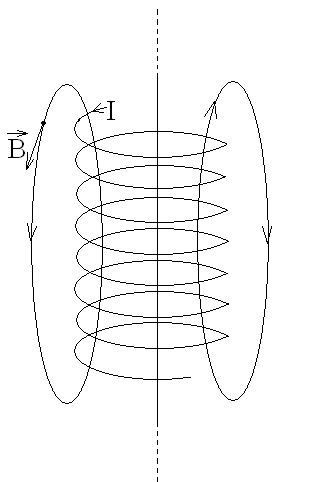
Рис. 5
Таким образом, поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:
 .
.
Это означает, что в природе не существует магнитных зарядов.
Направление силовых линий определяется по правилу правого буравчика.
Магнитное поле, созданное током, зависит от силы тока, формы проводника и среды, которая окружает проводник. Отношение индукции 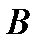 в среде к индукции поля в вакууме
в среде к индукции поля в вакууме 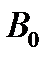 характеризует магнитные свойства среды
характеризует магнитные свойства среды 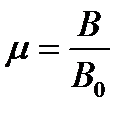 ,
,  - магнитная проницаемость среды.
- магнитная проницаемость среды.
В ряде случаев для расчёта магнитных полей используют понятие напряжённости магнитного поля  . Между векторами
. Между векторами  и
и  существует связь:
существует связь:
 , (1.1)
, (1.1)
где  - магнитная постоянная (
- магнитная постоянная (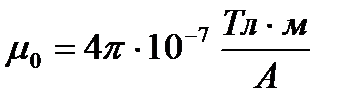 ), µ - магнитная проницаемость вещества.
), µ - магнитная проницаемость вещества.
Магнитное поле, также как и электростатическое подчиняется принципу суперпозиции,
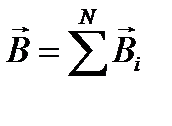 ,
,
где  - магнитная индукция поля, создаваемая i -мисточником.
- магнитная индукция поля, создаваемая i -мисточником.
§1. 2. Закон Био-Савара-Лапласа
Одной из основных функций электромагнетизма является расчёт магнитных полей по заданным токам. Для её решения может быть использован закон Био-Савара-Лапласа. Согласно которого, элемент тока  создаёт в любой точке вакуума (рис.6) магнитную индукцию
создаёт в любой точке вакуума (рис.6) магнитную индукцию  , определяемую по формуле (1.2):
, определяемую по формуле (1.2):
 или
или  (1.2)
(1.2)

Рис.6.
Используя принцип суперпозиции, полная индукция в точке А находится суммированием выражений (2.1) по всем элементам тока данного замкнутого контура.
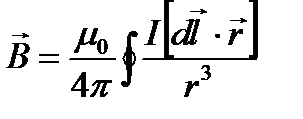 . (1.3)
. (1.3)
Учитывая, что электрический ток – это направленное движение электрических зарядов ( ), из формулы (1.1) можно рассчитать индукцию, создаваемую в т. А одним зарядом, движущимся со скоростью
), из формулы (1.1) можно рассчитать индукцию, создаваемую в т. А одним зарядом, движущимся со скоростью 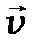 (рис.7):
(рис.7):
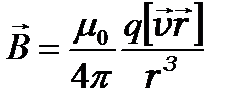 (1.4) или
(1.4) или  (1.5)
(1.5)

Рис.7
§1.3. Магнитное поле кругового и прямолинейного токов
Воспользуемся законом Био-Савара-Лапласа для расчёта магнитных полей создаваемых круговым и прямым токами.
Рассмотрим в вакууме круговой контур (рис.8) с радиусом R, по которому проходит ток силой  . Необходимо определить индукцию
. Необходимо определить индукцию  в центре контура (в точке С) и на оси контура (в точке А).
в центре контура (в точке С) и на оси контура (в точке А).

Рис.8 Магнитное поле в центре и на оси кругового тока
Направление индукции в точке С определяется по правилу правого буравчика. Согласно (1.3), и учитывая, что все элементы тока  перпендикулярны к радиус-вектору
перпендикулярны к радиус-вектору 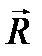 (
( ), можно записать для
), можно записать для  :
:
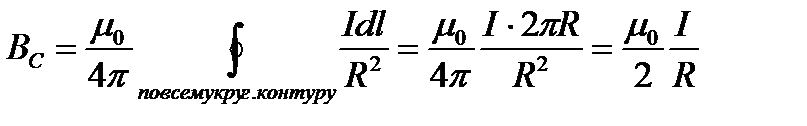 . (1.6)
. (1.6)
В точке А два симметричных элемента тока 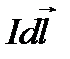 создают симметрично расположенные индукции
создают симметрично расположенные индукции  (рис.8), векторная сумма которых направлена по оси контура. Модуль результирующего вектора
(рис.8), векторная сумма которых направлена по оси контура. Модуль результирующего вектора 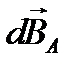 , с учётом того, что угол α между векторами
, с учётом того, что угол α между векторами 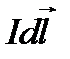 и
и  составляет 900, равен:
составляет 900, равен:
 .
.
Используя формулу (1.3), получим
 (1.7) или
(1.7) или 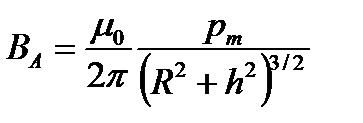 (1.8),
(1.8),
где  - магнитный момент кругового тока. Из (1.7 и 1.8) следует, что при
- магнитный момент кругового тока. Из (1.7 и 1.8) следует, что при  индукция обратно пропорциональна третьей степени
индукция обратно пропорциональна третьей степени  . Магнитное поле на оси кругового тока имеет ту же самую функциональную зависимость от расстояния, что и электрическое поле, создаваемое электрическим диполем
. Магнитное поле на оси кругового тока имеет ту же самую функциональную зависимость от расстояния, что и электрическое поле, создаваемое электрическим диполем  .
.
Найдём магнитную индукцию, создаваемую прямолинейным током (рис.9).
| б) конечной длины |
| а) бесконечной длины |
| а) бесконечной длины |

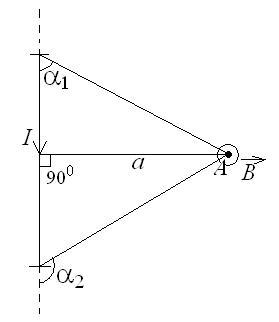
Рис.9.
В данном случае направление индукции всех элементов тока  в точке А одинаково и перпендикулярно плоскости чертежа. Поэтому можно складывать модули векторов
в точке А одинаково и перпендикулярно плоскости чертежа. Поэтому можно складывать модули векторов 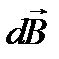 . Индукция, создаваемая элементом тока, выражается формулой (1.2):
. Индукция, создаваемая элементом тока, выражается формулой (1.2): 
Из рис.9 видно, что  ,
,  .
.
Подставляя эти выражения в (1.2), получим  .
.
В случае бесконечно длинного проводника или l > > a, находим:
 . (2.9)
. (2.9)
При конечной длине провода:
 (2.10)
(2.10)
§1.4. Закон полного тока
Для расчёта магнитных полей в определённых случаях используют закон полного тока (или закон Ампера). Он играет такую же важную роль, как и теорема Остроградского-Гаусса в электростатике.
Рассмотрим ток, текущий по прямолинейному бесконечному проводнику, и вычислим циркуляцию вектора  по замкнутому вокруг тока
по замкнутому вокруг тока  контуру L, лежащему в плоскости, перпендикулярной проводнику (рис.10):
контуру L, лежащему в плоскости, перпендикулярной проводнику (рис.10):
 . (2.11)
. (2.11)
| в)объёмные токи |
| б)контур не охватывает ток |
| а)контур охватывает ток |


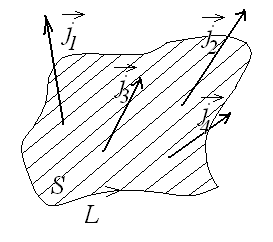
Рис.10. К вычислению циркуляции вектора  .
.
При вычислении интеграла (1.11), используя формулу (1.9) и обозначения, показанные на рис.10, получим  ,
, 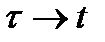 ,
,
но 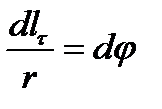 , поэтому (1.11) можно переписать в виде
, поэтому (1.11) можно переписать в виде
 (1.12)
(1.12)
Следовательно, циркуляция вектора  по замкнутому контуру вокруг тока не зависит от формы контура и определяется только силой тока.
по замкнутому контуру вокруг тока не зависит от формы контура и определяется только силой тока.
Если замкнутый контур  не охватывает ток
не охватывает ток  (рис.10, б), то при обходе такого контура по направлении
(рис.10, б), то при обходе такого контура по направлении  , например, начиная от точки 1 до точки 2, угол φ возрастёт. При продолжении обхода, начиная с точки 2 до точки 1, угол φ – уменьшается. Поэтому
, например, начиная от точки 1 до точки 2, угол φ возрастёт. При продолжении обхода, начиная с точки 2 до точки 1, угол φ – уменьшается. Поэтому  . Таким образом, циркуляция вектора
. Таким образом, циркуляция вектора  по замкнутому контуру, не охватывающему ток, равна нулю.
по замкнутому контуру, не охватывающему ток, равна нулю.
Полученные результаты имеют общий характер, не зависимый от формы токов и количества токов, охватываемых контуром, и выражают закон полного тока: циркуляция вектора магнитной индукции по любому замкнутому контуру равна произведению 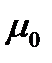 на алгебраическую сумму токов, охватываемых данным контуром:
на алгебраическую сумму токов, охватываемых данным контуром:
 . (1.13).
. (1.13).
В формуле (2.13) знак тока  определяется по общему правилу: если направление обхода контура L и направление тока связаны правилом правого буравчика, то знак
определяется по общему правилу: если направление обхода контура L и направление тока связаны правилом правого буравчика, то знак  положителен, в противном случае знак I отрицателен.
положителен, в противном случае знак I отрицателен.
В общем случае распределение постоянного тока задаётся плотностью тока  . Рассмотрим контур L (рис.10 в), охватывающий токи. Полный ток, охватываемый контуром L, равен потоку вектора
. Рассмотрим контур L (рис.10 в), охватывающий токи. Полный ток, охватываемый контуром L, равен потоку вектора  через поверхность, опирающуюся на данный контур;
через поверхность, опирающуюся на данный контур;
 . (1.14)
. (1.14)
Следовательно, запись закона полного тока можно представить в виде:
 . (1.15)
. (1.15)
§1.5. Магнитное поле соленоида и тороида
Соленоид представляет собой большое число витков с током, навитых непрерывно на цилиндр. На рис.11 приводится сечение соленоида.

Рис.11.
Внутри соленоида магнитное поле однородно. Вблизи концов соленоида линии магнитной индукции расходятся и поле ослабевает. Из опытов известно, что при большой длине соленоида по сравнению с диаметром, магнитным полем вне соленоида можно пренебречь по сравнению с полем внутри. Используя данный факт и закон полного тока, можно вычислить поле внутри соленоида.
Рассчитаем циркуляцию вектора  по прямоугольному контуру abcda (рис.11). На участках контура bc и da произведение
по прямоугольному контуру abcda (рис.11). На участках контура bc и da произведение  , т.к. вектор
, т.к. вектор  перпендикулярен длинным отрезкам. На участке cd полем
перпендикулярен длинным отрезкам. На участке cd полем  . Поэтому,
. Поэтому,
 (1.16)
(1.16)
Согласно закону полного тока:
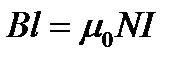 , (1.17)
, (1.17)
где N-число витков соленоида на длине l. Обозначив через  - число витков на единицу длины соленоида, получим
- число витков на единицу длины соленоида, получим
 . (1.18)
. (1.18)
Как следует из (2.18), поле внутри соленоида не зависит от полного числа витков, а только от числа витков на единицу длины и силы тока.
Вычислим магнитную индукцию тороидальной катушки с током (рис.12).

Рис.12.
Из соображений симметрии следует, что величина B одинакова во всех точках окружности, проходящей через центры витков катушки. Циркуляция вектора  по такой окружности с учётом закона полного тока равна
по такой окружности с учётом закона полного тока равна  , (1.19)
, (1.19)
где N – полное число витков катушки. Введя обозначение  - число витков на единицу длины, получим
- число витков на единицу длины, получим
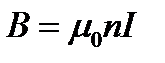 . (1.20)
. (1.20)
§1.6. Сила Ампера. Работа в магнитном поле
Из приведённых опытов Ампера (§1) следует, что на проводник с током, помещённым в магнитное, поле действует сила, которую называют силой Ампера. Опыты показывают, что сила Ампера пропорциональна элементу тока  , магнитной индукции B в окрестностях данного элемента и синуса угла (sinα) между векторами
, магнитной индукции B в окрестностях данного элемента и синуса угла (sinα) между векторами  и
и  (рис.13):
(рис.13):
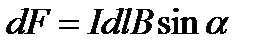 (1.21) или
(1.21) или  (1.22)
(1.22)
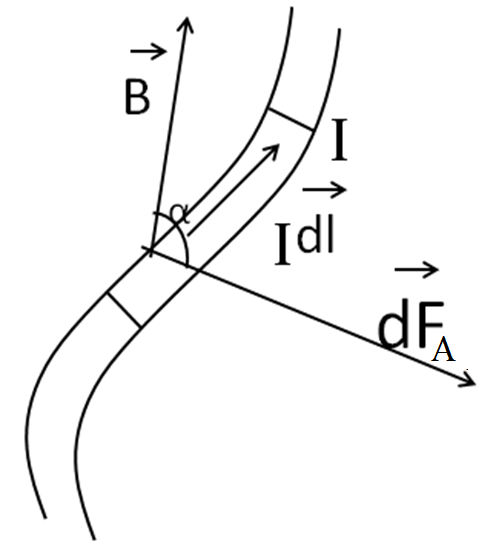
Рис.13.
Если прямолинейный отрезок проводника находится в однородном магнитном поле, то из формулы (1.22) имеем 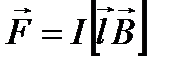 . (1.23)
. (1.23)
Направление силы Ампера перпендикулярно к  и
и 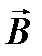 и определяется по правилу правого буравчика или по правилу левой руки: если левую руку расположить так, чтобы нормальная к проводнику составляющая вектора
и определяется по правилу правого буравчика или по правилу левой руки: если левую руку расположить так, чтобы нормальная к проводнику составляющая вектора  входила в ладонь, и четыре вытянутых пальца были направлены по направлению тока (
входила в ладонь, и четыре вытянутых пальца были направлены по направлению тока ( ), то отогнутый на 900 большой палец покажет направление силы Ампера.
), то отогнутый на 900 большой палец покажет направление силы Ампера.
Если проводник с током под действием силы Ампера передвигается, то совершатся определённая работа. Для вычисления этой работы рассмотрим однородное магнитное поле  , в котором находится контур с подвижной стороной длиной l (рис.14).
, в котором находится контур с подвижной стороной длиной l (рис.14).

Рис.14.
Согласно (1.23) на проводник l действует сила, равная 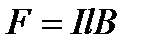 . Под действием этой силы за некоторый промежуток времени проводник l из первого положения сместится во второе, пройдя путь dx, элементарная работа этой силы равна
. Под действием этой силы за некоторый промежуток времени проводник l из первого положения сместится во второе, пройдя путь dx, элементарная работа этой силы равна
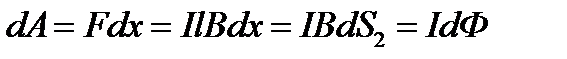 , (1.24)
, (1.24)
где dS-площадь, описанная проводником l при движении,
 - элементарный магнитный поток через элементарную площадку dS.
- элементарный магнитный поток через элементарную площадку dS.
Если перемещение проводника, конечно, то работа равна
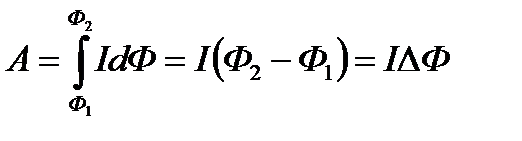 , (1.25)
, (1.25)
где Ф1-магнитный поток через контур в начале перемещения, Ф2-магнитный поток через контур в конце перемещения. При этом считается, что сила тока в проводнике l при его перемещении остаётся постоянной. В СИ за единицу магнитного потока принимается один вебер (Вб): 1 Вб =1 Тл·1 м2 = 1 Дж/А = 1 В·с. Отметим, что формула (1.24) справедлива и для вращательного движения проводника с током в магнитном поле.
§1.7. Контур с током в магнитном поле
Рассмотрим прямоугольный контур площадью S с током в однородном магнитном поле. Пусть сначала магнитный момент контура 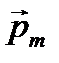 перпендикулярен линиям магнитной индукции (рис.15).
перпендикулярен линиям магнитной индукции (рис.15).

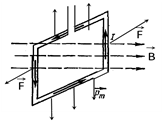
а) б)
Рис.15
а) плоскость контура параллельна линиям магнитной индукции
б) плоскость контура перпендикулярна магнитной индукции
В этом случае на стороны а действуют силы Ампера  , стремящиеся повернуть контур так, чтобы его магнитный момент
, стремящиеся повернуть контур так, чтобы его магнитный момент 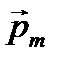 совпал с направлением линий индукции
совпал с направлением линий индукции  . Таким образом, на контур действует пара сил
. Таким образом, на контур действует пара сил  с некоторым вращательным моментом М. Предположим, что под действием этого момента контур поворачивается на элементарный угол dα, тогда работа сил Ампера будет равна
с некоторым вращательным моментом М. Предположим, что под действием этого момента контур поворачивается на элементарный угол dα, тогда работа сил Ампера будет равна
dA=Mdα. (1.26).
Эту работу можно рассчитать и по формуле (1.24), поэтому Mdα =IdФ, где dФ=BSsinα dα (Ф=BScosα), тогда Mdα =ISBsinα dα, откуда M=pmBsinα. (1.27).
Уравнение (1.27) можно представить в векторной форме
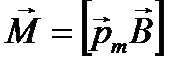 . (1.28).
. (1.28).
Полученный результат не зависит от формы контура и формула (1.28) справедлива не только для прямоугольного контура, но и для контура произвольной формы.
В однородном магнитном поле контур с током под действием вращательного момента  будет поворачиваться до тех пор, пока не займёт положение устойчивого равновесия. При этом на стороны контура будут действовать силы, стремящиеся разорвать контур. В этом случае вращательный момент
будет поворачиваться до тех пор, пока не займёт положение устойчивого равновесия. При этом на стороны контура будут действовать силы, стремящиеся разорвать контур. В этом случае вращательный момент  и вектора
и вектора  и
и  становятся сонаправленными.
становятся сонаправленными.
Рассмотрим неоднородное магнитное поле, в котором контур уже повернулся так, что линии магнитной индукции симметричны относительно вектора магнитного момента контура (рис.16).

Рис.16.
Из рис.16 видно, что горизонтальные составляющие 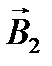 векторов
векторов  вызывают появление сил
вызывают появление сил  растягивающих контур, и составляющие
растягивающих контур, и составляющие  - к появлению сил
- к появлению сил 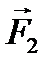 , стремящихся перемещать контур в область более сильного поля. Если вектор
, стремящихся перемещать контур в область более сильного поля. Если вектор  антипараллелен вектору
антипараллелен вектору  , то контур будет выталкиваться в область более слабого поля.
, то контур будет выталкиваться в область более слабого поля.
Силу, действующую в этом случае на контур, можно определить обычным приёмом. Предположим, что контур перемещается в направлении оси х на элементарный отрезок dx. При этом измениние магнитного потока через контур площадью S составит:  , а в то же время сила F совершит работу
, а в то же время сила F совершит работу
 .
.
Следовательно, сила F, действующая на контур равна
 , (1.29)
, (1.29)
т.е. сила пропорциональна быстроте изменения магнитной индукции в рассматриваемом направлении.
§8 Сила Лоренца. Движение заряженных частиц в магнитном
поле
На заряженную частицу, движущуюся с некоторой скоростью  в электрическом и магнитном поле, действует сила:
в электрическом и магнитном поле, действует сила:
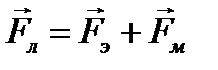 . (1.30)
. (1.30)
Эта сила  называется силой Лоренца. Она состоит из двух составляющих электрической
называется силой Лоренца. Она состоит из двух составляющих электрической 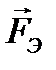 и магнитной
и магнитной  сил. Сила, действующая на заряд q со стороны электрического поля
сил. Сила, действующая на заряд q со стороны электрического поля  равна
равна
 . (1.31)
. (1.31)
Магнитную составляющую  определим из силы Ампера (1.22):
определим из силы Ампера (1.22):
 . Эту силу можно рассматривать как результирующую магнитных сил
. Эту силу можно рассматривать как результирующую магнитных сил  , действующих со стороны магнитного поля на движущиеся электрические заряды в элементарном объёме проводника dV.
, действующих со стороны магнитного поля на движущиеся электрические заряды в элементарном объёме проводника dV.
 , где n-концентрация свободных зарядов, dV=Sdl (S -площадь поперечного сечения проводника).
, где n-концентрация свободных зарядов, dV=Sdl (S -площадь поперечного сечения проводника).
Сила тока при средней скорости упорядоченного движения зарядов  , равна
, равна  , где S -поперечное сечение проводника.
, где S -поперечное сечение проводника.
Учитывая, что векторы q 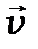 и Id
и Id  сонаправлены, сила Ампера принимает вид
сонаправлены, сила Ампера принимает вид
 ,
,
где dN -число зарядов в элементарном объёме проводника dV=Sdl. Силу Ампера можно рассматривать как результирующую магнитных сил  , действующих со стороны магнитного поля на движущиеся заряды в объёме проводника dV:
, действующих со стороны магнитного поля на движущиеся заряды в объёме проводника dV:  .
.
Поэтому, сила  , действующая на движущийся заряд в магнитном поле, равна
, действующая на движущийся заряд в магнитном поле, равна
 . (1.32)
. (1.32)
Таким образом, полная сила Лоренца равна
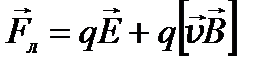 . (1.33)
. (1.33)
Направление магнитной составляющей силы Лоренца определяют по правилу левой руки (рис.17).
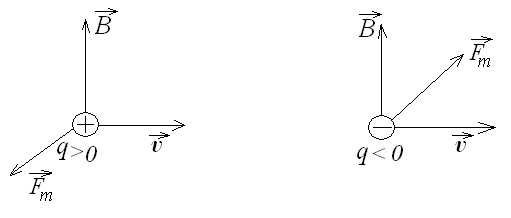
Рис.17. Сила, действующая на движущийся положительный и отрицательный электрические заряды.
Так как  перпендикулярна к скорости частицы, то она работы не совершает и не изменяет кинетическую энергию частицы.
перпендикулярна к скорости частицы, то она работы не совершает и не изменяет кинетическую энергию частицы.
Предположим, что в однородное магнитное поле с индукцией 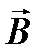 влетает положительно заряженная частица с начальной скоростью
влетает положительно заряженная частица с начальной скоростью  , перпендикулярной линиям индукции (рис.18). На частицу будет действовать сила Лоренца, равная магнитной составляющей:
, перпендикулярной линиям индукции (рис.18). На частицу будет действовать сила Лоренца, равная магнитной составляющей:  .
.
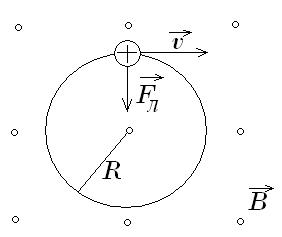
Рис.18.
Под действием этой силы частица будет двигаться по окружности радиусом R с постоянной по модулю скоростью  и центростремительным ускорением
и центростремительным ускорением  . По второму закону Ньютона
. По второму закону Ньютона  , отсюда
, отсюда
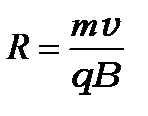 , (1.34)
, (1.34)
т.е. радиус окружности тем меньше, чем больше индукция.
Данное движение обладает важной особенностью: циклическая частота обращения не зависит от энергии частицы. Действительно, частота обращения равна
 , (1.35)
, (1.35)
где 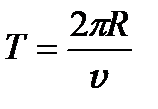 - период обращения, учитывая (1.34), можно записать
- период обращения, учитывая (1.34), можно записать
 . (1.36)
. (1.36)
Подставляя в (1.35) вместо Т его выражение (1.36), получим
 . (1.37)
. (1.37)
Эта частота называется циклотронной и для данного рода частиц зависит только от магнитной индукции.
Предположим, что положительно заряженная частица влетает со скоростью  в однородное магнитное поле под углом α к линиям индукции (рис.19).
в однородное магнитное поле под углом α к линиям индукции (рис.19).

Рис.19.
В этом случае скорость  можно разложить на нормальную составляющую
можно разложить на нормальную составляющую  и составляющую вдоль линий индукции
и составляющую вдоль линий индукции 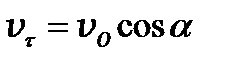 . На частицу будет действовать магнитная составляющая силы Лоренца, обусловленная составляющей
. На частицу будет действовать магнитная составляющая силы Лоренца, обусловленная составляющей 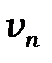 . Эта сила заставляет частицу двигаться по окружности. С другой стороны, составляющая
. Эта сила заставляет частицу двигаться по окружности. С другой стороны, составляющая  не вызывает появление дополнительной силы. Поэтому частица в направлении индукции движется равномерно. Благодаря сложению обоих движений частица будет двигаться по цилиндрической спирали (винтовой линии) (рис.19). Шаг винта данной спирали
не вызывает появление дополнительной силы. Поэтому частица в направлении индукции движется равномерно. Благодаря сложению обоих движений частица будет двигаться по цилиндрической спирали (винтовой линии) (рис.19). Шаг винта данной спирали  , подставляя вместо Т его выражение (1.36), получим
, подставляя вместо Т его выражение (1.36), получим
 . (1.38)
. (1.38)
§1.9. Циклотрон
Для изучения строения атомного ядра, искусственного превращения элементов и открытия новых элементарных частиц необходимо создание мощных ускорителей заряженных частиц. Первые ускорители состояли из двух основных частей – устройства для получения высокого напряжения и высоковольтной вакуумной трубки, внутри которой частицы движутся приблизительно по прямолинейным траекториям и ускоряются за счёт электрического поля. Такие ускорители назвали линейными.
Американский физик Лоуренс в тридцатых годах предложил идею: заставить ускоряемые частицы двигаться не по прямолинейным траекториям, а по круговым. Преимущество такого способа ускорения заключается в том, что отпадает необходимость в длинных ускорительных трубках и в больших напряжениях.
Как мы видели в §1. 8, заряженные частицы в однородном магнитном поле под действием силы Лоренца могут двигаться по окружности с частотой (1.37), не зависящей от радиуса траектории. Именно это обстоятельство позволило создать циклический ускоритель – циклотрон, в котором для ускорения частиц используется высокочастотное электрическое поле.
Устройство циклотрона представлено на рис.20: А – вакуумная камера, которая помещена между полюсами электромагнита; M и N -

Рис.20.
металлические дуанты. К ним с помощью электродов m и n от электрического генератора подаётся переменное напряжение  с циклотронной частотой
с циклотронной частотой  , определяемой по формуле (1.37).
, определяемой по формуле (1.37).
В центре промежутка между дуантами расположен источник С положительно заряженных частиц (протонов или ионов). Ион, вылетевший из источника в то время, когда электрод М (рис.20) имеет максимальный отрицательный потенциал, под действием электрического поля ускоряется в промежутке между дуантами и попадает в полость дуанта. Внутри дуанта ион под действием магнитного поля (силы Лоренца) описывает полуокружность постоянного радиуса, так как в полости дуанта электрическое поле отсутствует. При заданной циклотронной частоте к моменту выхода иона из полости М направление электрического поля изменится на противоположное. Поэтому ион вновь ускорится и внутри полости дуанта N опишет полуокружность большего радиуса.
Таким образом, двигаясь в резонансе с высокочастотным электрическим полем, ионы будут по раскручивающейся спирали двигаться к краю полюса магнита. Их энергия будет расти после каждого прохождения промежутка между дуантами на величину, равную  . Процесс ускорения продолжается до тех пор, пока частицы не достигнут края полюсов магнита, при этом пучок ускоренных частиц выводят из камеры посредством отклоняющего электрода. Под действием электрического поля, создаваемого данным электродом, пучок ускоренных ионов изменяет свою траекторию и попадают на мишень.
. Процесс ускорения продолжается до тех пор, пока частицы не достигнут края полюсов магнита, при этом пучок ускоренных частиц выводят из камеры посредством отклоняющего электрода. Под действием электрического поля, создаваемого данным электродом, пучок ускоренных ионов изменяет свою траекторию и попадают на мишень.
В типичном циклотроне при ускоряющих потенциалах порядка несколько десятков киловольт достигаются энергии частиц до десятков мегаэлектронвольт.
§ 1.10. Масс-спектрограф
Сила Лоренца также играет важную роль в приборе, называемом масс-спектрографом. Данный прибор позволяет определить удельные заряды и массы ионов. В масс-спектрографе используются комбинации статических электрических и магнитных полей. Впервые такой прибор был построен Астоном в 1917 г. Прибор Астона (рис.21) содержит все основные элементы современного масс-спектрографа. В этом приборе пучок положительных ионов, вышедших из ионного источника О, проходит две узкие щели S1 и S2 и попадает в электростатическое поле конденсатора К. Предположим сначала, что пучок состоит из одинаковых ионов, которые, следовательно, имеют один и тот же удельный заряд q/m и одну и ту же массу m.Скорости этих ионов, в общем случае, различны. Поэтому электрическое поле по-разному будет отклонять ионы, проходящие через конденсатор (К). Ионы с большей скоростью будут отклоняться меньше, чем ионы с меньшей скоростью.
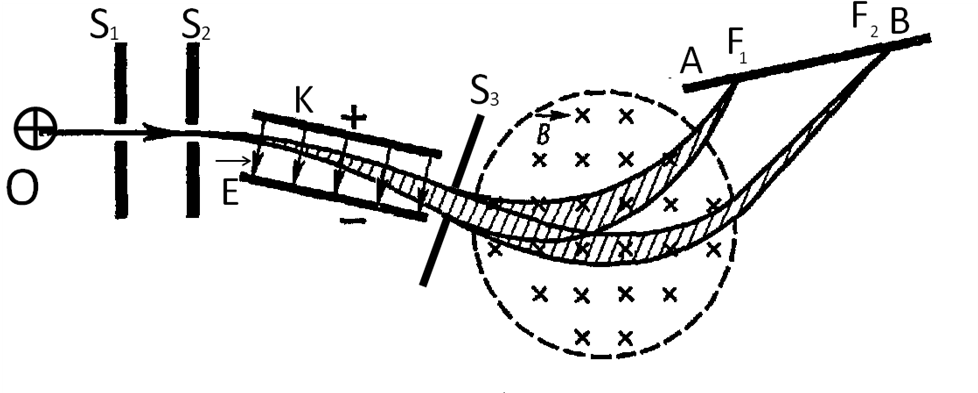
Рис21. Схема масс-спектрометра.
Таким образом, после конденсатора имеется расходящийся пучок ионов, часть которого проходит через диафрагму S3 в однородное магнитное поле  , имеющее направление перпендикулярное силовым линиям электростатического поля
, имеющее направление перпендикулярное силовым линиям электростатического поля 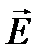 . В магнитном поле сила Лоренца сильнее отклоняет ионы с малой скоростью, чем с большей. Поэтому расходящийся пучок становится сходящимся и фокусируется в точке F1. Если в пучке положительных ионов находятся ионы с различными q/m и m, то ионы каждого сорта, имеющие одно и то же значение q/m и m, фокусируются в точках, расположенных вдоль линии АВ, куда помещается фотографическая пластина. На пластинке получится ряд узких линий, соответствующих различным значениям удельных зарядов ионов. Так как в магнитном поле
. В магнитном поле сила Лоренца сильнее отклоняет ионы с малой скоростью, чем с большей. Поэтому расходящийся пучок становится сходящимся и фокусируется в точке F1. Если в пучке положительных ионов находятся ионы с различными q/m и m, то ионы каждого сорта, имеющие одно и то же значение q/m и m, фокусируются в точках, расположенных вдоль линии АВ, куда помещается фотографическая пластина. На пластинке получится ряд узких линий, соответствующих различным значениям удельных зарядов ионов. Так как в магнитном поле  ионы движутся по дуге окружности, радиус которой определяется по формуле (1.34), то точка F1 соответствует ионам с большим удельным зарядом или меньшей массой, и точка F2 – ионам с большей массой. Если знать их удельный заряд ионов и их массу, дающих линию F1, расстояние между линиями F1 и F2 и параметры прибора, можно определить массу ионов, соответствующих линии F2.
ионы движутся по дуге окружности, радиус которой определяется по формуле (1.34), то точка F1 соответствует ионам с большим удельным зарядом или меньшей массой, и точка F2 – ионам с большей массой. Если знать их удельный заряд ионов и их массу, дающих линию F1, расстояние между линиями F1 и F2 и параметры прибора, можно определить массу ионов, соответствующих линии F2.
С помощью этого прибора Астон впервые измерил массы отдельных ионов и обнаружил существование изотопов у большого числа различных химических элементов.
Современные приборы, в которых ионы регистрируются не на фотопластинке, а с помощью электронного устройства, называются масс-спектрометры. Они находят широкое и разнообразное применение в различных областях химии, физики и техники: прецизионное измерение масс ионов, и идентификация и установление структуры многоатомных органических соединений, анализ химического состава смесей и т.д.
§ 1.11. Эффект Холла
Действием силы Лоренца на свободные заряды объясняется явление, открытое в 1880 г. американским физиком Э.Холлом. Он установил, что при прохождении постоянного электрического тока плотностью  через тонкую металлическую пластинку (рис.22), находящуюся в однородном магнитном поле
через тонкую металлическую пластинку (рис.22), находящуюся в однородном магнитном поле  (силовые линии перпендикулярны боковой поверхности пластинки), между параллельными току и полю гранями возникает разность потенциалов
(силовые линии перпендикулярны боковой поверхности пластинки), между параллельными току и полю гранями возникает разность потенциалов 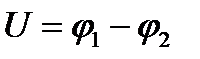 .
.
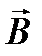
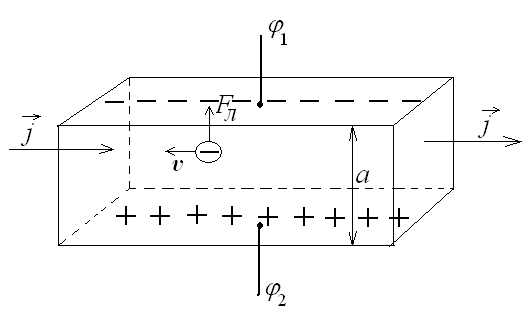
Рис 22.
Экспериментально было установлено, что величина U пропорциональна плотности тока j, индукции магнитного поля В и ширине а пластинки, т.е.
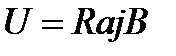 , (1.39),
, (1.39),
где R – постоянная Холла, разная для различных металлов.
Это явление получило название эффекта Холла. Опыты показывают, что эффект Холла наблюдается не только в металлах, но и в полупроводниках. Данный эффект объясняется следующим образом. На электроны, участвующие в упорядоченном движении со скоростью  , рис.22 противоположной по направлению вектору плотности тока
, рис.22 противоположной по направлению вектору плотности тока 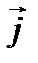 , действует сила Лоренца:
, действует сила Лоренца:
 . (1.40)
. (1.40)
В результате электроны отклоняются к верхней грани пластины, у которой появляется избыточный отрицательный заряд, а у нижней – избыточный положительный заряд. Это приводит к возникновению поперечного электрического поля  , направленного сверху вниз. Разделение зарядов будет происходить до тех пор пока сила
, направленного сверху вниз. Разделение зарядов будет происходить до тех пор пока сила  действует на электроны со стороны поля
действует на электроны со стороны поля  , не уравновесит силу Лоренца:
, не уравновесит силу Лоренца:
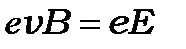 .
.  (1.41)
(1.41)
Из уравнения (1.41) следует, что при  установится стационарное распределение зарядов в поперечном направлении. Тогда разность потенциалов между точками 1 и 2 равна
установится стационарное распределение зарядов в поперечном направлении. Тогда разность потенциалов между точками 1 и 2 равна
 . (1.42)
. (1.42)
Скорость  упорядоченного движения найдём из уравнения
упорядоченного движения найдём из уравнения  :
:  . (1.43)
. (1.43)
Окончательно имеем:
 . (1.44)
. (1.44)
Из сравнения уравнений (1.43), (1.44) следует, что постоянная Холла определяется, как
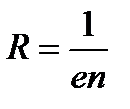 , (1.45)
, (1.45)
где n -концентрация свободных зарядов. Таким образом, измерив на опыте постоянную Холла можно найти концентрацию носителей тока, а по её знаку определить тип проводимости полупроводников: при электронной проводимости R< 0, и при дырочной - R> 0.
Вопросы для самостоятельной работы
1. Опишите опыты Эрстеда и Ампера. В чём их различия и сходства? Что является источником стационарного магнитного поля?
2. Какая величина является силовой характеристикой магнитного поля? Дайте ей определение.
3. Опишите способы определения направления вектора магнитной индукции.
4. Дайте определения линиям магнитной индукции. Сравните свойства линий магнитной индукции с линиями напряженности.
5. Нарисуйте линии магнитной индукции для магнитных полей кругового, прямого и соленоидального тока.
6. Запишите закон Био-Савара-Лапласа в скалярной и векторной форме для элемента тока.
7. В чём заключается принцип суперпозиции для магнитного поля?
8. Какие Вы знаете способы расчёта магнитной индукции. Приведите примеры расчёта магнитных полей прямого и кругового токов.
9. Какой закон подтверждает вихревой характер магнитного поля.
10. Используя закон полного тока, найдите индукцию магнитного поля бесконечного соленоида.
11. В каких случаях проявляется сила Ампера и отчего она зависит.
12. Запишите в векторной форме формулу для силы Ампера. Как определяется её направление?
13. Как действуют на плоский замкнутый контур тока однородное и неоднородное магнитные поля?
14. Что такое магнитный поток или поток вектора магнитной индукции. Чему он равен через любую замкнутую поверхность?
15. Как рассчитывается работа, совершаемая силами магнитного поля при перемещении проводника с током.
16. Какая сила действует на заряженную частицу, движущуюся в магнитном поле? Чему она равна и как направлена?
17. В каких устройствах применяется сила Лоренца, какова роль в них электрического и магнитного полей.
18. В чём состоит эффект Холла и как он объясняется? Глава 2. Электромагнитная индукция
§2.1. Опыты Фарадея. Закон Фарадея и правило Ленца
Из опытов Эрстеда и Ампера следовало, что с помощью электрического тока можно сузить магнитное поле. Следуя идеям о неразрывной связи и взаимодействии сил природы, Фарадей в 1831 г. открыл новое физическое явление электромагнитной индукции, состоящее в возникновении электрического тока с помощью магнитного поля.
Все опыты Фарадея по электромагнитной индукции можно условно разделить на три группы: первая – источник магнитного поля покоится, контур движется (рис.23, а); вторая – источник магнитного поля движется, контур покоится; третья – два неподвижных контура, но в одном из них меняют силу тока (рис.23б). Из этих опытов следовало, что в контуре, соединённом с гальванометром, возникает индукционный ток Ii при всяком изменении магнитного потока, пронизывающего данный контур. По закону Ома электрический ток появляется в замкнутом контуре, если в этой цепи действует ЭДС:
 , (2.1)
, (2.1)
где  - ЭДС электромагнитной индукции возникающая в данном контуре;
- ЭДС электромагнитной индукции возникающая в данном контуре;
R – сопротивление контура. Из рисунка 24а видно, что при перемещении

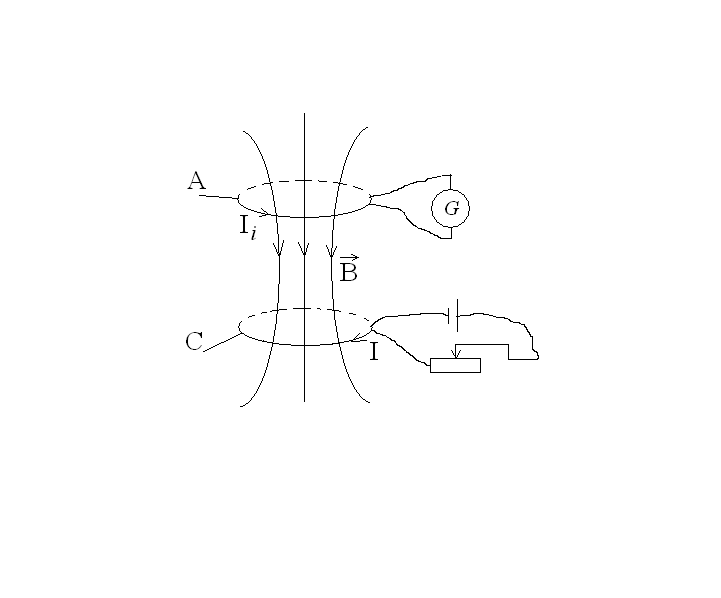
а б
Рис.23.
контура из положения 1 в положение 2, число силовых линий пронизывающих контур растёт, т.е. возрастает магнитный поток. То же самое наблюдается в третьей группе опытов (рис.23б), при росте силы тока в контуре С (рис.23б).
Опыты также показали, что с увеличением скорости движения  контура в магнитном поле или скорости движения магнита относительно контура и быстроты изменения силы тока в контуре С, возникает величина эдс индукции в контуре А (рис.23). Таким образом, Фарадей экспериментально установил, что эдс индукции по абсолютной величине равна скорости изменения магнитного потока, пронизывающего данный контур:
контура в магнитном поле или скорости движения магнита относительно контура и быстроты изменения силы тока в контуре С, возникает величина эдс индукции в контуре А (рис.23). Таким образом, Фарадей экспериментально установил, что эдс индукции по абсолютной величине равна скорости изменения магнитного потока, пронизывающего данный контур:
 , (2.2)
, (2.2)
где Ф – магнитный поток пронизывающий контур площадью S:
 . (2.3)
. (2.3)
Если контур А перемещать из положения 2 в положение 1 (рис.23а), а в контуре С уменьшать силу тока (рис.23б), то направление индукционного тока сменится на противоположное.
Учитывая этот факт, закон Фарадея, выражаемый формулой (2.2), можно переписать, как
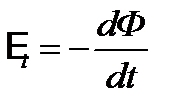 . (2.4)
. (2.4)
Направление индукционного тока определяется правилом Ленца: индукционный ток всегда направлен так, что своим магнитным полем препятствует тому изменению магнитного потока, который вызвал его. Правило Ленца является следствием закона сохранения энергии так, как в противном случае контур А (рис.24а) без видимой причины начал бы ускоряться и увеличивать свою кинетическую энергию.
§ 2.2. Физический смысл эдс индукции
По определению ЭДС индукции можно записать:
 . (2.5)
. (2.5)
Выясним физическую природу сторонних сил  эдс индукции, возникающих в опытах Фарадея.
эдс индукции, возникающих в опытах Фарадея.
Рассмотрим поступательное движение контура со скоростью 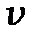 в неоднородном стационарном магнитном поле. Пусть за время dt контур переместился параллельно самому себе из положения L1 в положение L2 на расстояние
в неоднородном стационарном магнитном поле. Пусть за время dt контур переместился параллельно самому себе из положения L1 в положение L2 на расстояние 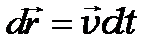 . В положение L1 магнитный поток пронизывающий петлю был равен ФL1. В положении L2 поверхность стягивающая контур увеличилась на величину поверхности ободка Sоб. Таким образом, магнитный поток в положении контура L2 равен
. В положение L1 магнитный поток пронизывающий петлю был равен ФL1. В положении L2 поверхность стягивающая контур увеличилась на величину поверхности ободка Sоб. Таким образом, магнитный поток в положении контура L2 равен
 , (2.6)
, (2.6)
где
 . (2.7)
. (2.7)
Согласно закону Фарадея (2.4), получим
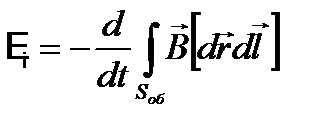 . (2.8)
. (2.8)
Полученный результат справедлив для контура любой формы и движущегося любым способом. Сравнивая уравнения (2.4), (2.5) и (2.8), можно записать
 .
.
Из этого выражения видно, что. в качестве сторонней силы эдс выступает сила Лоренца, которая действует на заряд q, движущийся вместе с контуром.
К такому же выводу можно прийти, рассмотрев следующий пример. Пусть в однородном стационарном магнитном поле  находится контур с подвижной стороной длиной l. Эта сторона может свободно скользить по двум параллельным сторонам контура (рис.24).
находится контур с подвижной стороной длиной l. Эта сторона может свободно скользить по двум параллельным сторонам контура (рис.24).
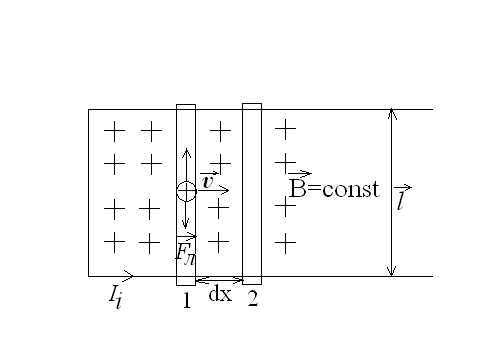
Рис.24.
При перемещении проводника длиной l со скоростью  на dx из положения 1 в положение 2 в контуре возникает индукционный ток. Возникшая эдс индукции по определению равна
на dx из положения 1 в положение 2 в контуре возникает индукционный ток. Возникшая эдс индукции по определению равна
 (2.9)
(2.9)
С другой стороны, на заряд, движущийся вместе с проводником действует сила Лоренца. Эта сила смещает заряд вдоль проводника и совершает работу: 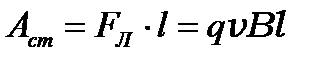 . Тогда эдс индукции
. Тогда эдс индукции
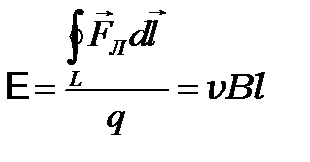 (2.10)
(2.10)
В случае, когда контур покоится, а источник магнитного поля движется, используя принцип относительности, приходим к тому же самому результату: эдс индукции обусловлена возникновением силы Лоренца.
В третьей группе опытов Фарадея оба контура покоятся, но в контуре А возникает эдс индукции и индукционный ток (рис.23б):
 (2.11)
(2.11)
На свободные электрические заряды в контуре может действовать сила Лоренца
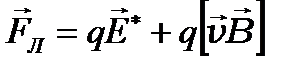
В данном случае магнитная составляющая равна нулю ( ). Остаётся предположить, что возникает электрическое поле
). Остаётся предположить, что возникает электрическое поле  , источником которого является меняющееся во времени магнитное поле:
, источником которого является меняющееся во времени магнитное поле:
 . (2.12)
. (2.12)
Из этого уравнения следует, что циркуляция вектора  не равна нулю:
не равна нулю:  и поле
и поле 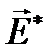 не является потенциальным, оно является вихревым.
не является потенциальным, оно является вихревым.
Таким образом, Фарадей открыл новый вид электрического поля – вихревое электрическое поле, источником которого является меняющееся во времени магнитное поле. Проволочный контур А (рис.23б) играет всего лишь роль индикатора, в котором эдс индукции обусловлена возникновением вихревого электрического поля. Используя уравнение (2.3) перепишем уравнение (2.12):
 (2.13)
(2.13)
Переход к частной производной в первой части связан с тем, что речь идёт об изменении вектора  в определённой точке пространства. Перестановка порядка действий в первой части уравнения допустима, так как дифференцирование выполняется по времени, а интегрирование по поверхности S, стягиваемой контуром L.
в определённой точке пространства. Перестановка порядка действий в первой части уравнения допустима, так как дифференцирование выполняется по времени, а интегрирование по поверхности S, стягиваемой контуром L.
На рис. 25 изображены силовые линии вихревого электрического поля в случаях возрастания (рис.25а) или убывания (рис.25б) магнитного поля со временем.

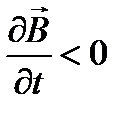
|
|
