Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Электронно-колебательно вращательные спектры

Эти спектры возникают при переходе из одного электронно-колебательно- вращательного состояния в другое. Если

+ +

+ +

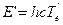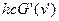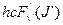
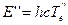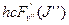
то волновые числа переходов:

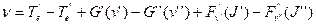
Если не учитывать вращение, то для фиксированных электронных состояний

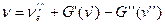
и совокупность наблюдаемых переходов определяется формулой:

= = + -

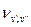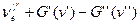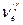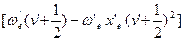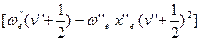
Пусть из экспериментальных данных определены значения 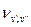для ряда полос и проведено отнесение этих полос к определенным переходам. Тогда получим систему уравнений для определения постоянной 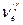- разности электронных термов 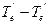, а также колебательных постоянных .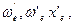

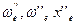Таблица Деландра. Обычно экспериментальные величины 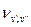располагают в идее таблицы с двумя входами:

v''   v'

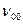
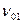
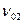
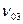
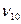
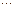
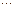
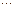
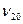
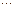
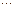
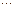
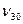
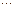
Горизонтальные и вертикальные строчки соответствуют поперечным и продольным сериям (слайд).

Система уравнений для поперечной серии:

=

=

…………………………….

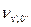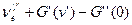
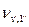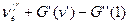
Вычитая каждое последующее уравнение системы из каждого предшествующего получаем:

- = = =

- = = =

………………………………………………………

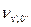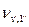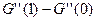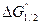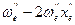
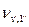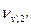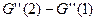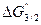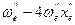
Таким образом получаем колебательные постоянные. Аналогично для верхнего состояния из продольных серий.

Энергия диссоциации. Зная экспериментальные значения колебательных интервалов, можно определить энергию диссоциации:

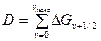
(слайд).