
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
Побудова моделі продуктивності праці.
|
|
Лабораторна робота №1
Тема. Методи побудови загальної економетричної моделі.
Мета. Набути практичних навичок з використанням ПЕОМ у розрахунках показників якості загальної економетричної моделі, перевірці значущості та розрахунках довірчих інтервалів, Етапів дослідження загальної лінійної моделі множинної регресії.
Завдання:
На основі вихідних даних таблиці виконати наведені далі завдання:
1. Побудувати модель продуктивності праці, яка характеризує залежність між рівнем продуктивності праці і чинниками, що впливають на нього (використати 20 спостережень).
2. Оцінити вірогідність моделі та оцінок її параметрів.
3. Визначити прогнозні властивості моделі продуктивності праці.
4. Знайти точковий та інтервальний прогнози продуктивності праці при заданих значеннях чинників на плановий період (останній квартал року).
5. Дати економіко-математичний аналіз моделі. Показати, як можна використати характеристики взаємозв’язку в управлінні рівнем продуктивності праці.
Таблиця 10
| Місяць | Продуктивність праці, гр. од. | Фондомісткість, гр. од. | Коефіцієнт плинності, % | Рівень втрат робочого часу, % | Середній стаж, років |
| 12, 0 | 15, 0 | 8, 0 | |||
| 11, 5 | 14, 3 | 8, 5 | |||
| 11, 0 | 12, 0 | 7, 0 | |||
| 10, 0 | 12, 8 | 9, 0 | |||
| 9, 0 | 13, 0 | 10, 0 | |||
| 8, 0 | 12, 5 | 11, 0 | |||
| 7, 5 | 11, 0 | 9, 5 | |||
| 7, 2 | 11, 5 | 12, 0 | |||
| 7, 0 | 10, 0 | 10, 0 | |||
| 4, 5 | 9, 0 | 14, 0 | |||
| 4, 0 | 8, 0 | 12, 5 | |||
| 3, 7 | 7, 5 | 12, 0 | |||
| 3, 6 | 6, 5 | 10, 0 | |||
| 3, 0 | 6, 0 | 11, 0 | |||
| 3, 1 | 6, 2 | 12, 0 | |||
| 3, 2 | 5, 8 | 15, 0 | |||
| 3, 5 | 5, 5 | 15, 5 | |||
| 3, 0 | 5.0 | 14, 5 | |||
| 3, 0 | 4, 5 | 14, 0 | |||
| 2, 0 | 4, 7 | 15, 0 | |||
| 3, 0 | 5, 0 | 15, 0 | |||
| 4, 0 | 5, 1 | 16, 5 | |||
| 4, 0 | 4, 8 | 15, 7 | |||
| 5, 0 | 5, 2 | 15, 8 |
Розв’язування:
Побудова моделі продуктивності праці.
Щоб виконати поставлене завдання, скористаємося пакетом Excel.
Ідентифікуємо змінні моделі:
Y - продуктивність праці, залежна змінна, результативна ознака;
X1- фондомісткість, незалежна змінна, пояснювальна;
X2- коефіцієнт плинності, незалежна змінна, пояснювальна;
X3- рівень втрат робочого часу, незалежна змінна, пояснювальна;
X4- середній стаж, незалежна змінна, пояснювальна.
Специфікуємо модель:
Загальний вигляд моделі продуктивності праці такий:
Y = f(X1 , X2 , X3, X4, u).
Аналітичний вигляд моделі подамо у двох формах.
Специфікуємо модель у лінійній формі:
Y = a0 + a1 X1 + a2 X2 + a3 X3 + a4 X4 + u – теоретична модель;
Ŷ = â 0 + â 1 X1 + â 2 X2 + â 3 X3 + â 4 X4 – розрахункова модель;
u = Y – Ŷ – залишки, стохастична складова.
На підставі 20 спостережень (n = 20), використовуючи 1МНК, побудуємо економетричну модель для лінійної і степеневої функцій.
Побудувати економетричну модель – це означає кількісно оцінити вектор Â, тобто його компоненти. Це будуть параметри цієї моделі. Вектор Â має вигляд:
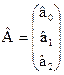
Оцінимо параметри методом 1 МНК. Оператором оцінювання методу 1 МНК є матричний оператор:
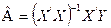 ,
,
де X – матриця пояснюючих змінних,
Y – вектор залежної змінної;
XТ – матриця транспортована до матриці X (ТРАНСП)[1].
Крок 1. Формуємо матриці Х, У, XТ
Крок 2. Помножимо матрицю XТ на матрицю X (МУМНОЖ)[2].
Крок 3. Помножимо матрицю XТ на матрицю Y та обернемо добуток (XТX) (МОБР)[3].
Крок 4. Перемноживши дві останні матриці, отримаємо оператор оцінювання (МУМНОЖ)[4]:
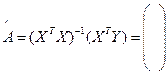


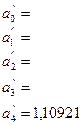
Отже, економетрична лінійна модель, яка виражає залежність між витратами на харчування, загальними витратами та складом сім’ї, має вигляд:
Ŷ = â 0 + â 1 X1 + â 2 X2 + â 3 X3 + â 4 X4
Крок 5. 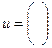
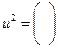
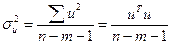 =
=
Дисперсійно-коваріаційна матрица:
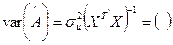
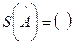
Результати розрахунку економетричної моделі на основі стандартної програми ЛИНЕЙН:
Лінійна модель:
| 1, 10920465 | ||||
| 0, 65800188 | ||||
| #Н/Д | #Н/Д | #Н/Д | ||
| #Н/Д | #Н/Д | #Н/Д | ||
| #Н/Д | #Н/Д | #Н/Д |
Пояснимо, що в якому рядку знаходитимуся:
Для лінійної моделі:
| â 4 | â 3 | â 2 | â 1 | â 0 |
| 1, 10920465 | ||||
| Sâ 4 | Sâ 3 | Sâ 2 | Sâ 1 | Sâ 0 |
| 0, 65800188 | ||||
| R2 | 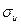
| |||
| #Н/Д | #Н/Д | #Н/Д | ||
| F | (n-m) | |||
| #Н/Д | #Н/Д | #Н/Д | ||
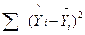
| 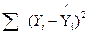
| |||
| #Н/Д | #Н/Д | #Н/Д |
Перший рядок містить оцінки параметрів моделі.
Другий рядок містить стандартні похибки оцінок параметрів моделі.
Третій рядок містить два показники R2 і 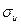 .
.
Четвертий рядок містить два показники F-критерій та ступені свободи (n-m).
П’ятий (останній) рядок містить два показники - суму квадратів регресії та суму квадратів залишків.
|
|
