
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
Интегрирование рациональных дробей. Метод Остроградского
|
|
Сформулируем общее правило интегрирования рациональных дробей.
1. Если дробь неправильна, то представить ее в виде суммы многочлена и правильной дроби.
2. Разложив знаменатель правильной рациональной дроби на множители, представить ее в виде суммы простейших рациональных дробей.
3. Проинтегрировать многочлен и полученную сумму простейших дробей.
Метод Остроградского
Если знаменатель правильной рациональной дроби имеет кратные корни, то интегрирование связано с громоздкими выкладками. В этом случае удобно пользоваться формулой Остроградского:
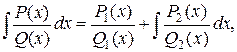
где 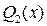 – многочлен, имеющий те же корни, что и
– многочлен, имеющий те же корни, что и 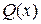 , но кратности 1;
, но кратности 1; 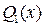 – частное от деления
– частное от деления 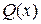 на
на 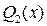 ;
; 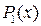 и
и 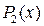 – многочлены, степени которых соответственно меньше степеней многочленов
– многочлены, степени которых соответственно меньше степеней многочленов 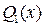 и
и 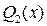 . Для отыскания многочленов
. Для отыскания многочленов 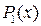 и
и 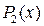 их записывают с неопределённым коэффициентом, которые находятся после дифференцирования обеих частей формулы Остроградского.
их записывают с неопределённым коэффициентом, которые находятся после дифференцирования обеих частей формулы Остроградского.
Пример. Найдём методом Остроградского интеграл 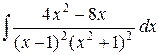
В этом случае  , поэтому
, поэтому
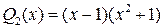 ,
, 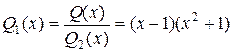
Следовательно, существуют многочлены 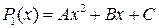 и
и 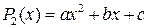 , для которых верно:
, для которых верно:
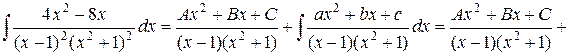
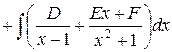 .
.
Дифференцируя обе части этого равенства получаем:
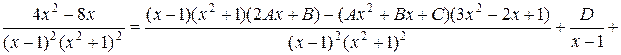
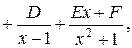
Откуда вытекает равенство многочленов 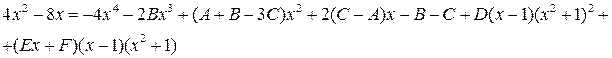
Приравнивая коэффициенты при одинаковых степенях 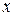 , получаем:
, получаем: 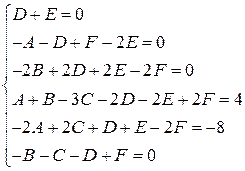
Решая эту систему, находим 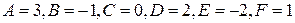 . Итак,
. Итак,
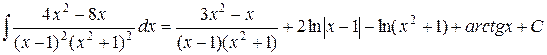
Метод Остроградского является общим: с его помощью можно вычислить интеграл от любой рациональной дроби, при условии, что могут быть найдены все корни знаменателя. Следует иметь в виду, что другие приёмы во многих частных случаях быстрее ведут к цели.
3.1 Найти интегралы (знаменатель имеет действительные корни, но среди них нет кратных):
1 а)  ; б)
; б) 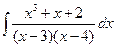 ; в)
; в) 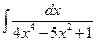 ;
;
2 а) 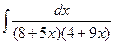 ; б)
; б) 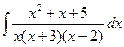 ; в)
; в) 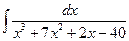 ;
;
3 а) 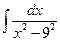 ; б)
; б) 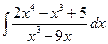 ; в)
; в) 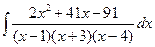 ;
;
4 а) 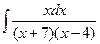 ; б)
; б) 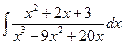 ; в)
; в) 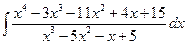 ;
;
5 а) 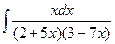 ; б)
; б) 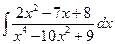 ; в)
; в) 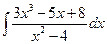 ;
;
6 а) 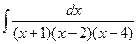 ; б)
; б) 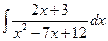 ; в)
; в)  ;
;
7 а) 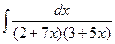 ; б)
; б) 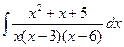 ; в)
; в) 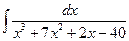 ;
;
8 а) 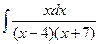 ; б)
; б) 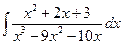 ; в)
; в) 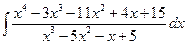 ;
;
9 а) 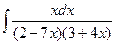 ; б)
; б) 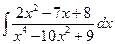 ; в)
; в) 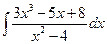 ;
;
10 а) 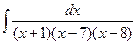 ; б)
; б) 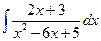 ; в)
; в)  .
.
3.2 Найти интегралы (знаменатель имеет действительные корни и среди них есть кратные):
1 a) 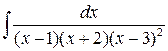 ; б)
; б) 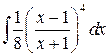 ;
;
2 a) 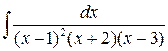 ; б)
; б) 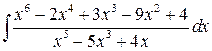 ;
;
3 а) 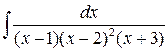 ; б)
; б) 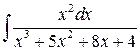 ;
;
4 а) 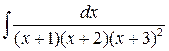 ; б)
; б) 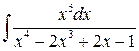 ;
;
5 а) 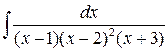 ; б)
; б) 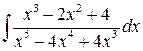 ;
;
6 а) 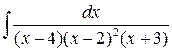 ; б)
; б) 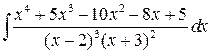 ;
;
7 а) 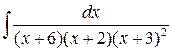 ; б)
; б) 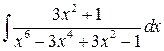
8 а) 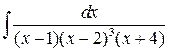 ; б)
; б) 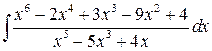 ;
;
9 а) 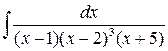 ; б)
; б) 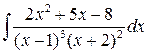 ;
;
10 а)  ; б)
; б) 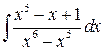 .
.
3.3 Найти интегралы (знаменатель содержит множители, которые не имеют действительных корней):
* Замечание. Для решения некоторых примеров потребуется применение формул сокращенного умножения, например, формулы «сумма кубов».
1 а) 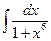 ; б)
; б) 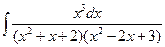 ; в)
; в) 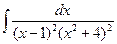 ;
;
2 а) 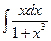 ; б)
; б) 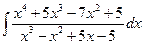 ; в)
; в) 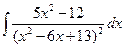 ;
;
3 а) 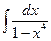 ; б)
; б) 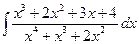 ; в)
; в) 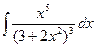 ;
;
4 а) 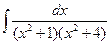 ; б)
; б) 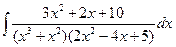 ; в)
; в) 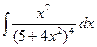 ;
;
5 а) 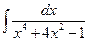 ; б)
; б)  ; в)
; в)  ;
;
6 а) 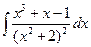 ; б)
; б) 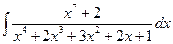 ; в)
; в) 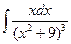 ;
;
7 а) 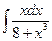 ; б)
; б) 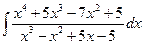 ; в)
; в) 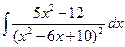 ;
;
8 а) 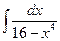 ; б)
; б) 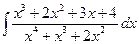 ; в)
; в) 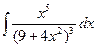 ;
;
9 а) 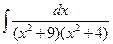 ; б)
; б) 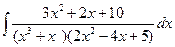 ; в)
; в) 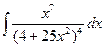 ;
;
10 а) 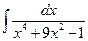 ; б)
; б) 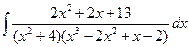 ; в)
; в) 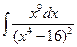 .
.
Замечание. Интегралы вида  легко вычисляются с помощью подстановки a+bx2=t.
легко вычисляются с помощью подстановки a+bx2=t.
3.4 Применяя метод Остроградского, найти интеграл из №3.3(в).
|
|
