Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Коды, обнаруживающие и исправляющие ошибки передачи. Построение систематического кода. Код Хемминга.

В настоящее время основным способом обеспечения достоверности сообщения при их передаче по каналам связи при воздействии помех (шумов) является помехоустойчивое кодирование. Эффективность такого кодирования достигается за счёт введения искусственной избыточности в передаваемое сообщение, что приводит к расширению используемой полосы частот и уменьшению информационной скорости передачи.

Многообразие существующих помехоустойчивых кодов делится на два класса: блочные и непрерывные коды. В блочных кодах передаваемая информационная последовательность разбивается на отдельные блоки с добавлением каждому блоку определённого числа проверочных символов. Кодовые комбинации кодируются и декодируются независимо друг от друга. В непрерывных кодах, передаваемая информационная последовательность не разделяется на блоки, а проверочные символы размещаются в определённом порядке между информационными. Процессы кодирования и декодирования также осуществляются в непрерывном режиме.

Систематический код – это код, в котором разряды распределены на две группы, одна из которых служит, для передачи информации, а вторая – для проверки правильности передачи, причём все разряды занимают строго фиксированные положения.

Рассмотрим построение систематического кода на примере кода Хэмминга.

Коды Хэмминга – это наиболее известные, и, вероятно первые из самоконтролирующихся и самокорректирующихся кодов. Другими словами, это алгоритм, который позволяет закодировать какое-либо информационное сообщение определённым образом и после передачи определить появилась ли какая-то ошибка в этом сообщении (к примеру из-за помех) и, при возможности восстановить это сообщение.

Для того, чтобы понять работу данного алгоритма, рассмотрим пример:

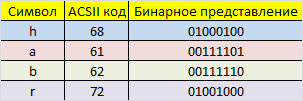Допустим есть сообщение «habr», которое необходимо передать без ошибок. Для этого нужно наше сообщение закодировать при помощи кода Хэмминга. Нам необходимо представить его в бинарном виде.

На этом этапе стоит определиться с так называемой, длиной информационного слова, то есть длиной строки из нулей и единиц, которые мы будем кодировать. Допустим, у нас длина слова будет равна 16 бит. Таким образом, нам необходимо разделить наше исходное сообщение («habr») y блоки по 16 бит, которые мы будем потом кодировать отдельно друг от друга. Так как один символ занимает в памяти 8 бит, то в одно кодируемое слово помещается ровно два ASCII символа. Итак, мы получили две бинарные строки по 16 бит:

После этого процесс кодирования распараллеливается, и две части сообщения («ha» и «br») кодируются независимо друг от друга. Рассмотрим как это делается на примере первой части.

Прежде всего необходимо вставить контрольные биты. Они вставляются в строго определённых местах – это позиции с номерами, равными степеням двойки. В нашем случае (при длине информационного слова в 16 бит) это будут позиции 1, 2, 4, 8, 16. Соответственно получилось 5 контрольных бит.

Было:

Стало:

При этом длина сообщения увеличилась на 5 бит.

Теперь необходимо вычислить значение каждого контрольного бита. Значение каждого контрольного бита зависит от значений информационных бит, но не от всех, а только от тех, который этот контрольный бит контролирует. Для того, чтобы понять, за какие биты отвечает каждых контрольный бит необходимо понять очень простую закономерность: контрольный бит с номером N контролирует все последующие N бит через каждые N бит, начиная с позиции N. Не очень понятно, но по картинке, думаю, станет яснее:

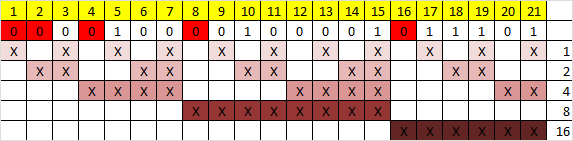
Здесь знаком «X» обозначены те биты, которые контролирует контрольный бит, номер которого справа. То есть, к примеру, бит номер 12 контролируется битами с номерами 4 и 8. Ясно, что чтобы узнать какими битами контролируется бит с номером N надо просто разложить N по степеням двойки.

Но как же вычислить значение каждого контрольного бита? Делается это очень просто: берём каждый контрольный бит и смотрим сколько среди контролируемых им битов единиц, получаем некоторое целое число и, если оно чётное, то ставим ноль, в противном случае ставим единицу.

Высчитав контрольные биты для нашего информационного слова получаем следующее:

и для второй части:

Вот и всё! Первая часть алгоритма завершена.

Теперь, допустим, мы получили закодированное первой частью алгоритма сообщение, но оно пришло к нас с ошибкой. К примеру мы получили такое (11-ый бит передался неправильно):

Вся вторая часть алгоритма заключается в том, что необходимо заново вычислить все контрольные биты (так же как и в первой части) и сравнить их с контрольными битами, которые мы получили. Так, посчитав контрольные биты с неправильным 11-ым битом мы получим такую картину:

Как мы видим, контрольные биты под номерами: 1, 2, 8 не совпадают с такими же контрольными битами, которые мы получили. Теперь просто сложив номера позиций неправильных контрольных бит (1 + 2 + 8 = 11) мы получаем позицию ошибочного бита. Теперь просто инвертировав его и отбросив контрольные биты, мы получим исходное сообщение в первозданном виде! Абсолютно аналогично поступаем со второй частью сообщения.