
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Информация и энтропия. Измерение количества информации. Свойства информации. Формулы Хартли и Шеннона.
|
|
Основоположник теории информации Клод Шеннон определил информацию как снятую неопределённость. Точнее сказать, получение информации – необходимое условие для снятия неопределённости. Неопределённость возникает в ситуации выбора. Задача, которая решается в ходе снятия неопределённости – уменьшение количества рассматриваемых вариантов (уменьшение разнообразия), и в итоге выбор одного варианта, соответствующего ситуации из числа возможных. Снятие неопределённости дает возможность принимать обоснованные решения и действовать.
Представьте, что вы зашли в магазин и попросили продать вам жевательную резинку. Продавщица, у которой, скажем, 16 сортов жевательной резинки, находится в состоянии неопределенности. Она не может выполнить вашу просьбу без получения дополнительной информации. Если вы уточнили, скажем, - «Orbit», и из 16 первоначальных вариантов продавщица рассматривает теперь только 8, вы уменьшили ее неопределенность в два раза (забегая вперед, скажем, что уменьшение неопределенности вдвое соответствует получению 1 бита информации). Если вы, не мудрствуя лукаво, просто указали пальцем на витрине, - «вот эту!», то неопределенность была снята полностью. Опять же, забегая вперед, скажем, что этим жестом в данном примере вы сообщили продавщице 4 бита информации.
Ситуация максимальной неопределённости предполагает наличие нескольких равновероятностных альтернатив (вариантов), т.е. ни один из вариантов не является более предпочтительным. Причём, чем больше равновероятностных вариантов наблюдается, тем больше неопределённость, тем сложнее сделать однозначный выбор и тем больше информации требуется для этого получить. Для N вариантов эта ситуация описывается следующим распределением вероятностей: {1/N, 1/N, … 1/N).
Минимальная неопределённость равна 0, т.е. эта ситуация полной определённости, означающая, что выбор сделан, и вся необходимая информация получена. Распределение вероятностей для ситуации полной определённости выглядит так: {1, 0, … 0}.
Величина, характеризующая количество неопределённости в теории информации обозначается символом H и имеет название энтропия, точнее информационная энтропия.
Энтропия выражается в битах.
Количество информации (I) и энтропия (H) характеризуют одну и ту же ситуацию, но с качественно противоположных сторон. I – это количество информации, которое требуется для снятия неопределённости (Н).
Формула Шеннона имеет следующий вид:
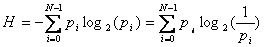
Знак минус в формуле не означает, что энтропия – отрицательная величина. Объясняется это тем, что pi£ 1 по определению, а логарифм числа меньше единицы – величина отрицательная. По свойству логарифма 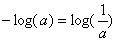 .
.
Приведем пример расчета энтропии по формуле Шеннона. Пусть в некотором учреждении состав работников распределяется так: ¾ - женщины, ¼ - мужчины. Тогда неопределенность, например, относительно того, кого вы встретите первым, зайдя в учреждение, будет рассчитана рядом действий, показанных в таблице 1.
Таблица 1.
| pi | 1/pi | Ii=log2(1/pi), бит | pi*log2(1/pi), бит | |
| Ж | 3/4 | 4/3 | log2(4/3)=0, 42 | 3/4 * 0, 42=0, 31 |
| М | 1/4 | 4/1 | log2(4)=2 | 1/4 * 2=0, 5 |
| å | 1 | H=0, 81 бит |
Формула Хартли – частный случай формулы Шеннона для равновероятностных альтернатив.
Формула Хартли выглядит очень просто:
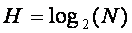
Из неё явно следует, чем больше количество альтернатив (N), тем больше неопределённость (Н)
Например:
В доме 8 этажей, какое количество информации мы получили, узнав, что интересующий нас Коля Иванов живет на втором этаже? ”, нужно воспользоваться формулой (2): I=log28=3 бита.
 36. Общая схема передачи информации. Канал связи. Характеристики канала: ширина полосы пропускания, пропускная способность, скорость передачи. Влияние шумов на пропускную способность канала. Вторая теорема Шеннона. Обеспечение надежности передачи.
36. Общая схема передачи информации. Канал связи. Характеристики канала: ширина полосы пропускания, пропускная способность, скорость передачи. Влияние шумов на пропускную способность канала. Вторая теорема Шеннона. Обеспечение надежности передачи.
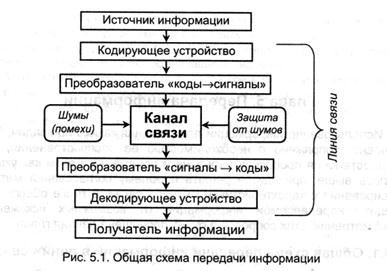
Использование информации связано с необходимостью её распространения, т.е. осуществления процессов передачи и приёма. Рассмотрим схему передачи информации:
Источник, порождающий информацию, для передачи должен представить её в виде сообщения, т.е. последовательности сигналов, используя некоторую систему кодирования. Далее коды переводятся в последовательность материальных сигналов преобразователем. После преобразования сигналы поступают и распространяются по линии связи.
Любая реальная линия связи подвержена внешним воздействиям, а также в ней могут происходить внутренние процессы, в результате которых искажаются передаваемые сигналы и, следовательно, связанное с ними сообщение. Такие воздействия называются шумами (помехами). Источники помех могут быть внешними или внутренними.
После прохождения сообщения по линии связи сигналы с помощью приёмного преобразователя переводятся в последовательность кодов, которые декодирующим устройством представляются в форме, необходимой приёмнику информации. Канал связи объединяет все элементы, находящиеся между источником и приёмником информации.
Каналы передачи информации могут использовать различные физические принципы. Так, при непосредственном общении людей информация передаётся с помощью звуковых волн, а при разговоре по телефону – с помощью электрических сигналов, которые распространяются по линиям связи.
Канал связи – это технические средства, позволяющие осуществить передачу данных на расстоянии.
Компьютеры могут обмениваться информацией с использованием каналов связи различной физической природы: кабельных, оптоволоконных, радиоканалов и т.д.
Скорость передачи информации – это количество информации, передаваемое за единицу времени.
Общая схема передачи информации включает в себя отправителя информации, канал передачи информации и получателя информации.
Основной характеристикой канала передачи информации является пропускная способность.
Пропускная способность – максимальная скорость передачи информации по каналу связи.
Как уже говорилось на сигналы передаваемые по каналу связи действуют помехи (шумы). Вторая теорема Шеннона гласит, что при наличии помех в канале связи всегда можно найти такую систему кодирования, при которой сообщения будут переданы с заданной достоверностью.
Избыточность информации при передаче сообщений имеет свои положительные и отрицательные стороны. Увеличение избыточности приводит к увеличению времени передачи сообщений, излишней нагрузке каналов связи.
Однако при увеличении избыточности появляется возможность повышения помехоустойчивости при передачи сообщений. Так, избыточность текста позволяет исправлять отдельные ошибки или восстанавливать пропущенные буквы или даже слова в телеграмме. Для систем связи устанавливается компромиссное значение избыточности, которое обеспечивает заданную скорость и надёжность передачи сообщений.
|
|