💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Методические указания 2 страница

где 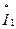- комплексный первый ток;

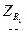- комплексное сопротивление резистора ;

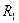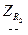- комплексное сопротивление резистора ;

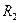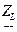- комплексное сопротивление катушки L.

Определяем комплексное входное сопротивление цепи:

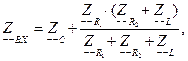(1.6)

где 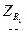- комплексное сопротивление резистора ;

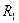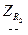- комплексное сопротивление резистора ;

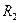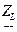- комплексное сопротивление катушки L.

После элементарных преобразований комплексное входное сопротивление

цепи принимает вид:

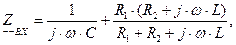(1.7)

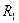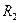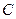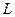где , , , и 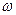- индивидуальные численные значения выбранные для своего варианта и соответственно равные 170 Ом, 270 Ом, 40 мкФ, 2мГн, а j – комплексная постоянная численно равная .

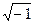Полученное выражение для комплексного входного сопротивления четырехполюсника (1.7) подставляем в выражение для первого тока (1.3), тогда получим:

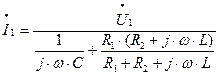(1.8)

Полученное выражение для первого тока (1.8) подставляем в выражение для второго тока (1.4) и получаем следующее выражение:

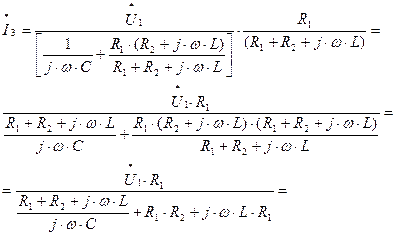
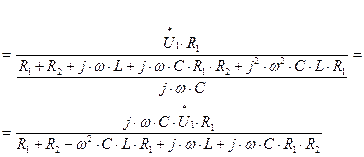(1.9)

Определяем комплексное выходное напряжение заданной цепи, подставляя выражение второго тока (1.9) в выражение (1.2):

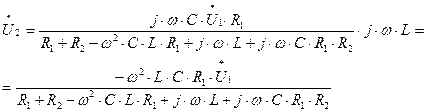(1.10)

Подставляем полученную дробь (1.10) в выражение для получения комплексного коэффициента передачи по напряжению (1.1):

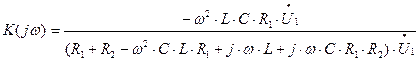(1.11)

После сокращения выражение для комплексного коэффициента передачи принимает вид:

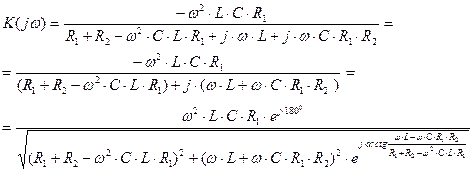
(1.12)

Комплексный коэффициент передачи по напряжению в показательной форме имеет вид:

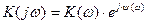(1.13)

где 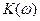- модуль коэффициента передачи по напряжению, соответственно являющийся функцией АЧХ;

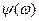- аргумент коэффициента передачи по напряжению, соответственно являющийся функцией ФЧХ.

В результате аналитические выражения для АЧХ и ФЧХ представляют собой соответственно:

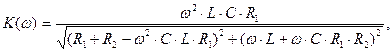(1.14)

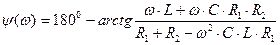(1.15)

Анализ аналитических выражений и графиков частотных характеристик цепей позволяет сделать выводы об их избирательных свойствах, коэффициентах передачи, о возможности резонансных явлений.

Графики АЧХ и ФЧХ построены в системе Mathcad 2001 Professional и приведены в Приложении А.

Таблица 1.1 – Данные для расчета АЧХ и ФЧХ

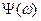
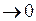
		0o
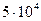
	0.1	-52.11o
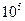
	0.15	-44.44o
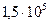
	0.165	-36.51o
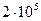
	0.169	-29.34o
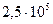
	0.170	-24.2o
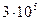
	0.170	-20.4
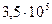
	0.171	-18.05
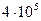
	0.171	-16.07
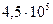
	0.171	-14.033
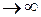
	0.171	0о

2 Расчет переходной характеристики четырехполюсника

Переходной характеристикой линейной цепи, не содержащей независимых источников энергии, называется отношение реакции этой цепи на воздействие неединичного скачка напряжения или тока к высоте этого скачка при нулевых начальных условиях:

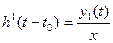(2.1)

Из выражения (2.1) видно, что 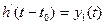, если , следовательно, переходная характеристика цепи численно равная реакции на воздействие единичного скачка тока или напряжения. Размерность переходной характеристики равна отношению размерности отклика цепи к размерности внешнего воздействия.

Единичной ступенчатой функцией (функцией Хевисайда) называется функцией:

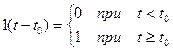(2.2)

Функцией Хевисайда удобно использовать для аналитического представления различных воздействий на цепь, значения которых скачкообразно изменяются в момент коммутации.

Переходная характеристика будет рассчитываться двумя методами: классическим и операторным.

Общая схема применения классического метода анализа переходных процессов

Определим основные этапы классического метода анализа переходных процессов в линейных инвариантных во времени цепях с сосредоточенными параметрами.

Анализ цепи до коммутации. В результате этого анализа определяют токи индуктивностей и напряжений емкостей в момент времени, непосредственно предшествующий коммутации .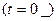

Определение независимых начальных условий. Независимые начальные условия представляют собой токи индуктивностей и напряжения емкостей в момент времени 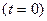. Независимые начальные условия находят с помощью законов коммутации или принципа непрерывности потокосцепления и электрического заряда цепи.

Составление дифференциального уравнения цепи после коммутации (при 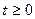). Дифференциальное уравнение цепи получают из системы уравнений электрического равновесия цепи, составленной любым методом, путем исключения всех известных величин, кроме одной, представляющей собой ток или напряжение какой - либо ветви.

Анализ установившегося процесса в цепи после коммутации (при 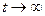). В результате анализа установившегося процесса в цепи после коммутации находят принужденную составляющую реакции цепи (частное решение дифференциального уравнения цепи).

Определение свободной составляющей цепи. На этом этапе составляют характеристическое уравнение цепи, находят его корни и определят общий вид свободной составляющей реакции цепи (общее решение однородного дифференциального уравнения, соответствующего дифференциальному уравнению цепи после коммутации).

Нахождение общего вида реакции цепи. Общий вид реакции цепи (общее решение дифференциального уравнения цепи) находят путем суммирования свободной и принужденных составляющих реакции цепи.

Определение постоянных интегрирования. Постоянные интегрирования

находят по зависимым начальным условиям (значениям искомых токов или напряжений и их производных первой степени в начальный момент времени после коммутации). Для определения зависимых начальных условий используют независимые начальные условия и уравнения электрического равновесия цепи после коммутации.

Определение реакции цепи, соответствующей заданным начальным условиям. Подставляя постоянные интегрирования в общее решение дифференциального уравнения цепи после коммутации, находят частое решение дифференциального уравнения, соответствующее заданным начальным условиям, т.е. искомый ток или напряжение одной из ветвей при .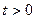

Общая схема применения операторного метода анализа переходных процессов

Определим основные этапы анализа переходных процессов в линейных цепях с помощью операторного метода.

Анализ цепи до коммутации и определение независимых начальных условий. Выполняются так же, как и при использовании классического метода анализа переходных процессов.

Составление операторной эквивалентной схемы цепи после коммутации. Составление операторной эквивалентной схемы производится непосредственно по эквивалентной схеме цепи для мгновенных значений путем замены каждого идеализированного пассивного элемента его операторной схемой замещения и представления токов и напряжений идеализированных источников тока или напряжения их операторными изображениями.

Решение уравнений электрического равновесия цепи относительно изображений искомых токов и напряжений. Может производиться любым методом, в том числе путем использования метода сигнальных графов.

Определение оригиналов искомых токов и напряжений. Как правило, производится путем применения таблиц обратного преобразования Лапласа и использования основных свойств преобразования Лапласа. Если изображение интересующей функции представляет собой отношение двух полиномов 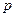, для выполнения обратного преобразования Лапласа можно воспользоваться теоремой разложения.

Общий вид свободной составляющей реакции цепи (общее решение однородного дифференциального уравнения, соответствующего дифференциальному уравнению цепи после коммутации) определяется корнями характеристического уравнения. Корни характеристического уравнения могут быть вещественными различными или комплексно – сопряженными в зависимости от соотношения параметров цепи. Рассмотрим каждый из этих случаев.

2.1 Расчет переходной характеристики цепи классическим методом в случае вещественных различных корней

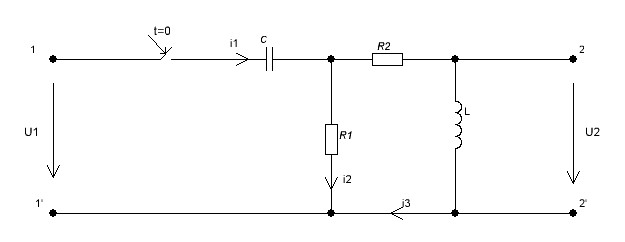
Рисунок 2.1 – Рассчитываемая цепь до коммутации

До коммутации токи во всех ветвях электрической цепи и напряжения на всех элементах равны нулю:

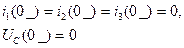(2.3)

Используя законы коммутации, нахожу независимые начальные условия, представляющие собой ток индуктивности и напряжение ёмкости в момент времени (t=0).

(2.4)

Составим систему дифференциальных уравнений на основании законов Кирхгофа, описывающую процесс в цепи после коммутации (t> 0):

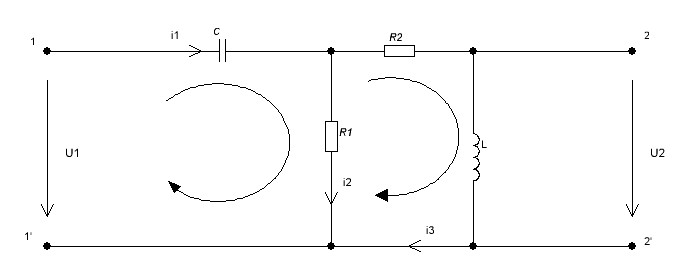
Рисунок 2.2 – Рассчитываемая цепь после коммутации

Выбираю произвольно направление обхода контура (рисунок 2.2), .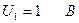

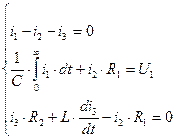(2.5)

Токи в цепи представим в виде суммы установившегося и свободного режима цепи:

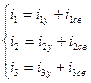(2.6)

где 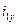- установившаяся составляющая первого тока;

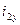- установившаяся составляющая второго тока;

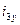- установившаяся составляющая третьего тока;

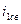- свободная составляющая первого тока;

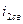- свободная составляющая второго тока;

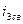- свободная составляющая третьего тока.

Определим установившиеся токи и напряжения, так как на входе цепи четырехполюсника ёмкость (рисунок 2.2), то значения установившихся токов будут равны нулю:

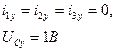(2.7)

Определим токи и напряжения свободного режима. Запишем характеристическое уравнение цепи. Наиболее простой способ составления характеристического уравнения – это метод входного сопротивления. Запишем входное сопротивление цепи в комплексной форме.

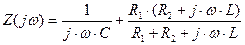(2.8)

Заменяем в выражении (2.8) 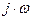на 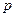и приравниваем его к нулю:

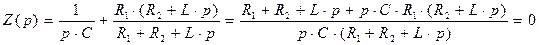
(2.9)

Приравняем к нулю числитель выражения (2.9):

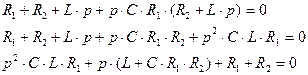(2.10)

Уравнение (2.9) является характеристическим уравнением цепи. Характеристическое уравнение цепи можно составить другим способом. Запишем определитель исходной системы уравнений и приравниваем его к нулю:

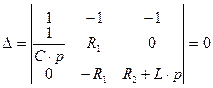(2.11)

Выполнив необходимые преобразования, получим:

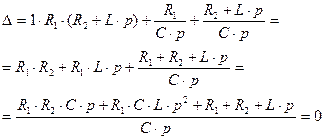(2.12)

Приравняв к нулю числитель выражения (2.12), получим:

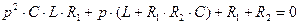(2.13)

Полученное квадратное уравнение (2.13) полностью совпадает с квадратным уравнением (2.10).Обоими способами были получены абсолютно идентичные уравнения и соответственно можно сделать вывод, что расчеты выполнены правильно.

Подставив числовые значения параметров цепи в характеристическое уравнение (2.13), вычислим его корни:

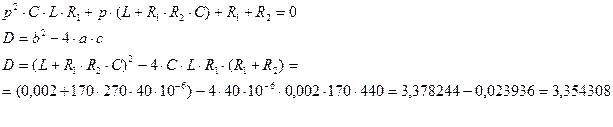
(2.14)

Дискриминант получился 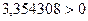, находим корни:

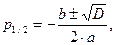(2.15)

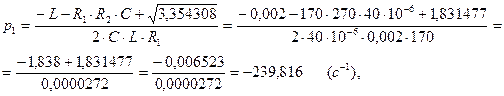(2.16)

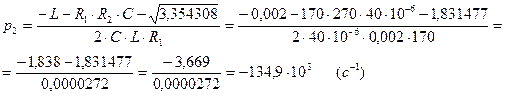(2.17)

Корни характеристического уравнения – вещественные числа, характер переходного процесса апериодический, свободные составляющие тока запишем в виде:

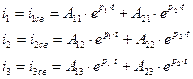(2.18)

где 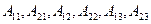- постоянные интегрирования.

Для расчета постоянных интегрирования определим зависимые начальные условия. Запишем исходную систему уравнений (2.5) для :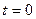

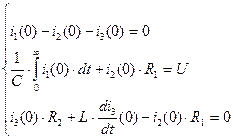(2.19)

Находим численные значения токов :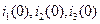

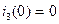- из независимых начальных условий; (2.20)

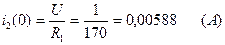(2.21)

Так как 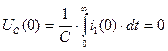из независимых начальных условий;

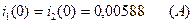(2.22)

Из третьего уравнения системы (2.19) выражаем и находим :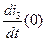

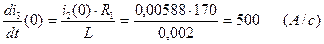(2.23)

Для определения 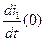и 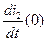продифференцируем первое и второе уравнение из системы уравнений (2.19) и запишем для :

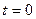(2.24)

Из второго уравнения системы уравнений (2.24) найдем :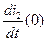

(2.25)

Найдем, 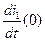подставив известные численные значения 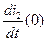(2.25) и 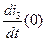(2.23) в первое уравнение системы уравнений (2.24):

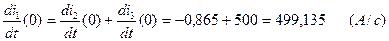(2.26)

Определим постоянные интегрирования. Так как установившиеся составляющие всех токов равны нулю, то токи в цепи будут определяться только их свободными составляющими:

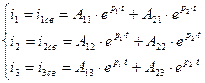(2.27)

Продифференцируем систему уравнений для токов (2.27) и запишем их для :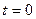

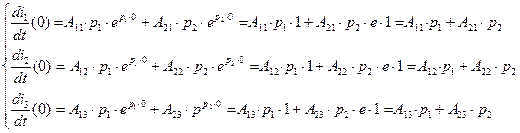(2.28)

Запишем систему уравнений (2.27) для :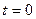

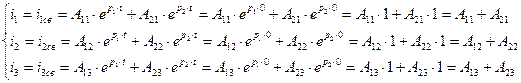(2.29)

Из двух систем уравнений (2.28) и (2.29) запишем три парные системы уравнений:

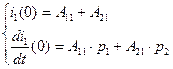(2.30)

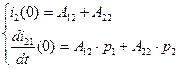(2.31)

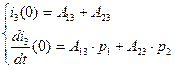(2.32)

Решаем систему уравнений (2.30). Выражаем из первого уравнения 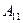и подставляем полученное выражение во второе уравнение той же системы уравнений:

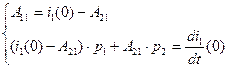(2.33)

Подставляем во второе уравнение системы уравнений (2.33) ранее подсчитанные значения 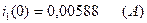(2.22), 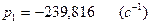(2.16), 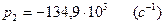(2.17) и 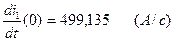(2.26). Преобразуем, выражение и находим значение :

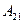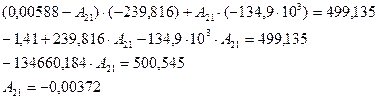(2.34)

Полученное значение 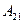подставляем в первое уравнение системы уравнений (2.33) и находим :

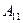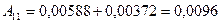(2.35)

Решаем систему уравнений (2.31). Выражаем из первого уравнения 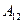и подставляем полученное выражение во второе уравнение той же системы уравнений:

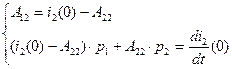(2.36)

Подставляем во второе уравнение системы уравнений (2.36) ранее подсчитанные значения 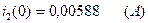(2.21), 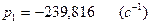(2.16), 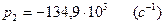(2.17) и (2.25). Преобразуем, выражение и находим значение :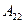

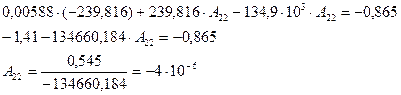(2.37)

Полученное значение 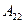подставляем в первое уравнение системы уравнений (2.37) и находим :

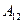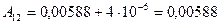(2.38)

Решаем систему уравнений (2.32). Выражаем из первого уравнения 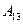и подставляем полученное выражение во второе уравнение той же системы уравнений:

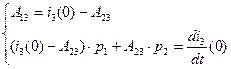(2.39)

Подставляем во второе уравнение системы уравнений (2.39) ранее подсчитанные значения 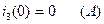(2.20), 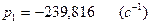(2.16), 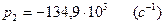(2.17) и 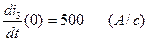(2.23). Преобразуем, выражение и находим значение :

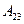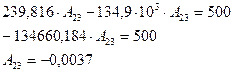(2.40)

Полученное значение 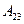подставляем в первое уравнение системы уравнений (2.39) и находим :

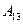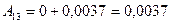(2.41)

Полученные значения 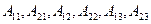подставим в выражение (2.27), где 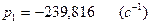(2.18), 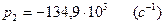(2.19):

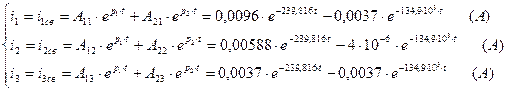(2.42)

Таким образом, переходная характеристика заданного четырехполюсника имеет вид:

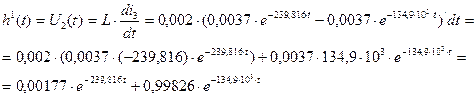(2.43)

2.2 Расчет переходной характеристики цепи операторным методом

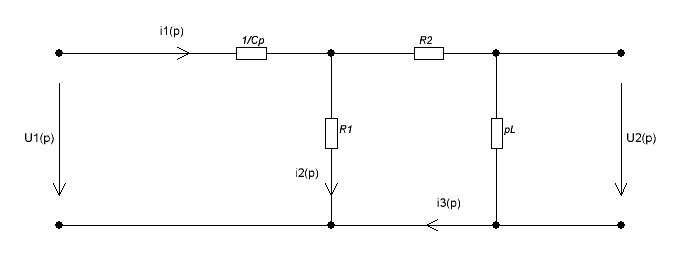
Рисунок 2.3 – Рассчитываемая цепь в операторном виде

На вход рассчитываемой цепи подается напряжение 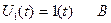, в операторном виде это напряжение будет равно .

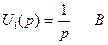Запишем операторное сопротивление цепи:

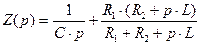(2.44)

Запишем выражение для первого тока 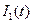в операторном виде:

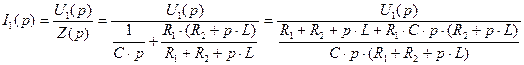
(2.45)

Запишем выражение тока третьего 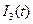через 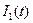в операторной форме:

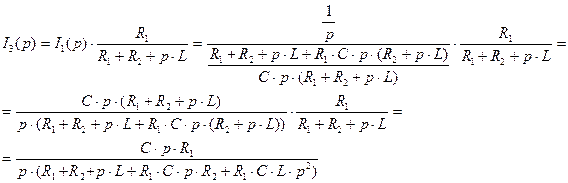
(2.46)

Запишем выражение выходного напряжения 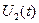в операторном виде:

(2.47)

Обозначим числитель и знаменатель дроби (2.47) соответственно 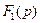и :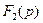

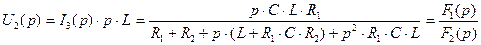(2.48)

Приравниваем знаменатель выражения (2.48) к нулю - 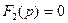и находим корни заданного квадратного уравнения:

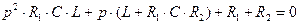(2.49)

Уравнение (2.49) абсолютно совпадает с уравнением (2.14) соответственно корни будут одинаковые:

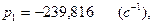(2.16)

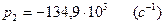(2.17)

Найдем производную от знаменателя дроби (2.48) то есть 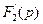: