Марківський процес з дискретними станами і безперервним часом.

На практиці зустрічаються ситуації, коли переходи системи із стану в стан відбуваються не у фіксовані, а у випадкові моменти часу, які заздалегідь вказати неможливо, перехід може здійснитися у будь-який момент. Наприклад, вихід з ладу (відмова) будь-якого елементу апаратури може статися у будь-який момент часу; закінчення ремонту (відновлення) цього елементу також може статися в заздалегідь невідомий момент і т. д.

Для опису таких процесів може бути застосована схема марківського випадкового процесу з дискретними станами і безперервним часом. Такого типу процеси відомі як безперервні ланцюги Маркова. Безперервним ланцюгом Маркова (марківським процесом) називають процес, для якого при
0 ≤ t1≤ t2≤....tn+1 виконується:

P{S(t_n+1) = S_n+1| S(t₁) = S₁,..., S(t_n) = S_n} = P{S(t_n+1) = S_n+1| S(t_n) = S_n}

Тут так само, як і у разі процесу з дискретним часом, розглядається ряд дискретних станів: S₁, S₂, S₃,..., S_n, проте перехід системи S із стану в стан може відбуватися в довільний момент часу.

Позначимо pi(t) - вірогідність того, що у момент t система S знаходитиметься в стані Si (i= 1,..., n). Очевидно, для будь-якого моменту t сума вірогідності станів дорівнює одиниці:

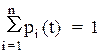(4.5)

оскільки події, що полягають в тому, що у момент t система знаходиться в станах S₁, S₂,..., Sn, неспільні.

Необхідно визначити для будь-кого t вірогідність станів:

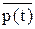= (p₁(t), p₂(t),..., p_n(t))

Для того, щоб знайти цю вірогідність, необхідно знати характеристики процесу, аналогічні перехідній вірогідності для Марківського ланцюга. У разі процесу з безперервним часом замість перехідної вірогідності P_ij розглядається щільність вірогідності (чи інтенсивності) переходу λ _ij (оскільки вірогідність переходу системи із стану в стан точно у момент t дорівнюватиме нулю, так само, як вірогідність будь-якого окремого значення безперервної випадкової величини).

Нехай система S у момент t знаходиться в стані S_r Розглянемо елементарний проміжок часу Δ t, що примикає до моменту t. Назвемо щільністю вірогідності переходу λ _ij із стану i в стан j межа (чи інфінітезимальними коефіцієнтами) відношення вірогідності переходу системи за час Δ t із стану Si в стан Sj до довжини проміжку Δ t:

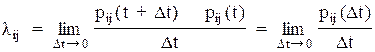(4.7)

де P_ij(Δ t) - вірогідність того, що система, що знаходилася у момент t в стані S_i, за час Δ t перейде з нього в стан S_j (щільність вірогідності переходу визначається тільки для j≠ i). З формули (4.7) витікає, що при малому Δ t вірогідність переходу (з точністю до нескінченно малих вищих порядків) дорівнює:

P_ij(Δ t)=λ _ij Δ t

Якщо уся щільність вірогідності переходу λ _ij не залежить від t (від того, в який момент починається елементарна ділянка Δ t P{S(t + Δ t) = S₁|S(t) = j}, ), марківський процес називається однорідним, а якщо ця щільність залежить від часу, то він є неоднорідним.

Аналіз випадкових процесів з безперервним часом так само як марківських процесів з дискретним часом зручно робити за допомогою графа станів і переходів (рисунок 4.2), на підставі якого можна визначити вірогідність станів р_i(t) (4.6) як функції часу.

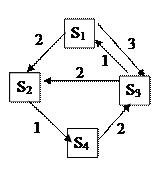
Рисунок - 4.2 Приклад розміченого графа безперервного ланцюга Маркова

Розподіл вірогідності станів системи, яке можна характеризувати вектором 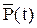= (p₁(t), p₂(t),..., p_n(t)) називається стаціонарним, якщо воно не залежить від часу, тобто усі компоненти вектору 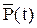є константами.

Вихідними характеристиками марківського процесу з дискретною безліччю станів і безперервним часом є:

- нестаціонарний розподіл вірогідності p_i(t) = P{S(t) = i};

- стаціонарний розподіл вірогідності p_i = 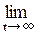p_i(t);

- середній час перебування у фіксованій безлічі станів;

- інтенсивності переходу з однієї безлічі станів в інше.

Дуже важливим є питання про поведінку функцій р₁(t), р₂(t),..., р_n(t) при, t→ ∞, а саме, чи будуть вони прагнути до якихось меж. Якщо ці межі існують, вони називаються граничними (фінальними) вірогідностями станів.

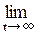p(t) = (p₁, p₂,..., p_n) (4.8)

Очевидно, гранична вірогідність станів в сумі повинна давати одиницю:

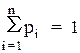(4.9)

Доведено, що якщо число станів системи S кінцеве і з кожного стану можна перейти (за те або інше число кроків) у будь-яке інше, то гранична вірогідність станів існує і не залежить від початкового стану системи.

Таким чином, при t→ ∞, в системі S встановлюється деякий граничний стаціонарний режим: хоча система випадковим чином і міняє свої стани, але вірогідність кожного з них не залежить від часу і кожен із станів здійснюється з деякою постійною вірогідністю, яка є середнім відносним часом перебування системи в цьому стані. Ця властивість дозволяє обходитися при знаходженні параметрів системи на основі моделювання однією досить довгою реалізацією.

Для вірогідності p₁(t), p₂(t),..., p_n(t) можна скласти систему лінійних диференціальних рівнянь, званих рівняннями Колмогорова, які у разі знаходження граничної вірогідності перетворюються на систему лінійних алгебраїчних рівнянь (рівнянь глобального балансу) для кожного стану. Спільно з нормованою умовою (4.9) ці рівняння дають можливість вичислити усі граничні вірогідності (4.8).

Загальне правило складання рівнянь Колмогорова для граничної вірогідності p_i(t) можна сформулювати таким чином:

- в лівій частині рівняння стоїть сума добутків вірогідності усіх станів, з яких йдуть стрілки в i‑ ий стан, на інтенсивності відповідних потоків мінус сума інтенсивностей усіх потоків, що виводять систему з цього (j-го) стану, помножена на вірогідність цього (j-го) стану;

- в правій частині рівняння стоїть 0.

Приклад.

Рівняння для ГСП рисуноку 4.2 матимуть вигляд:

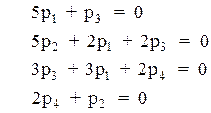
Для отримання системи незалежних рівнянь одно з рівнянь слід замінити на умову нормування (4.9):

р₁+ р₂ + р₃ + р₄ = 1