Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Потік, що входить.

Варіант №1

Варіант №2

Варіант №3

Варіант №4

Варіант №5

Варіант №6

Варіант №7

Варіант №8

Варіант №9

Варіант №10

Варіант №11

Варіант №12

Варіант №13

Варіант №14

Варіант №15

Варіант №16

Варіант №17

3.5 Зміст звіту

Звіт по роботі повинен включати:

- початкові дані по кожному потоку,

- проміжні дані розрахунків,

- значення показників потоків,

- зпостережувані і табличні значення χ 2,

- висновок про прийняття/відкиданні гіпотези пуассонівського (експоненціального) розподілу,

- діаграми теоретичних і експериментальних значень.

3.6 Контрольні запитання і завдання.

1. Що таке пуассонівський потік?

2. Як записується і що дозволяє знайти формула Пуассона?

3. Як називається і що означає параметр пуассонівського закону?

4. Якому закону розподілу підкоряються інтервали між вступом окремих заявок потоку?

5. Чому дорівнює математичне очікування інтервалу часу між подіями в пуассонівському потоці?

6. Чому дорівнює середньоквадратичне відхилення інтервалу часу між подіями в пуассонівському потоці?

7. В яких цілях проводиться апроксимація експериментальних даних відносно потоку заявок і часу обслуговування в системі масового обслуговування теоретичною залежністю?

8. Що буде результатом злиття двох пуассонівських потоків?

9. Які потоки виходять при розгалуженні пуассонівського потоку на декілька потоків?

4. ПОБУДОВА МОДЕЛЕЙ ГИБЕЛІ ТА РОЗМНОЖЕННЯ В ТЕОРІЇ МАСОВОГО ОБСЛУГОВУВАННЯ

4.1 Мета роботи.

Вивчення аналітичних методів опису марківських випадкових процесів.

Дослідження процесів загибелі і розмноження на аналітичній і імітаційній моделі.

4.2 Методичні вказівки з організації самостійної роботи студентів

4.3 Опис методів лабораторної роботи.

Нехай є деяка система S, стан якої змінюється з часом (під системою S може розумітися технічний пристрій, виробничий процес, обчислювальна машина, інформаційна мережа і т. д.). Якщо стан системи S змінюється в часі випадковим, заздалегідь непередбачуваним чином, кажуть, що в системі протікає випадковий процес.

Випадковий процес, що протікає в системі S, називається марківським (чи " процесом без післядії"), якщо він має наступну властивість: для кожного моменту часу t0 вірогідність будь-якого стану системи в майбутньому
(при t > t0) залежить тільки від її стану в сьогоденні (при t = t0) і не залежить від того, коли і яким чином система прийшла в цей стан (тобто як розвивався процес у минулому).

Марківський випадковий процес (ланцюг Маркова) можна визначити також як послідовність випробувань, в кожному з яких з'являється тільки одно з k неспільних подій Ai з повної групи. При цьому умовна вірогідність pij(s) того, що в s -му випробуванні настане подія Aj за умови, що в (s - 1) - ому випробуванні настала подія Ai, не залежить від результатів попередніх випробувань. Незалежні випробування є окремим випадком ланцюга Маркова. Події називаються станами системи, а випробування - змінами станів системи.

Марківські випадкові процеси діляться на класи. Основними класифікуючими ознаками є:

- безліч станів, в яких може знаходитися система;

- моменти часу, в яких відбувається зміна стану системи.

Випадковий процес називається процесом з дискретними станами, якщо можливі стани системи S1, S2, S3,... можна перерахувати (перенумерувати) одно за іншим, а сам процес полягає в тому, що час від часу система S стрибком (миттєво) переходить з одного стану в інше.

Окрім процесів з дискретними станами існують випадкові процеси з безперервними станами: для цих процесів характерний поступовий, плавний перехід із стану в стан. Наприклад, процесом зміни напруги в освітлювальній мережі є випадковий процес з безперервними станами.

Якщо переходи системи із стану в стан можливі тільки в певні моменти часу t1, t2, t3,., то марківський процес відноситься до процесів з дискретним часом. Інакше має місце процес з безперервним часом.

Аналіз випадкових процесів з дискретними станами зазвичай проводиться за допомогою графа станів і переходів (ГСП).

Нехай є система S з n дискретними станами:

S1, S2, S3,..., Sn

Кожен стан зображується прямокутником, а можливі переходи (" перескоки") із стану в стан - стрілками, що сполучають ці прямокутники. Зручно також користуватися розміченим графом, який графічно зображує не лише можливі стани системи і можливі переходи із стану в стан, але також і значення вірогідності переходу.

Приклади ГСП показані на рисунку 4.1

Рисунок 4.1 - Приклади графа станів і переходів

Системі графу, що містить n вершин, можна поставити у відповідність матрицю n × n, елементами якої є вірогідність переходів pij між вершинами графа, що зветься матрицею вірогідності переходів. Елементи матриці p_ij задовольняють умовам:

0 ≤ p_ij ≤ 1 (4.1)

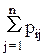= 1 (4.2)

Умова (4.1) - звичайна властивість вірогідності, а умова (4.2) означає, що система S обов'язково або переходить з якогось стану Si в інший стан, або залишається в стані Si. Елементи p_ij матриці P означають вірогідність переходів в системі за один крок.

Зазвичай на графі вірогідності переходу системи з одного стану в те ж саме не відзначаються. При розгляді конкретних систем зручно спочатку побудувати граф станів, потім визначити вірогідність переходів системи з одного стану в те ж саме (виходячи з вимоги рівності одиниці суми елементів рядків матриці), а потім скласти матрицю переходів системи.

Нехай система S може знаходитися в станах:

S1, S2, S3,..., Sn

і зміни стану системи можливі тільки в моменти:

t1, t2, t3,..., tn

Називатимемо ці моменти кроками, або етапами процесу і розглядатимемо той, що протікає в системі S випадковий процес як функцію цілочисельного аргументу m = 1, 2,... k,...,, що означає номер кроку.

Вказаний випадковий процес полягає в тому, що в послідовні моменти часу t1, t2,..., tk,... система S опиняється в тих або інших станах. Процес, що відбувається в системі, можна представити як послідовність (ланцюжок) подій, наприклад:

,

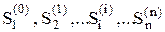що зветься марківським ланцюгом, де для кожного кроку вірогідність переходу з будь-якого стану Si у будь-яке Sj не залежить від того, коли і як система прийшла в стан Si.

Марківський ланцюг можна описати за допомогою вірогідності станів, в якій знаходиться система на якомусь кроці. Нехай у будь-який момент часу (після будь-якого кроку) система може перебувати в одному із станів:

S₁, S₂, S₃,..., S_n

тобто в результаті кроку k здійсниться одно з повної групи неспільних подій:

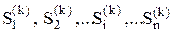
Позначивши вірогідність цих подій для k -го кроку через:

p₁(k) = p(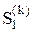), p₂(k) = p(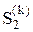),..., p_i(k) = p(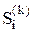),..., p_n(k) p()

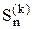легко бачити, що для кожного кроку k:

p₁(k) + p₂(k) +...+ p_i(k) +... + p_n(k) = 1

оскільки 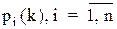, є вірогідність появи повної групи подій.

Вірогідності 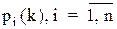називається вірогідностями стану.

Для будь-якого кроку (моменту часу t₁, t₂,..., t_k,... чи номери 1, 2,..., k,...) існує деяка вірогідність переходу системи з будь-якого стану у будь-яке інше (деякі з них дорівнюють нулю, якщо безпосередній перехід за один крок неможливий), а також вірогідність затримки системи в цьому стані. Ці вірогідності називаються перехідними вірогідностями марківського ланцюга.

Якщо значення перехідної вірогідності не залежать від номера кроку, то марківський ланцюг називається однорідним, або стаціонарним. Інакше марківський ланцюг є неоднорідним, або нестаціонарним.

Для графа (рисунок 4.1) значення перехідної вірогідності будуть дорівнювати:

P₁₁ = 1 – (P_{12 +} P₁₃)

P₂₂ = 1 – (P₂₃ + P₂₄ + P₂₅)

P₃₃ = 1

P₄₄ = 1 – P₄₅

P₅₅ = 1 – P₅₃

Якщо із стану Si не виходить жодної стрілки (перехід з нього ні в який інший стан неможливий), відповідна вірогідність затримки Рii дорівнює одиниці.

Маючи в розпорядженні розмічений ГСП (чи, що рівносильно, матрицю перехідної вірогідності) і знаючи початковий стан системи, можна знайти вірогідність станів р₁(k), р²(k),..., рⁿ(k) після будь-якого (k-го) кроку. Вони знаходяться за допомогою наступних рекурентних співвідношень:

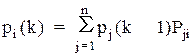(i = 1,..., n) (4.3)

чи в матричній формі

p^(k) = p^(k-1) × P (4.4)